Общая схема определения линейных и сдвиговых деформаций.

Деформация любого элементарного объема тела (параллелепипед), может быть представлена из ряда отдельных простейших деформаций, т.е. разложена на составляющие. Имеется шесть составляющих деформаций: три линейных (удлинений) и три угловых (сдвиги). Линейные деформации обозначаются 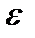с индексом, указывающим направление удлинения. Положительной деформацией считается деформация удлинения. При данных деформациях изменяется объем и форма.

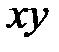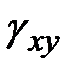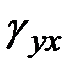Положительному сдвигу соответствует уменьшение угла между направлением осей. Углы сдвига (относительные сдвиги), проектирующиеся на плоскость , обозначаются или , рис. 4.2. Для других плоскосте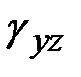й - или 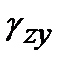и т. д. Считается, что при малых углах сдвига, объем остается неизменным. Угловые деформации не влияют на линейные.

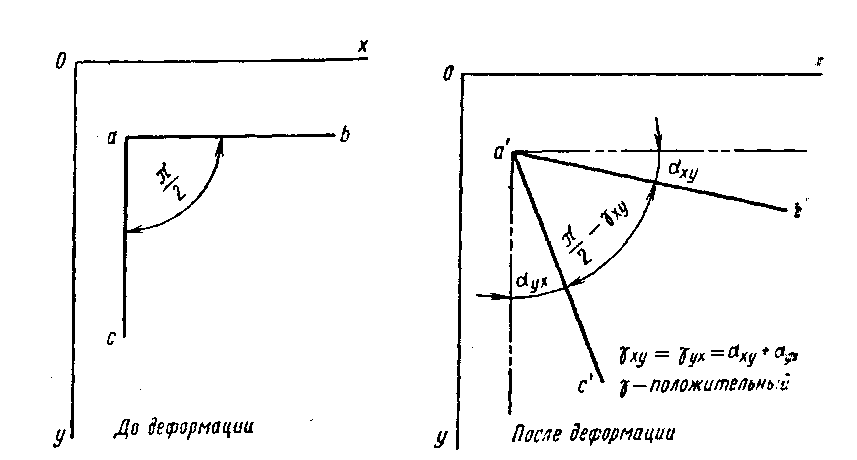
Рисунок 4.2 - Угловые деформации

Выразим компоненты деформаций через компоненты перемещений. Выделим в точке тела элементарный объем с бесконечно малыми ребрами 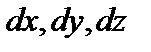, параллельными осям координат. Проекция элементарного параллелепипеда на плоскость 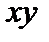до деформации, точка 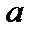является проекцией рассматриваемой точки 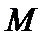на плоскость, рис. 4.3.

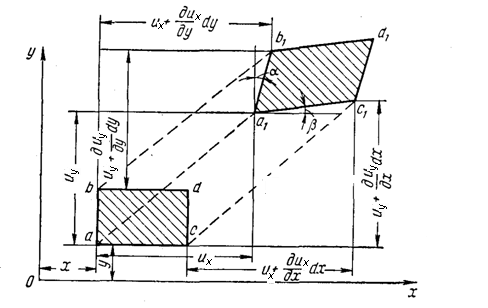
Рисунок 4.3 - Перемещения точки в плоскости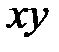

После деформации точки получили перемещения, и перешли в положение со штрихом. В общем, все перемещения зависят от координат, при этом необходимо учитывать перемещения связанные и с пластической деформацией. Если перемещения вдоль соответствующих осей зависят и от производных по этим же координатам, то пластическое течение совпадает с общим перемещением точки. Если нет, то пластическое течение перпендикулярно общему перемещению и тогда появляются сдвиги. В первом случае:

,

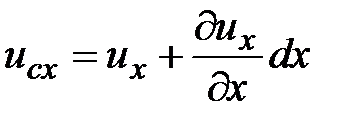где 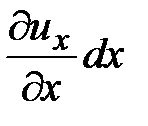- удлинение ребра в результате его деформации вдоль оси .

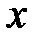Относительная деформация:

.

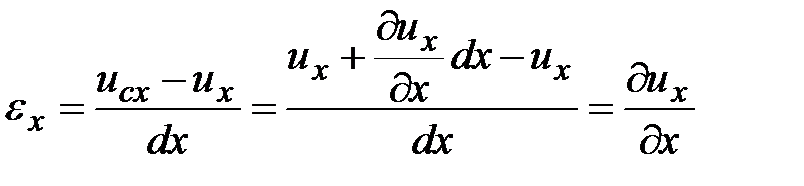Аналогично получим:

,

.

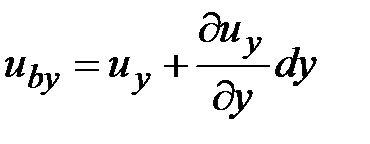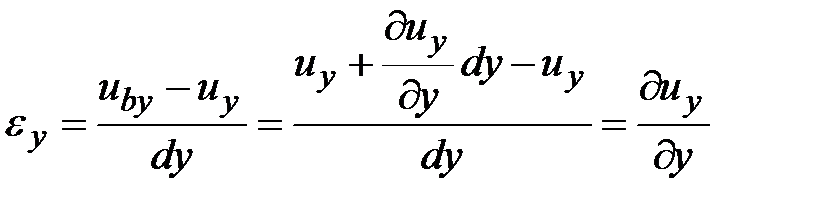Во втором случае:

; ,

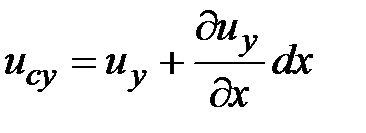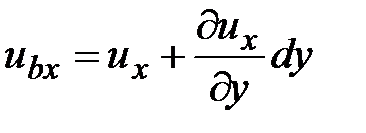где 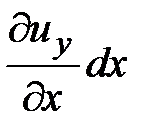и 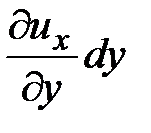- смещение векторов перемещени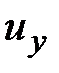й и 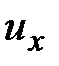в поперечном направлении 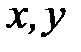, что приводит к угловым сдвигам 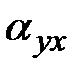и 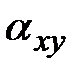. Если их нет, смещаемые точки располагаются на прямых параллельных осям координат. Частные производные становятся равными нулю. Принимая 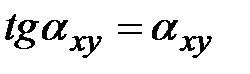и 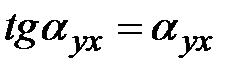, запишем:

.

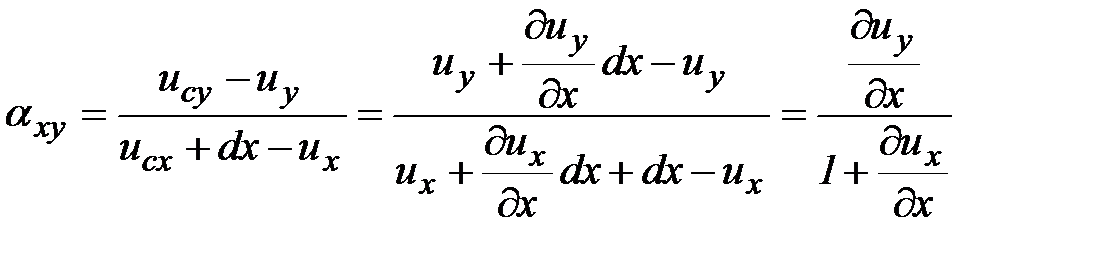Так как 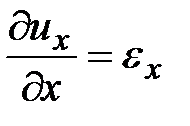значительно меньше единицы, то 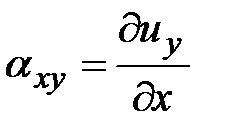. Тем же способом получим 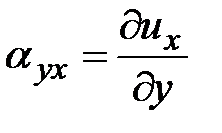. Тогда 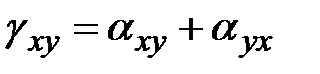. Следовательно:

.

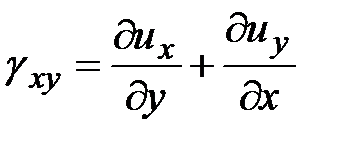Принято выражать сдвиги в виде половинок, тогда 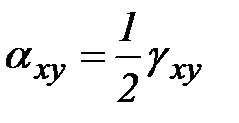, 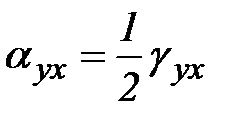. Причем 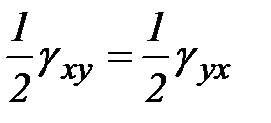. Индексация будет совпадать с индексацией касательных напряжений и касательных перемещений в предыдущем разделе. В итоге получим: относительные удлинения:

, , ,

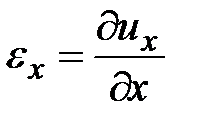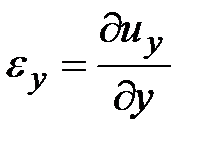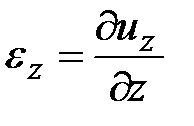относительные сдвиги:

, , .

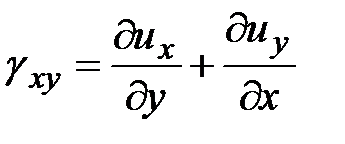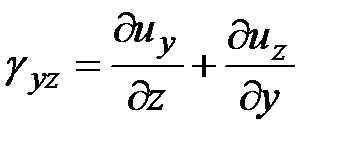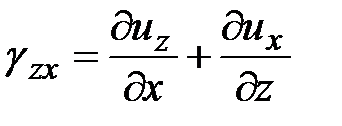Эти уравнения получим О.Л. Коши. Линейные и сдвиговые деформации можно записать в виде таблицы:

.

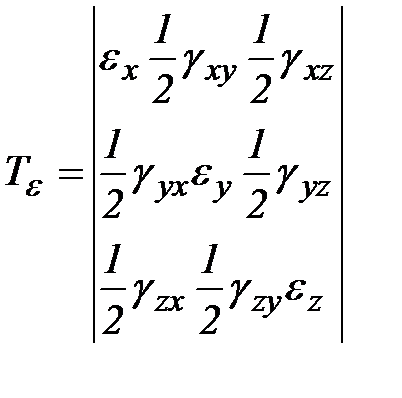Значение 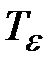является тензором деформаций, обладающий такими же свойствами, как и тензор напряжений. Он полностью определяет деформированное состояние точки.

Из последних соотношений определим элементарные перемещения точек в результате пластической деформации, тогда:

,

.

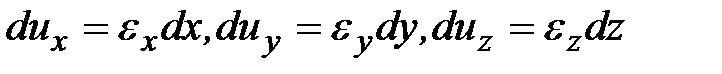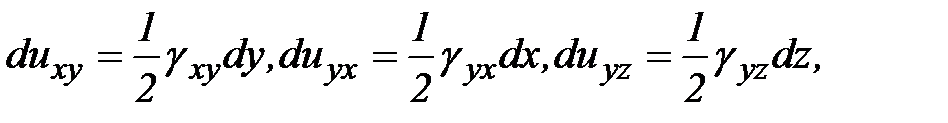
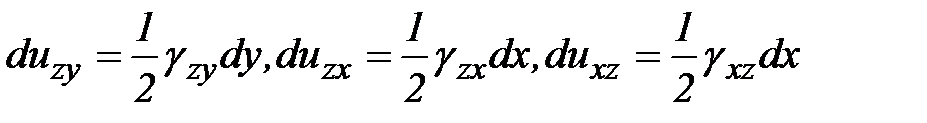Если подставить последние соотношения в выражение для определения приращения вектора перемещения с учетом, что 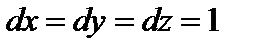, тогда:

,

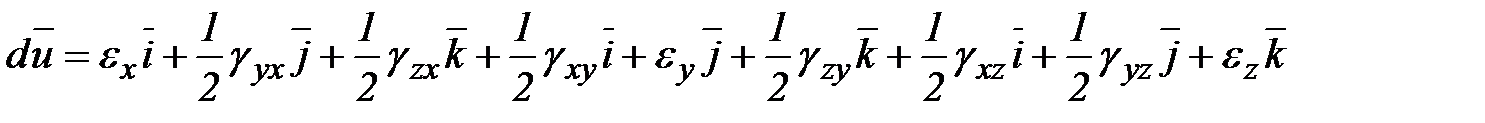или

.

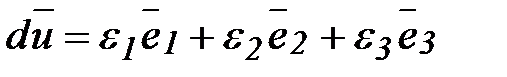Для осесимметричного напряженного состояния в цилиндрических координатах без вывода:

, , , .

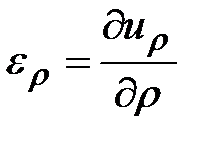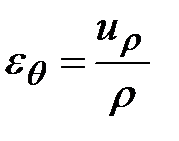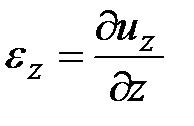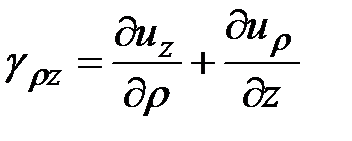Следует подчеркнуть, что пластической деформации в направлении координаты 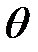нет. Деформация 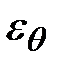определяется геометрическими построениями.

Можно показать, что в цилиндрических координатах при объемном напряженно-деформированном состоянии компоненты тензора деформаций имеют вид:

, , ,

, .

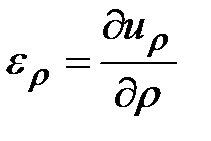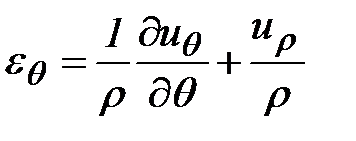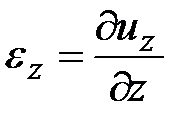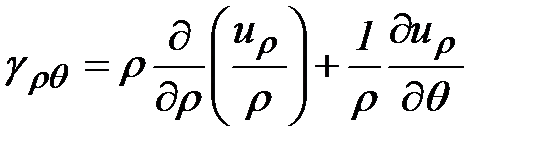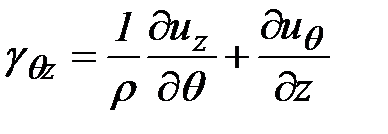
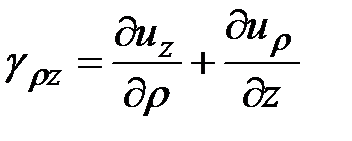На границе перемещение 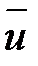можно представить в виде:

,

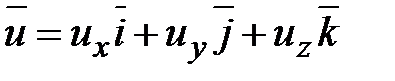не раскладывая предварительно на составляющие по главным направлениям.