Дифференциальные уравнения равновесия объемного напряженного состояния точки.

Математические модели процессов, явлений описываются дифференциальными уравнениями, которые выводятся из фундаментальных законов природы. В механике на основе условий равновесия или движения.

Напряжения являются непрерывными функциями координат. Выделим в напряженном теле элементарный параллелепипед, рис. 3.6. Напряженное состояние в точке 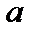определяется тензором напряжений:

.

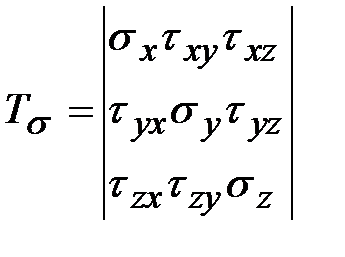Напряжения в точке 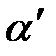отличается от напряжений в точке 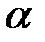на бесконечно малую величину. В общем случае для нормального напряжения вдоль оси

.

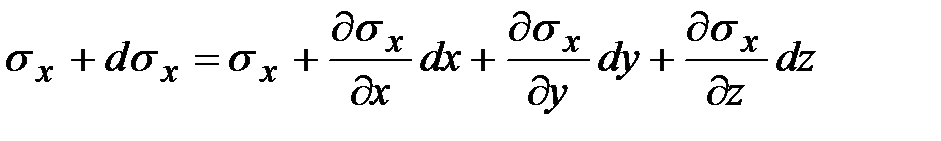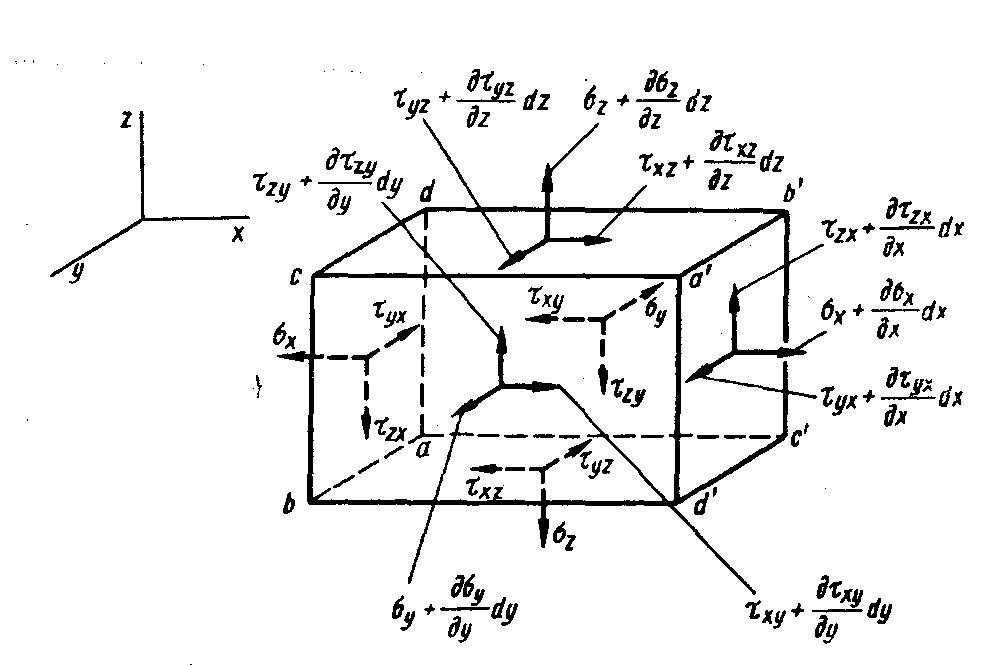
Рисунок 3.6 - Равновесие элементарного параллелепипеда

Однако если нет смещения точек относительно оси координат 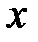, то можно записать 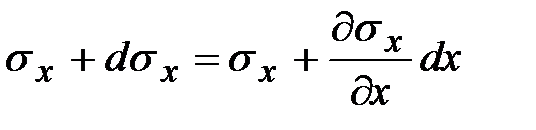. Последнее утверждение позволяет упростить решение задачи. Отсюда тензор напряжений:

.

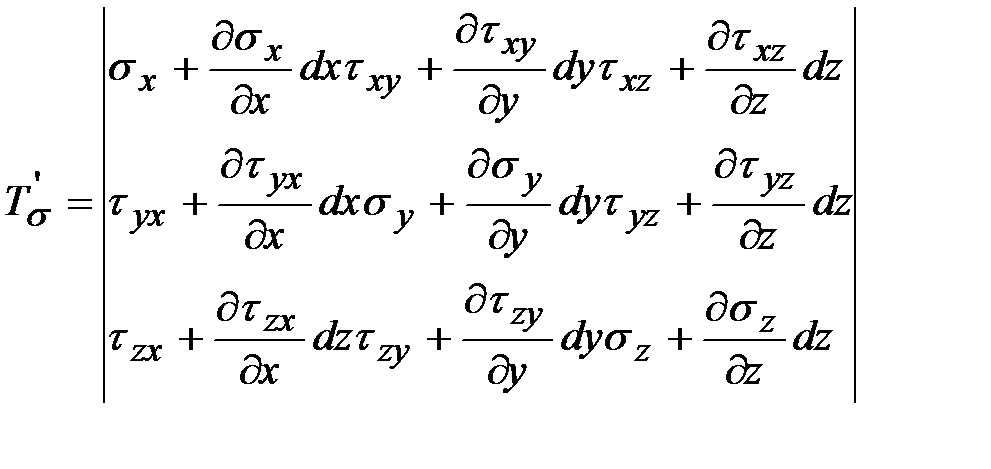Условие равновесия элементарного объема определяется уравнениями равновесия.

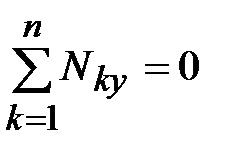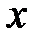Алгебраические суммы проекций всех сил на оси координат должны быть равны нулю, т.е. , , . Составляя уравнение равновесия сил на ось имеем:

.

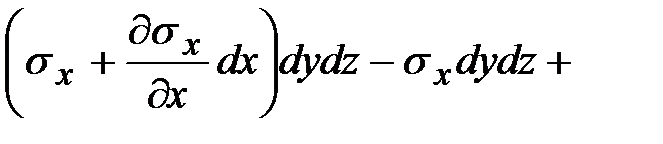
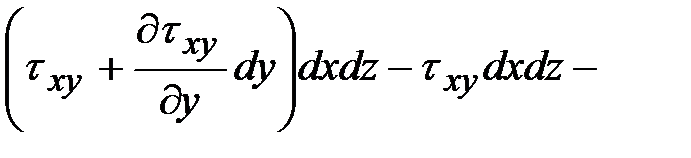
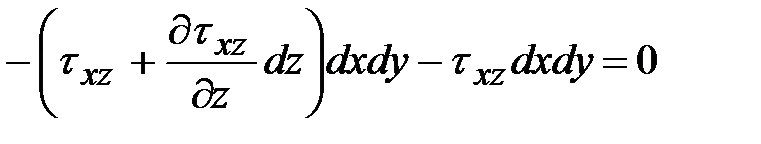Раскрывая скобки и сокращая на 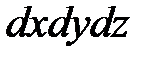, получим:

.

Аналогично уравнения равновесия на оси и . В итоге :

;

;

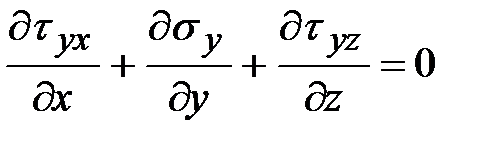Представленные выражения определяют собой дифференциальные уравнения в частных производных и являются условиями равновесия для объемного напряженного состояния. Эти условия обязательны для всех точек деформируемого тела.

Если на тело действуют массовые силы и пластическая деформация испытывает динамическое воздействие, тогда уравнения движения среды:

;

;

.

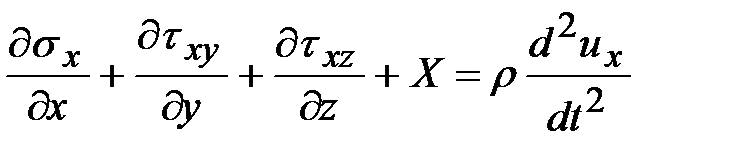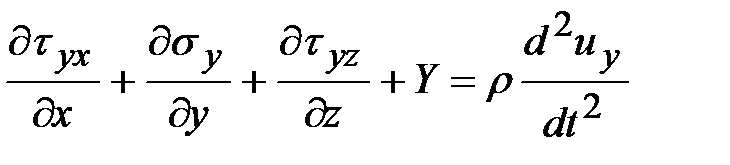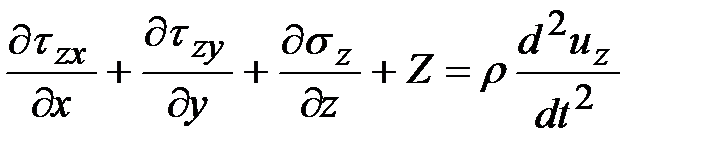где 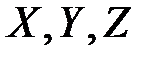- массовые силы, действующие на элементарный объем;

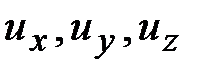- перемещения частиц среды вдоль осей координат .

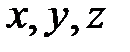Напряжения меняются по объему тела, и в элементах, выходящих на поверхность. Их величина должна быть такой, чтобы уравновесить внешнюю нагрузку, т.е. удовлетворить условиям на контуре.

Частным случаем объемного напряженного состояния является осесимметричное напряженное состояние. Оно относится к телам вращения. Внешние нагрузки расположены симметрично относительно оси и одинаковы во всех меридиональных сечениях. Это осадка цилиндрической заготовки, прошивка, прессование, волочение и т.д. В этом случае используют цилиндрическую систему координат ( 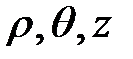). Напряжения в цилиндрических координатах, рис. 3.7.

Тензор напряжений:

.

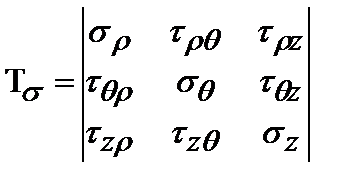При осесимметричном напряженном состоянии компоненты напряжений не зависят от координаты 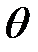. В плоскости 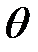. не возникает касательных напряжений, вследствие симметрии тела и нагрузок, поэтому:

.

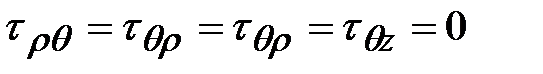Следовательно, 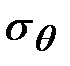будет главным напряжением. Тензор напряжений при осесимметричном напряженном состоянии :

.

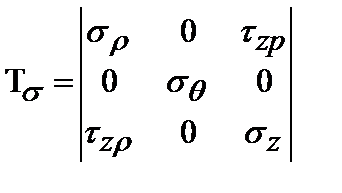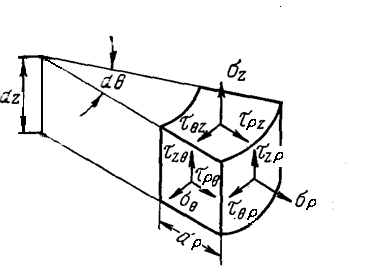
Рисунок 3.7 - Напряжения в цилиндрических координатах

Принимая тот же метод сечений, запишем условие равновесия сил на ос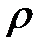и и 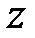, принимая при этом 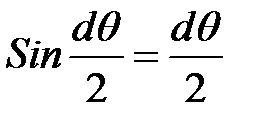, тогда:

.

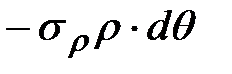
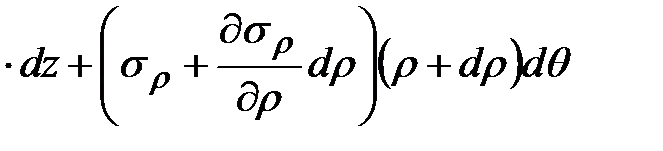
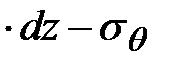
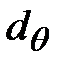
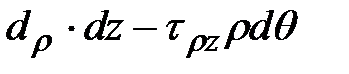
Аналогично проектируя на ось 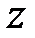и, после несложных преобразований и сокращений, получим:

; .

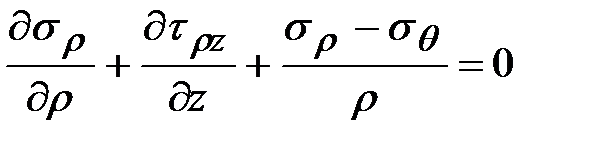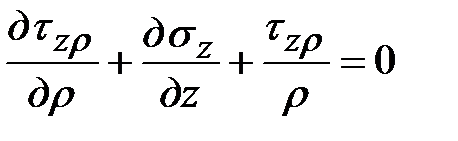При решении некоторых задач касательные напряжения могут отсутствовать. В этом случае вместо двух уравнений равновесия остается одно:

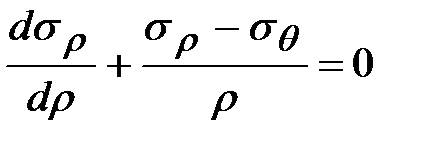
Нормальные напряжения здесь являются главными.

Плоская задача теории пластичности, декартовая система координат. Плоское напряженное состояние или плоско деформированное. Касательные напряжения с нижним индексом координаты, вдоль которой отсутствует компонент напряжения или деформации, равны нулю. Например, 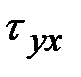и 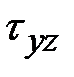, тогда:

; .

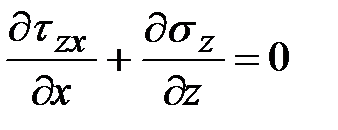В полярных координатах, уравнения равновесия плоской задачи:

;

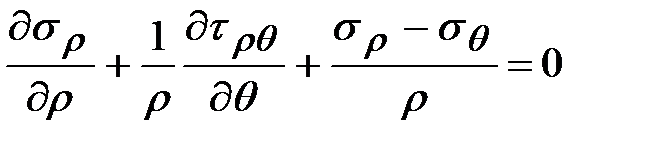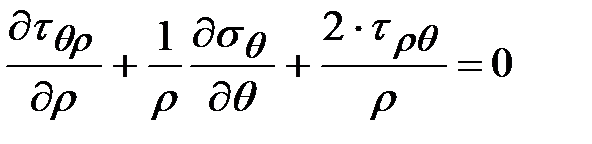
Возвращаясь к объемному напряженному состоянию для цилиндрических координат можно записать:

;

;

.

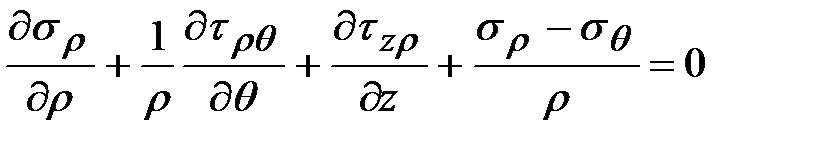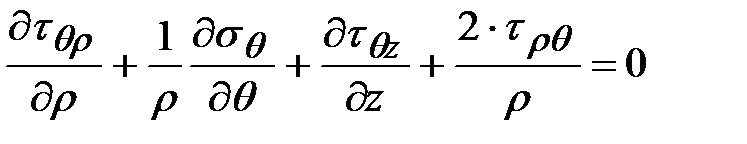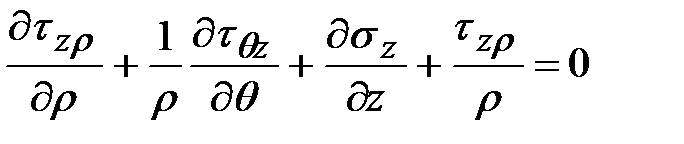Из сопоставления видно, что вид дифференциальных уравнений равновесия зависит от выбранных систем координат.