Потенциометрические схемы
3.2.1. Схемы с резистивными датчиками
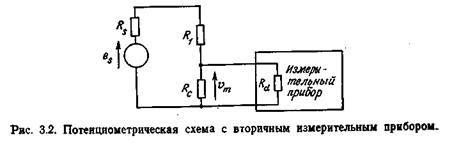
Датчик с изменяющимся сопротивлением Rc, включенный последовательно с резистором постоянного сопротивления R1, питается источником с внутренним сопротивлением Rs, э.д.с. еs которого постоянна или переменна (рис. 3.2). Выходное напряжение νm, измеряемое на выходе датчика прибором с входным сопротивлением Rd , равно
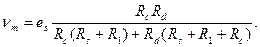
Напряжение на выходе датчика не зависит от используемого измерительного прибора при Rd>>Rc, в этом случае оно равно
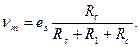
и является нелинейной функцией Rс.
|
Линеаризация измерений. Желательно, чтобы вариации 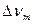 измеряемого напряжения были пропорциональны вариациям ΔRc сопротивления датчика.
измеряемого напряжения были пропорциональны вариациям ΔRc сопротивления датчика.
Работа на малом участке характеристики. Сопротивление датчика меняется от Rc0 до Rc0 +ΔRc вызывая изменения напряжения 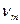 от
от 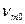 до
до 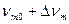
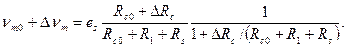
При условии ΔRc<<Rc0+R1+Rs с точностью до малых величин второго порядка имеем
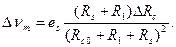
Чувствительность схемы формирования Δνm/ΔRc максимальна, если выбрать Rs+R1=Rc0, в этом случае
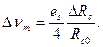
Если внутреннее сопротивление источника Rs мало, то чувствительность максимальна на относительно большом участке характеристики, что подтверждается предыдущей формулой, поскольку в этом случае с хорошим приближением можно полагать, что R1≈Rc0.
Питание схемы источником тока. Внутреннее сопротивление источника Rs очень велико: Rs >>Rc0+R1. В этом случае должно выполняться условие ΔRc<<Rc0+R1+Rs. Подставляя is=es/Rs, получим 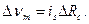
|
|
Исключение постоянной составляющей из выходного сигнала. Недостатком рассмотренной потенциометрической схемы является наличие в выходном сигнале постоянной составляющей, не содержащей полезной информации. Относительно большое значение этой составляющей требует использования вольтметров с неоправданно широким диапазоном измерений. Нередко это приводит к увеличению погрешности измерений и, во всяком случае, к неэффективному использованию измерительных средств.
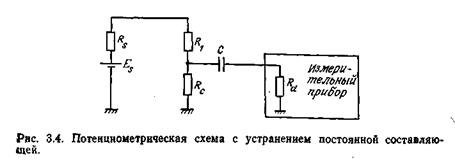
Для выделения полезной (переменной) составляющей сигнала можно использовать емкостную связь между датчиком и вольтметром, как это показано на рис. 3.4. Конденсатор С и внутреннее сопротивление Rd вольтметра образуют фильтр верхних частот.
Если 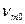 — постоянная составляющая напряжения на выходе схемы, то фильтр верхних частот позволяет отделить переменную составляющую
— постоянная составляющая напряжения на выходе схемы, то фильтр верхних частот позволяет отделить переменную составляющую 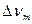 от
от 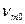 . Необходимо лишь, чтобы нижняя граничная частота фильтра
. Необходимо лишь, чтобы нижняя граничная частота фильтра 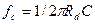 была меньше самой низкой частотной составляющей измеряемой величины. Обычно для устранения постоянной составляющей используют мостовую схему, представляющую собой двойной потенциометр, и потенциометрическую схему с симметричным питанием.
была меньше самой низкой частотной составляющей измеряемой величины. Обычно для устранения постоянной составляющей используют мостовую схему, представляющую собой двойной потенциометр, и потенциометрическую схему с симметричным питанием.
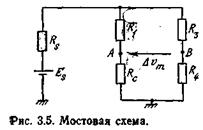
В мостовой схеме, представленной на рис. 3.5, параллельно сопротивлениям R1 и Rc включают сопротивления R3 и R4, которые здесь предполагаются постоянными. Эти сопротивления выбирают такими, чтобы относительно массы потенциал в точке В равнялся 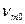 , потенциал в точке А был бы равен
, потенциал в точке А был бы равен 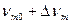 , а измеряемое между точками А и В выходное напряжение было бы равно
, а измеряемое между точками А и В выходное напряжение было бы равно 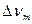 .
.
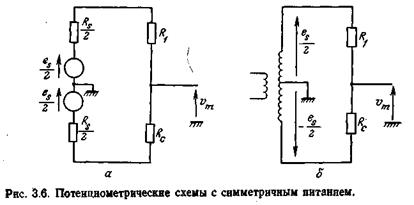
Условием равенства потенциала в точке В значению ото является соотношение
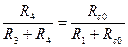 , откуда
, откуда 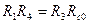 .
.
Это условие равновесия моста Уитстона, который детально описан в разд. 3.3.1.
Потенциометрические схемы с симметричным питанием представлены на рис. 3.6.
Выходное напряжение 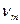 , измеряемое относительно массы определяется выражением
, измеряемое относительно массы определяется выражением
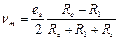 .
.
Выбирая R1 равным сопротивлению датчика Rc0 при Um=Um0,. т. е. до начала воздействия измеряемой величины, и полагая Rs<<Rc0, при Rc=Rc0+ΔRc получим
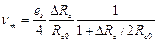 , т. е. выходное напряжение не содержит постоянной составляющей.
, т. е. выходное напряжение не содержит постоянной составляющей.
Влияние нестабильности напряжения питания. Это влияние сказывается на изменении чувствительности потенциометрических схем. В схеме с несимметричным питанием (см. рис. 3.7, а) флуктуации Δе напряжения еs0 приводят в процессе измерений к приращениям выходного сигнала (с погрешностью до величины второго порядка значимости)
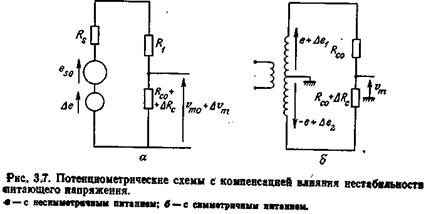
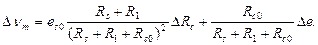
При этом трудно выделить приращения, обусловленные отдельно изменениями 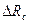 и
и 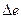 .
.
В схеме с симметричным питанием (рис. 3.7,6) следует учитывать два влияющих воздействия — 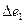 и
и 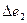 — на приращения измерительного сигнала напряжения (с точностью до малых второго порядка)
— на приращения измерительного сигнала напряжения (с точностью до малых второго порядка)
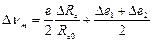 .
.
Кроме частного случая, когда 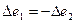 , невозможно выделить полезную составляющую выходного сигнала, связанную только с изменением
, невозможно выделить полезную составляющую выходного сигнала, связанную только с изменением 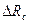
3.2.2. Измерительные схемы с индуктивными и емкостными датчиками
Пусть датчик с импедансом 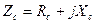 включен последовательно с импедансом
включен последовательно с импедансом 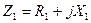 в цепь с источником синусоидальной э.д.с.
в цепь с источником синусоидальной э.д.с. 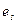 , внутренний импеданс источника предполагается пренебрежимо малым. Рассмотрим особенности измерительных схем в зависимости от соотношений
, внутренний импеданс источника предполагается пренебрежимо малым. Рассмотрим особенности измерительных схем в зависимости от соотношений 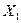 и
и 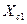 .
.
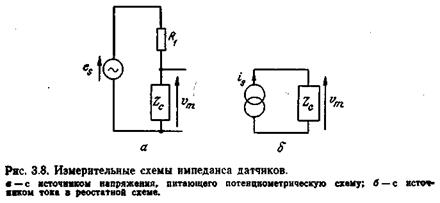
1. 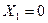 . В этом случае импеданс
. В этом случае импеданс 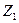 представляет собой постоянноеактивное сопротивление
представляет собой постоянноеактивное сопротивление 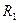 (рис. 3.8, с). Когда импеданс датчика изменяется от
(рис. 3.8, с). Когда импеданс датчика изменяется от 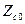 до
до 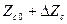 напряжение на его клеммах меняется на
напряжение на его клеммах меняется на 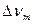 :
:
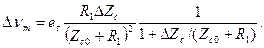
При выборе 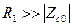 предыдущее выражение упрощается, т.е.
предыдущее выражение упрощается, т.е.
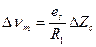 ,
,
и через импеданс 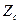 протекает постоянный ток
протекает постоянный ток 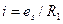 .
.
Это означает возможность замены источника напряжения 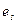 источником тока
источником тока 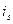 и отказ от сопротивления
и отказ от сопротивления 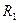 (рис. 3.8,6); тогда вариации выходного напряжения составят
(рис. 3.8,6); тогда вариации выходного напряжения составят 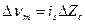 .
.
2. 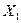 и
и 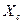 изменяются в одном направлении. Рассмотрим схему на рис. 3.9, а, образованную двумя датчиками
изменяются в одном направлении. Рассмотрим схему на рис. 3.9, а, образованную двумя датчиками 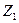 и
и 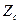 .
.
В отсутствие измеряемой и влияющей величин импедансы датчиков равны 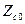 .
.
При воздействиях этих величин импедансы датчиков изменяются, причем
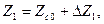
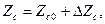
где 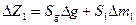 и
и 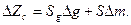
Здесь 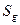 — чувствительность, характеризующая воздействие на
— чувствительность, характеризующая воздействие на 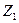 и
и 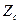 .влияющей величины при изменении ее на
.влияющей величины при изменении ее на 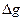 ;
; 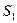 и
и 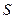 — чувствительности соответствующих датчиков при изменениях измеряемой величины соответственно на
— чувствительности соответствующих датчиков при изменениях измеряемой величины соответственно на 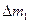 и
и 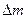 .
.
Выходное напряжение при этом равно 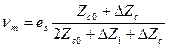
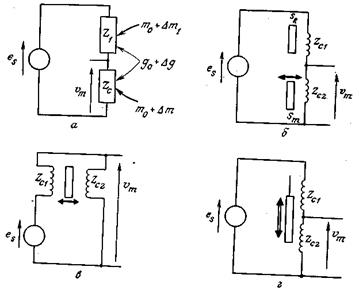
Рис. 3.9. Потенциометрические схемы с дифференциальным включением идентичных датчиков. а – принципиальная схема; б – датчик расстояния, использующий токи Фуко с компенсацией влияющей величины ( 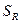 -неподвижная металлическая поверхность,
-неподвижная металлическая поверхность, 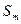 - подвижная поверхность); в – датчик типа б с дифференциальным включением; г – датчики перемещения с дифференциальным включением.
- подвижная поверхность); в – датчик типа б с дифференциальным включением; г – датчики перемещения с дифференциальным включением.
а его изменение относительно начального значения 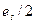 составляет
составляет 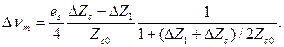
Если датчик с импедансом 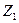 играет только роль компенсатора влияющей величины, то
играет только роль компенсатора влияющей величины, то
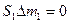 , а
, а 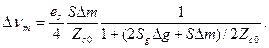
Когда 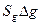 и
и 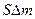 оказываются существенно меньше
оказываются существенно меньше 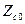 , то с точностью до малых величин второго порядка можно записать, что
, то с точностью до малых величин второго порядка можно записать, что 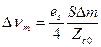 .
.
Для случая взаимно обратных реакций датчиков на одно и то же воздействие измеряемой величины
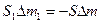
имеем 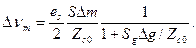
Сигнал 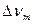 в этом случае дифференциального включения датчиков является линейной функцией приращения измеряемой величины, и когда
в этом случае дифференциального включения датчиков является линейной функцией приращения измеряемой величины, и когда 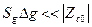 , то
, то 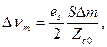
т. е. исключается также и влияющее воздействие. Такое включение целесообразно только для индуктивных датчиков с подвижным сердечником, предназначенных для измерения перемещений и расстояния (рис. 3.9,б, в, г).
При включении в потенциометрическую схему емкостного датчика возникает погрешность, вызванная наличием паразитных емкостей, образуемых каждой пластиной конденсатора (датчика) с массой. Действительно, как видно на рис. 3.10, а, паразитные емкости 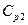 и
и 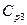 включены параллельно емкости датчика и их изменения неотличимы от изменений емкости датчика, а емкость
включены параллельно емкости датчика и их изменения неотличимы от изменений емкости датчика, а емкость 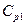 включена параллельно источнику и ее влияние пренебрежимо мало (если емкостное сопротивление
включена параллельно источнику и ее влияние пренебрежимо мало (если емкостное сопротивление 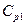 велико по сравнению с импедансом источника).
велико по сравнению с импедансом источника).
В этом случае вместо потенциометрической лучше применять гальванометрическую схему, представленную на рис. 3.10,б. В этой схеме измеряется ток 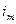 , который определяют с помощью прибора с очень малым входным сопротивлением
, который определяют с помощью прибора с очень малым входным сопротивлением 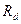 . Паразитная емкость, параллельная
. Паразитная емкость, параллельная 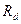 , на погрешность измерений оказывает пренебрежимо малое влияние.
, на погрешность измерений оказывает пренебрежимо малое влияние.
Пренебрегая значением 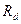 , измеряемый ток можно выразить формулой
, измеряемый ток можно выразить формулой 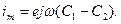
Если 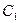 — емкость датчика:
— емкость датчика: 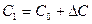 и
и 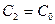 , то
, то 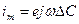 .
.
В качестве примера работы двух включенных дифференциально конденсаторных датчиков 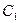 и
и 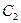 рассмотрим:
рассмотрим:
а) датчики перемещения с изменяющейся площадью поверхности пластин 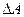 (см. разд. 7.3.2), для которых
(см. разд. 7.3.2), для которых
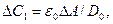
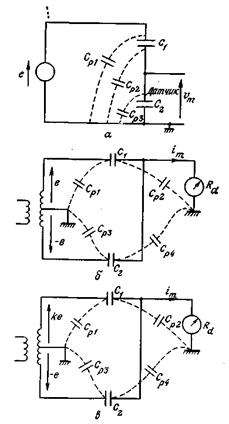
Рис. 3.10. Измерительные схемы с емкостным датчиком.
а – потенциометрическая; б – гальванометрическая; в – гальванометрическая с трансформатором питающего напряжения с переменным коэффициентом трансформации.
откуда 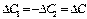 и
и 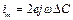 , т.е. следует, что схема линейна;
, т.е. следует, что схема линейна;
б) датчики перемещения с изменяющимся расстоянием между пластинами конденсатора (см. разд. 7.3.3), для которых
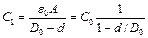 ,
, 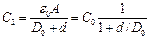 ,
,
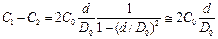 при
при 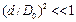
и 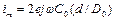 , откуда следует, что схема квазилинейна для небольших перемещений.
, откуда следует, что схема квазилинейна для небольших перемещений.
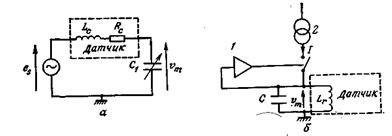
Рис. 3.11. Частотно-задающие контуры с индуктивными датчиками.
а — последовательная схема; 6 — параллельный контур (Е1есtго-Согрогаtion). 1 - управляемый контакт; 2 — источник постоянного тока.
Гальванометрические схемы в общем случае включают и трансформатор отношений (рис. 3.10,в): амплитуды напряжений на каждом выходе находятся в соотношении 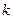 , точно определяемом положением отвода на землю. В этом случае измеряемый ток равен:
, точно определяемом положением отвода на землю. В этом случае измеряемый ток равен:
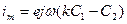 .
.
Если 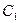 — емкость
— емкость 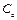 переменного опорного конденсатора и
переменного опорного конденсатора и 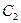 — емкость датчика
— емкость датчика 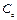 , то эту последнюю можно определить с большой точностью по исчезновению измеряемого тока, наступающему при условии
, то эту последнюю можно определить с большой точностью по исчезновению измеряемого тока, наступающему при условии 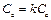 .
.
3. 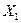 и
и 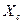 имеют противоположные знаки. Пусть
имеют противоположные знаки. Пусть 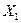 — емкостное сопротивление конденсатора
— емкостное сопротивление конденсатора 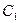 переменной емкости с воздушным диэлектриком (рис. 3.11.а). Напряжение на конденсаторе в этом случае определяется как
переменной емкости с воздушным диэлектриком (рис. 3.11.а). Напряжение на конденсаторе в этом случае определяется как
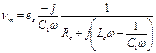 .
.
При изменении емкости переменного конденсатора 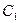 возникает резонанс, при котором максимальная амплитуда напряжения на конденсаторе равна
возникает резонанс, при котором максимальная амплитуда напряжения на конденсаторе равна
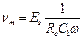 .
.
Здесь 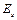 — амплитуда источника; отсюда следует, что
— амплитуда источника; отсюда следует, что
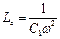 ,
, 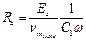 .
.
На рис. 3.11,б представлена схема, в которой катушка датчика с индуктивностью 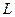 и сопротивлением
и сопротивлением 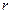 образует с постоянным конденсатором
образует с постоянным конденсатором 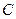 параллельный колебательный контур, резонансная частота которого
параллельный колебательный контур, резонансная частота которого
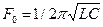
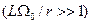 .
.
Контур возбуждается источником постоянного тока 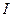 , прерываемым с частотой
, прерываемым с частотой 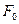 управляемым контактом; при этом напряжение на колебательном контуре равно
управляемым контактом; при этом напряжение на колебательном контуре равно 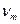 . Учитывая резонансное свойство контура, его можно рассматривать как возбуждаемый синусоидальным сигналом на частоте
. Учитывая резонансное свойство контура, его можно рассматривать как возбуждаемый синусоидальным сигналом на частоте 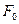 , а сила протекающего через него тока
, а сила протекающего через него тока 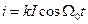 , где
, где 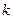 (
( 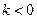 ) зависит от скважности тока прерывателя. При этих условиях напряжение
) зависит от скважности тока прерывателя. При этих условиях напряжение 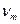 на зажимах контура будет иметь амплитуду
на зажимах контура будет иметь амплитуду
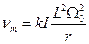 .
.
Такая схема позволяет обойтись без источника с регулируемой частотой, так как возбуждение схемы на соответствующей частоте происходит автоматически.
3.2.3. Недостатки потенциометрической схемы
Основные трудности использования потенциометрической схемы связаны с опасностью изменения чувствительности из-за дрейфа источников питания и паразитных влияний.
Несимметричное питание (рис. 3.11,а). При одновременном изменении в электрической цепи сопротивления датчика 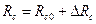 и флуктуации напряжения источника
и флуктуации напряжения источника 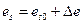 вариация
вариация 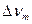 измеряемого напряжения с точностью до малых второго порядка равна
измеряемого напряжения с точностью до малых второго порядка равна
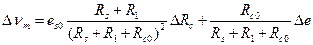 .
.
Очевидно, трудно заранее определить составляющие 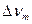 , ответственные за
, ответственные за 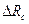 и
и 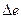 .
.
Симметричное питание (рис. 3.11,б). В этом случае нужно рассмотреть паразитные влияния на 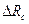 отклонений
отклонений 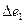 и
и 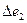 , индуцированных в двух ветвях источника; при этом общая вариация измеряемого напряжения с точностью до малых второго порядка определяется выражением
, индуцированных в двух ветвях источника; при этом общая вариация измеряемого напряжения с точностью до малых второго порядка определяется выражением
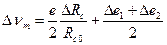 .
.
Вариацию, связанную только с изменением 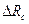 , можно выявить только в частном случае
, можно выявить только в частном случае 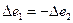 .
.
Дата добавления: 2016-06-18; просмотров: 4552;











