Коэффициент Дарси при турбулентном движении жидкости, экспериментальные методы его определения
Для определения значений коэффициентов сопротивлений опытным путём может быть использована, например, установка, изображённая на рис. 1.22 установка состоит из центробежного насоса А, нагнетательной линии В, напорного резервуара С, снабжённого сливной линией D, опытного участка трубопровода Е, приёмного резервуара F и всасывающей линии G.
Во время производства опытов жидкость насосом подаётся в напорный резервуар (в котором благодаря наличию сливной линии поддерживается постоянный уровень) и оттуда поступает в трубопровод.
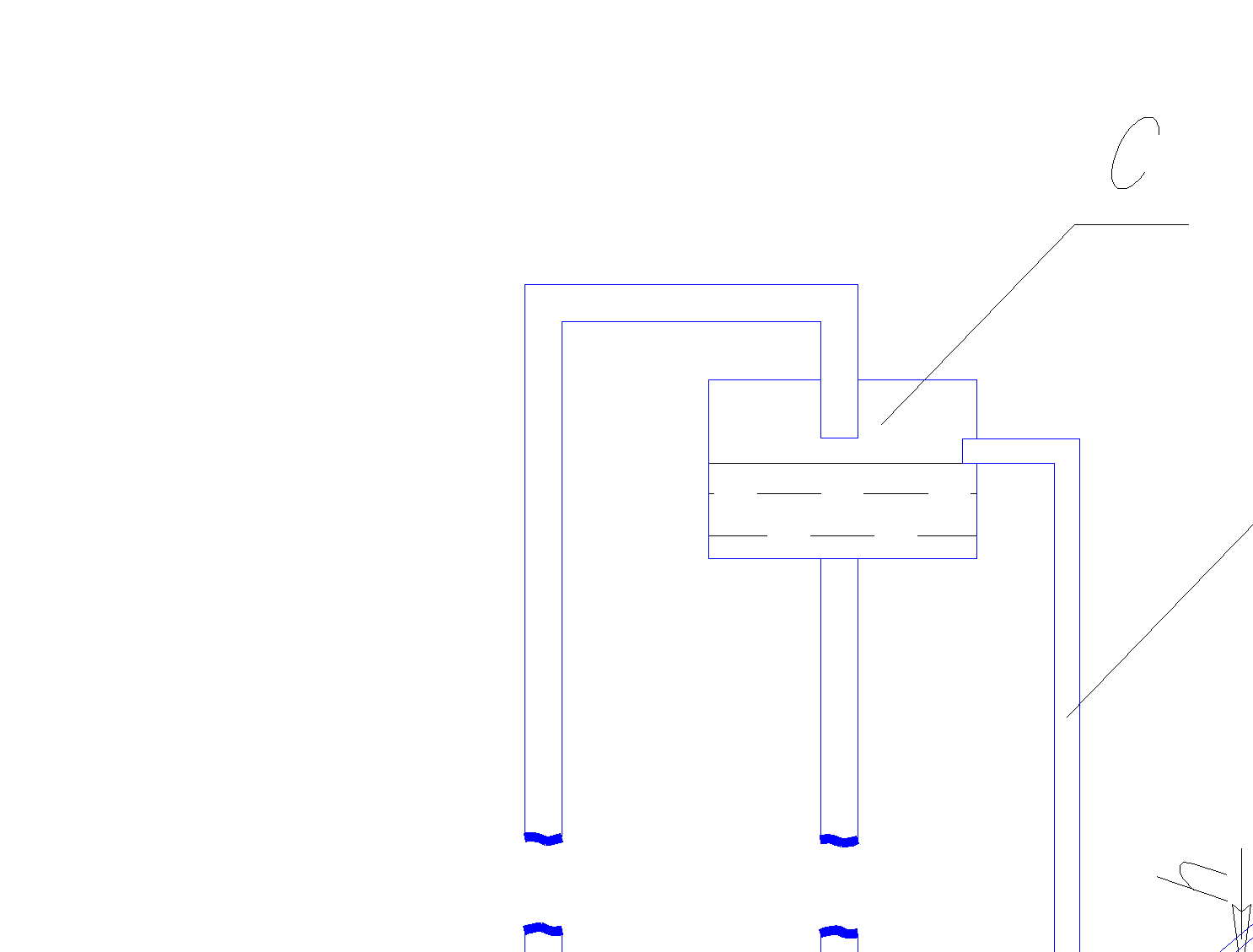 рис. 1.22 Установка для определения коэффициентов сопротивления
рис. 1.22 Установка для определения коэффициентов сопротивления
|
Из трубопровода Е жидкость вытекает в приёмный резервуар и из него по всасывающей линии забирается насосом. Таким образом, во всё время опыта имеет место непрерывная циркуляция жидкости в системе.
Измерение расхода жидкости Q осуществляется при помощи водометра Вентури H (в других случаях расход может быть замерен объёмным или весовым способом, для чего между трубопроводом и приёмным резервуаром вводится мерный бак).
Линейные потери напора определяются по показанию дифференциального ртутного манометра K. Для большей надёжности измерений целесообразно установить два манометра, взаимно контролирующих друг друга. При этом следует иметь ввиду, что длина опытного участка трубопровода должна быть взята достаточно большой, так как при малой длине разность уровней в коленах ртутного манометра может оказаться незначительной и практически неощутимой; в подобных случаях вместо ртутного манометра необходимо применять дифференциальный пьезометр.
При горизонтальном трубопроводе постоянного диаметра линейные потери напора по длине L между сечениями трубопровода a и b, к которым присоединён дифференциальный манометр, определяются выражением
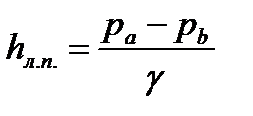 (1.77)
(1.77)
вспоминая, что 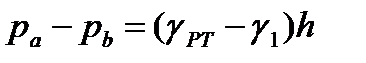 (1.78)
(1.78)
(где 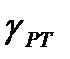 - удельный вес ртути,
- удельный вес ртути, 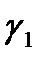 - удельный вес движущейся по трубопроводу жидкости,
- удельный вес движущейся по трубопроводу жидкости, 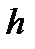 - разность уровней ртути в манометре), получаем:
- разность уровней ртути в манометре), получаем:
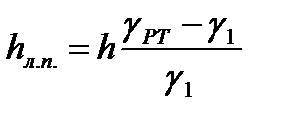 (1.79)
(1.79)
Из формулы Дарси-Вейсбаха имеем, далее,
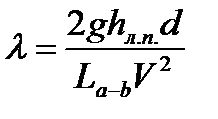 , (1.80)
, (1.80)
где потеря напора 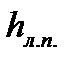 известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q:
известна, а средняя скорость V может быть вычислена по измеренному расходу жидкости Q:
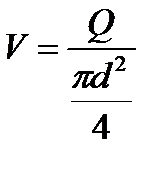 (1.81)
(1.81)
Измерения расхода и напора производятся несколько раз при различных скоростях движения жидкости по трубопроводу. После этого вычисляются соответствующие значения коэффициента 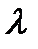 и числа Рейнольдса и строится кривая изменения коэффициента
и числа Рейнольдса и строится кривая изменения коэффициента 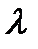 в зависимости от Re.
в зависимости от Re.
Для определения коэффициентов местного сопротивления в трубопроводе устанавливается на фланцах исследуемое сопротивление (расширяющийся или сужающийся патрубок, диафрагма и т.п.) и аналогично предыдущему находится полная потеря напора между сечениями a и b. Предварительно следует найти потерю напора в этом же трубопроводе, при той же самой скорости движения жидкости, но без местного сопротивления.
Местная потеря напора 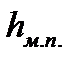 определяется как разность потерь напора в обоих случаях, после чего по формуле
определяется как разность потерь напора в обоих случаях, после чего по формуле
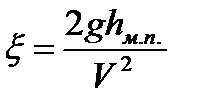 (1.82)
(1.82)
вычисляется значение коэффициента местного сопротивления.
График Никурадзе
Если для гидравлически гладких труб коэффициент потерь на трение вполне определяется числом Рейнольдса, то для шероховатых труб 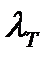 зависит ещё и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер
зависит ещё и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер  бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость
бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т.е. так называемая относительная шероховатость 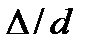 . Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер
. Одна и та же абсолютная шероховатость может совершенно не оказывать влияния на сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер  и одинаковую форму, т.е. при так называемой равномерно распределённой зернистой шероховатости.
и одинаковую форму, т.е. при так называемой равномерно распределённой зернистой шероховатости.
Таким образом, в этом случае коэффициент 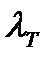 зависит как от Рейнольдса, так и от отношения
зависит как от Рейнольдса, так и от отношения 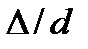 (или
(или 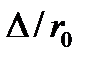 ):
):
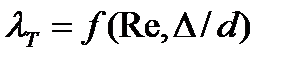 (1.83)
(1.83)
Характер влияния этих двух параметров на сопротивление труб отчётливо виден из графика, который является результатом опытов И.И. Никурадзе.
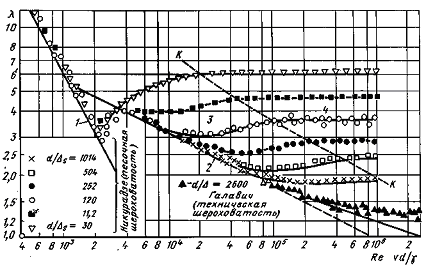 Рис 1.23. Экспериментальная зависимость гидравлического коэффициента трения А, от числа Рейнольдса
Рис 1.23. Экспериментальная зависимость гидравлического коэффициента трения А, от числа Рейнольдса 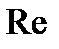 и относительной гладкости при песочной шероховатости (график Никурадзе) и относительной гладкости при песочной шероховатости (график Никурадзе)
|
И.И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путём приклейки песчинок определённого размера,. Полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределённая зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей ( 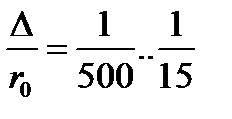 ), а также чисел
), а также чисел
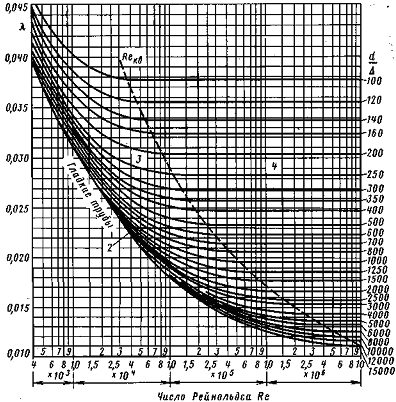 Рис. 2.24. Экспериментальные зависимости гидравлического коэффициента трения
Рис. 2.24. Экспериментальные зависимости гидравлического коэффициента трения  от числа Рейнольдса от числа Рейнольдса 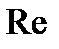 и относительной гладкости стенок для промышленных труб с неравномерной шероховатостью и относительной гладкости стенок для промышленных труб с неравномерной шероховатостью
|
Re ( 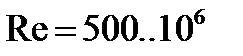 ). Результаты этих испытаний представлены в виде кривых зависимости
). Результаты этих испытаний представлены в виде кривых зависимости 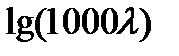 от
от 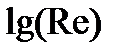 для ряда значений
для ряда значений 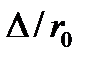 .
.
Из графика можно сделать следующие выводы:
1. При ламинарном течении шероховатость на сопротивление не влияет.
2. Критическое число Рейнольдса от шероховатости практически не зависит;
3. В области турбулентного течения, но при небольших Re и 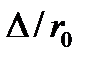 шероховатость на сопротивление не влияет;
шероховатость на сопротивление не влияет;
4. При больших Re и больших относительных шероховатостях коэффициент 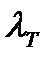 перестаёт зависеть от Re и становится постоянным для данной относительной шероховатости.
перестаёт зависеть от Re и становится постоянным для данной относительной шероховатости.
Дата добавления: 2016-05-28; просмотров: 4179;











