Принцип импульсного регулирования напряжения.
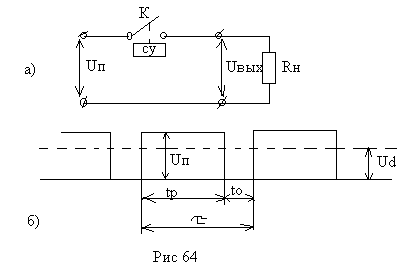
В основе работы импульсных преобразователей лежит следующий принцип. Предположим, что нагрузка подключена к источнику напряжения через ключевой элемент “к”, который периодически замыкается и размыкается.
Время замкнутого (tр) и разомкнутого (t0) состояний ключа можно автоматически изменять, воздействуя на него сигналами, поступающими из системы управления “СУ”. В результате к нагрузке будет приложено импульсное напряжение, форма которого соответствует диаграмме, представленной на рис 64б.
Очевидно, что среднее значение напряжения на нагрузке будет зависеть от соотношения времени замкнутого и разомкнутого состояний ключа К.
Согласно определению среднего значения напряжения можно записать:
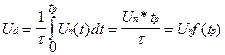 (4-67)
(4-67)
где Ud - среднее значение напряжения на нагрузке;
t = tр + t0 - период переключения ключа или время цикла регулирования;
¦ = 1/t - частота переключения ключа.
Отношение (tр /t) = g (4-68) называют коэффициентом заполнения периода рабочим импульсом. Изменяя g, можно регулировать выходное напряжение на нагрузке.
Иногда рассматривается обратная величина q = (1/ g) = (t / tр), которая называется скважностью работы ключа.
При установлении соотношений между входным и выходным напряжениями, выявляя зависимость тока импульсного преобразователя от регулирующей переменной мы будем использовать коэффициент g.
Регулирование напряжения в рассматриваемой схеме за счет изменения коэффициента g можно рассматривать как широтно-импульсное регулирование напряжения на нагрузке.
Возможны три способа регулирования напряжения:
Широтно-импульсное регулирование (ШИР), когда время tр - переменное, а частота ¦- постоянная;
Частотно- импульсное регулирование (ЧИР), когда время tр - постоянное, а частота ¦- переменная;
Широтно-частотное регулирование, когда время tр и частота ¦ - переменные.
Чаще всего используется первый способ регулирования выходного напряжения. Его мы будем рассматривать.
Таким образом время рабочего импульса и время паузы связаны с g соотношениями:
tр = gt (4-69)
t0= (1- g)t (4-70)
Схема регулирования напряжения и диаграмма, изображенные на рис 64, могут быть реализованы лишь при активном сопротивлении нагрузки.
При использовании импульсного регулирования в системах электропривода нагрузка имеет активно- индуктивный характер и часто в составе нагрузки присутствует источник ЭДС.
В таком случае должен быть предусмотрен обратный вентиль. Он обеспечивает непрерывность тока в нагрузке при разрыве цепи импульсным элементом (ключом). На рис 65 изображена схема диаграммы напряжения и тока при активно- индуктивной нагрузке с противо-ЭДС.
На основании баланса энергии, поступающей в нагрузку из сети (от Uпит) и энергии, которая тратится в нагрузке, выявим зависимость, (связь) между средним значением тока, напряжением питания Uпит , ЭДС нагрузки Eн и коэффициентом g. При получении этой зависимости введем допущение, что среднее и действующее значение тока в нагрузке равны. Это может иметь место при идеальной сглаженности тока (если Lн = ¥).
Uн I tр = Eн I tр + I2 Rн tр + WL (1)
WL = Eн I t0 + I2 Rн t0
Uн I tр = Eн I t + I2 Rн t (2)
Uн tр = Eн t + I Rн t
Разделим левую и правую части на t, тогда:
Uн g = Eн + I Rн
g = (Eн + I Rн )/ Uн (4-71)
I = (Uн g - Eн )/ Rн (4-72)
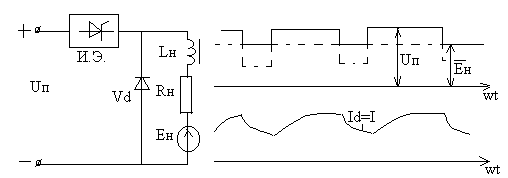
Рис 65
Уравнение (1) представляет собой уравнение баланса поступающей в нагрузку из сети энергии за время одного рабочего импульса (tр) и энергии, тратящейся в нагрузке за время t. WL - энергия, накапливаемая в индуктивности за время tр. Этой энергии достаточно для поддержания тока в нагрузке, равного I за время паузы (t0).
Прибавив к правой части уравнения значение WL , получаем уравнение баланса энергии (2). Дальнейшие действия ясны без пояснений.
Уравнение (4-71) дает связь переменной g с переменными I ,Uн ,Eн .
Уравнение (4-72) показывает, что регулирование тока в цепи нагрузки можно осуществлять изменением g при неизменных Rн ,Uн ,Eн.
Дата добавления: 2016-06-18; просмотров: 3636;











