Основной закон и уравнение теплопроводности

Опытным путем установлено, что плотность теплового потока, передаваемого теплопроводностью, прямо пропорциональна градиенту температуры:

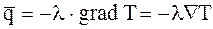(1)

где l - коэффициент теплопроводности, определяемый опытным путем и зависящий от агрегатного состояния вещества, температуры, давления, структуры, плотности, пористости и влажности. Знак минус указывает на то, что векторы q и grad T имеют противоположное направление.

Уравнение (1) является математическим выражением закона теплопроводности ФУРЬЕ, а значение l характеризует интенсивность процесса теплопроводности и числено равно плотности теплового потока при градиенте температуры, равном единице. Количество теплоты Q_t, теряемое произвольным объемом V внутри тела, можно определить путем интегрирования плотности теплового потока q по замкнутой поверхности S, ограничивающей этот объем так, что

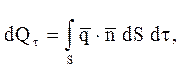
где - единичный вектор, направленный по нормали к поверхности; t - время.

Используя формулу Остроградского-Гаусса, получим:

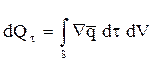. (2)

В соответствии с первым законом термодинамики это количество теплоты может появиться лишь за счет уменьшения внутренней энергии единицы объема тела в единицу времени

, а также за счет действия внутренних источников теплоты мощностью q_V (Вт/м³), которые могут иметь различную физическую природу. Поэтому

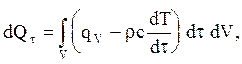(3)

где с - удельная теплоемкость тела.

Левые части выражений (2) и (3) равны, поэтому

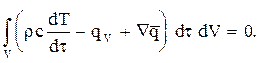
Так как объем V выбран произвольно, равенство нулю интеграла означает, что

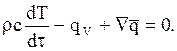(4)

Перенос теплоты в твердом теле осуществляется путем теплопроводности, поэтому с учетом уравнения (1) и соотношения 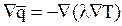уравнение теплопроводности примет вид:

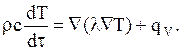(5)

Уравнение (5) можно записать в виде

(6)

где а - коэффициент температуропроводности, характеризующий скорость выравнивания температуры неравномерно нагретого тела (м²/с). При отсутствии внутренних источников теплоты и с учетом уравнения (*) можно получить

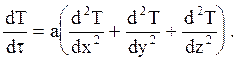(6a)

Уравнения (6, 6а) выражают зависимость изменения во времени температуры в некоторой точке тела от свойств тела и производительности источников теплоты в окрестности этой точки, т.е. устанавливают связь между пространственными и временными изменениями температуры. Для получения однозначного решения уравнений (6, 6а) необходимо выполнение следующих условий, которые называют условиями однозначности.