Замечательные пределы
|
Рассмотрим функцию
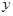 =
= 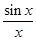 . Она не определена в точке
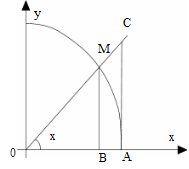
. Она не определена в точке  = 0, тем не менее предел её в этой точке существует и равен единице. Докажем это. Из чертежа при
= 0, тем не менее предел её в этой точке существует и равен единице. Докажем это. Из чертежа при
0 <  <
< 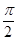 ясно, что
ясно, что
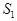 <
< 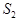 <
< 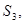 (1)
(1)
где 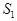 и
и 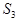 – площади треугольников ОМВ и ОСА, а
– площади треугольников ОМВ и ОСА, а 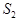 – площадь кругового сектора. Радиус окружности будем считать равным единице. Тогда, выражая площади через угол
– площадь кругового сектора. Радиус окружности будем считать равным единице. Тогда, выражая площади через угол  , неравенство (1) перепишем так:
, неравенство (1) перепишем так: 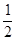
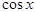 ×
× 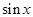 <
< 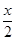 <
< 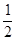
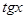 , или
, или
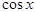 <
< 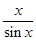 <
< 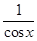 Þ
Þ 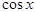 <
< 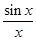 <
< 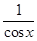 . (2)
. (2)
В неравенстве (2) все функции являются четными, поэтому оно верно и для отрицательных  , т.е. при
, т.е. при 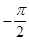 <
<  <
< 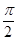 ,
,  ¹ 0. Устремляя
¹ 0. Устремляя  к нулю и пользуясь теоремой о двух милиционерах, получим
к нулю и пользуясь теоремой о двух милиционерах, получим
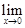
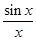 = 1. (3)
= 1. (3)
Формулу (3) называют первым замечательным пределом.
Прежде, чем перейти ко второму замечательному пределу, приведем формулу бинома Ньютона
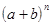 =
= 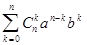 , (4)
, (4)
где 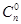 = 1,
= 1, 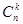 =
= 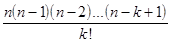 ,
, 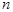 Î N,
Î N,
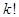 = 1×2×3×...×
= 1×2×3×...× 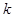 .
.
Формулу (4) можно доказать методом математической индукции. Мы её докажем позже другим методом.
Рассмотрим последовательность 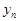 =
= 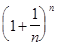 . Используя формулу бинома Ньютона, получим
. Используя формулу бинома Ньютона, получим
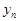 = 1 +
= 1 + 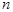 ×
× 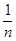 +
+ 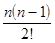
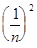 +
+ 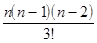
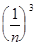 + ... +
+ ... +
+ 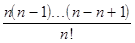
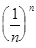 = 1 + 1 +
= 1 + 1 + 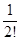
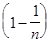 +
+
+ 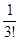
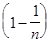
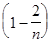 +...+
+...+ 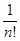
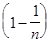
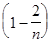 ...
... 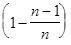 . (5)
. (5)
Из (5) видно, что последовательность { 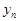 } монотонно возрастающая, т.к. при замене n на n + 1 каждое слагаемое в (5) возрастает и добавляется еще одно положительное слагаемое.
} монотонно возрастающая, т.к. при замене n на n + 1 каждое слагаемое в (5) возрастает и добавляется еще одно положительное слагаемое.
Покажем теперь, что эта последовательность ограниченна сверху. Действительно,
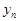 < 1 + 1 +
< 1 + 1 + 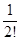 +
+ 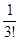 + ... +
+ ... + 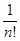 £ 1 + 1 +
£ 1 + 1 + 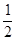 +
+ 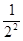 +...+
+...+ 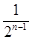 =
=
= 1 + 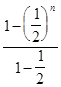 = 1 + 2 –
= 1 + 2 – 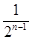 £ 3, " n Î N. (6)
£ 3, " n Î N. (6)
(Сначала мы отбросили скобки меньшие единицы, и результат возрос. Затем учли, что 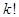 ³
³ 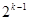 и воспользовались формулой суммы членов убывающей геометрической прогрессии со знаменателем q =
и воспользовались формулой суммы членов убывающей геометрической прогрессии со знаменателем q = 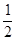 ).
).
Итак, последовательность { 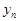 } монотонно возрастает и ограниченна сверху, следовательно, имеет предел (см. Теорему 2 §2). Этот предел называют числом е.
} монотонно возрастает и ограниченна сверху, следовательно, имеет предел (см. Теорему 2 §2). Этот предел называют числом е.
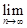
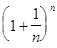 = е. (7)
= е. (7)
Число е является иррациональным, е = 2,718... .
Рассмотрим теперь функцию 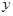 =
= 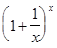 и докажем, что она имеет предел при
и докажем, что она имеет предел при 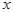 ® + ¥ равный е. Для любого положительного действительного числа
® + ¥ равный е. Для любого положительного действительного числа 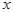 имеет место неравенство n £
имеет место неравенство n £ 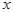 < n + 1. Для обратных величин этого неравенства получим
< n + 1. Для обратных величин этого неравенства получим
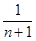 <
< 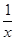 £
£ 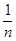 Þ 1 +
Þ 1 + 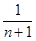 < 1 +
< 1 + 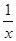 £ 1 +
£ 1 + 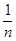 .
.
Если левую часть последнего неравенства возвести в степень n, среднюю – в степень x, а правую – в степень n + 1 , то неравенство только усилится, т.е.
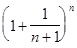 <
< 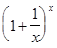 £
£ 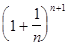 . (8)
. (8)
Легко убедиться, что 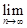
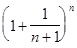 = e,
= e, 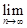
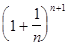 = e.
= e.
Поэтому из (8) по теореме о двух милиционерах следует, что
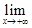
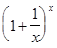 = e. (9)
= e. (9)
Покажем теперь, что 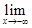
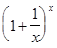 = e. Действительно,
= e. Действительно,
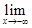
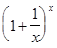 =
= 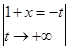 =
= 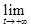
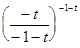 =
=
= 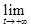
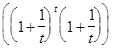 = e.
= e.
Последняя формула и формула (9) называются вторым замечательным пределом.
Можно доказать, что
1) 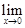
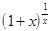 = e, 4)
= e, 4) 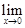
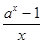 =
= 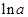 ,
,
2) 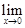
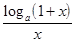 =
= 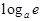 , 5)
, 5) 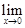
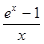 = 1,
= 1,
3) 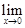
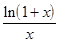 = 1, 6)
= 1, 6) 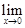
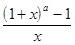 =
=  .
.
Дата добавления: 2020-02-05; просмотров: 333;











