Предел последовательности
Рассмотрим последовательность 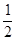 ,
, 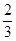 ,
, 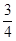 , ... . Её можно рассматривать как переменную величину
, ... . Её можно рассматривать как переменную величину  =
= 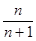 ,
,
n = 1,2,3, ... , функцию натурального аргумента  =
= 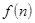 . Значение данной переменной величины
. Значение данной переменной величины  отличается от единицы на 0,1 при n = 9, на 0,01 при n = 99, на 0,001 при
отличается от единицы на 0,1 при n = 9, на 0,01 при n = 99, на 0,001 при
n = 999 и т.д. Очевидно, что эта переменная величина может как угодно близко приблизиться к единице. Говорят, что единица является её пределом.
Определение 1. Число  называется пределом числовой последовательности
называется пределом числовой последовательности 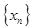 , если для любого сколь угодно малого числа
, если для любого сколь угодно малого числа  > 0 существует такой номер
> 0 существует такой номер 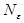 , что все значения
, что все значения  при n >
при n > 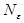 удовлетворяют неравенству
удовлетворяют неравенству 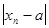 <
<  .
.
Пишут 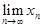 =
=  .
.
Геометрически это означает, что для любой O (  ,
,  ) найдётся такой номер
) найдётся такой номер 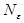 , что все
, что все  при n >
при n > 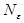 будут принадлежать этой
будут принадлежать этой  –окрестности. ("
–окрестности. ("  > 0 $
> 0 $ 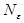 (n >
(n > 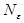 Þ
Þ  Î O (
Î O (  ,
,  ))).
))).
Если  = C = const, то
= C = const, то 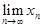 = C, т.к.
= C, т.к. 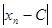 = 0 <
= 0 <  для любых n.
для любых n.
Чтобы найти предел последовательности, используя только его определение, следует поступить так:
1) предположить, что предел равен  ;
;
2) решить неравенство 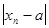 <
<  относительно n для любого
относительно n для любого  > 0;
> 0;
3) если решение неравенства имеет вид n > 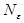 , то предположение, что предел равен
, то предположение, что предел равен  , верно и предел найден.
, верно и предел найден.
Пример1. Найти предел последовательности  =
= 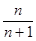 .
.
Решение. 1) Предположим, что  = 1.
= 1.
2) Решим неравенство 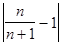 <
<  ,
,
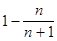 <
<  ,
, 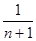 <
<  ,
,
n + 1 > 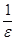 , n >
, n > 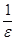 – 1 =
– 1 = 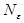 .
.
3) Итак, для всех n > 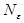 неравенство
неравенство
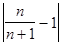 <
<  выполняется, поэтому
выполняется, поэтому 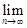
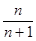 =1 согласно определению предела.
=1 согласно определению предела.
Замечание. Число 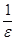 – 1 не для всех
– 1 не для всех  является натуральным, поэтому за
является натуральным, поэтому за 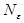 следует взять целую часть этого числа, т.е.
следует взять целую часть этого числа, т.е. 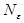 = Е (
= Е ( 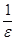 – 1).
– 1).
Теорема 1. Если последовательность имеет предел, то он единственный.
Доказательство (от противного). Пусть предел не единственный. Выберем два предела  =
= 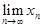 и
и  = =
= = 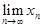 ,
,
 <
<  . Выберем O (
. Выберем O (  ,
,  ) и O (
) и O (  ,
,  ) так, чтобы они не имели общих точек. Для этого достаточно взять
) так, чтобы они не имели общих точек. Для этого достаточно взять  <
< 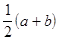 . По определению предела $
. По определению предела $ 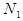 " n >
" n > 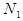 (
(  Î O (
Î O (  ,
,  )) и $
)) и $ 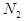 " n >
" n > 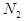 (
(  Î O(
Î O(  ,
,  )). Пусть
)). Пусть 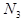 = max (
= max ( 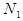 ,
, 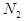 ), тогда " n >
), тогда " n > 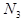 (
(  ÎO (
ÎO (  ,
,  ) ^
) ^  Î O(
Î O(  ,
,  )), что не возможно, т.к. окрестности не пересекаются. ( ^ - символ конъюнкции). Полученное противоречие доказывает теорему.
)), что не возможно, т.к. окрестности не пересекаются. ( ^ - символ конъюнкции). Полученное противоречие доказывает теорему.
Определение 2. Последовательность 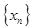 называется бесконечно большой (пишут
называется бесконечно большой (пишут 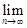
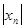 = ¥), если для любого значения М > 0 найдётся такой номер
= ¥), если для любого значения М > 0 найдётся такой номер 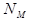 , что все значения
, что все значения  при n >
при n > 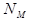 удовлетворяют неравенству
удовлетворяют неравенству 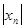 > M.
> M.
Например, последовательности  = n,
= n, 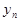 = – n,
= – n, 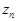 =
=
= 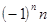 являются бесконечно большими.
являются бесконечно большими.
Замечание. Следует различать неограниченную и бесконечно большую последовательности. Например, последовательность 1, 0,3,0,5,0, ... является неограниченной сверху, но она не является бесконечно большой.
Если последовательность имеет конечный предел, то она называется сходящейся. В противном случае – расходящейся. Последовательность 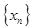 называется неубывающей, если
называется неубывающей, если  £
£ 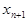 для любого n. Если
для любого n. Если  ³
³ 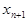 , – то это невозрастающая последовательность. Невозрастающая и неубывающая последовательности называются монотонными. Если неравенства строгие (
, – то это невозрастающая последовательность. Невозрастающая и неубывающая последовательности называются монотонными. Если неравенства строгие (  <
< 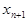 ,
,  >
> 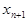 ) , то последовательности называются строго монотонными.
) , то последовательности называются строго монотонными.
Теорема 2. Монотонная ограниченная последовательность сходится.
Доказательство. Пусть последовательность неубывающая, т.е.  £
£ 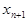 . Согласно теореме 3 §1 последовательность
. Согласно теореме 3 §1 последовательность 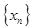 имеет точную верхнюю грань sup
имеет точную верхнюю грань sup  = M. По определению точной верхней грани
= M. По определению точной верхней грани  £ M для любого n и M –
£ M для любого n и M – 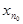 <
<  , где
, где 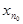 – некоторый член последовательности. Поскольку последовательность неубывающая, то последнее неравенство будет выполняться для всех n ³ n0, т.е.
– некоторый член последовательности. Поскольку последовательность неубывающая, то последнее неравенство будет выполняться для всех n ³ n0, т.е. 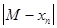 <
<  " n > n0. А это означает, что M =
" n > n0. А это означает, что M = 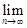
 . Доказательство аналогично для невозрастающей последовательности. Теорема доказана.
. Доказательство аналогично для невозрастающей последовательности. Теорема доказана.
Предел функции
Пусть функция 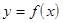 определена в окрестности точки
определена в окрестности точки  =
=  за исключением, быть может, самой точки
за исключением, быть может, самой точки  . Точка
. Точка  может быть и бесконечно удалённой.
может быть и бесконечно удалённой.
Определение 1 (Гейне). Число  называется пределом функции
называется пределом функции 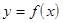 в точке
в точке  =
=  , если для любой сходящейся к
, если для любой сходящейся к  последовательности аргумента
последовательности аргумента 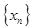 соответствующая последовательность значений функции
соответствующая последовательность значений функции 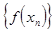 сходится к
сходится к  .
.
Пишут 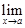
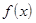 =
=  , или
, или 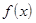 ®
®  при
при 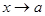 .
.
Если предел функции существует, то он единственный. Это следует из единственности предела последовательности.
Пример 1. Найти 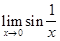 .
.
Решение. Пусть предел существует. Выберем две последовательности аргумента, сходящиеся к нулю:
 =
= 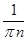 и
и 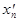 =
= 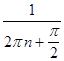 . Соответствующие последовательности значений функции следующие:
. Соответствующие последовательности значений функции следующие:
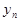 =
= 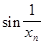 =
=
= 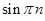 = 0,
= 0, 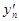 =
= 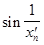 =
= 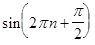 = 1,
= 1,
т.е. обе последовательности являются постоянными. Поскольку пределом постоянной является сама постоянная (см. §2), то в точке  = 0 мы получим два предела функции 0 и 1, чего не может быть. Следовательно наше предположение о существовании предела в точке
= 0 мы получим два предела функции 0 и 1, чего не может быть. Следовательно наше предположение о существовании предела в точке  = 0 не верно. Данная функция не имеет предела в нуле.
= 0 не верно. Данная функция не имеет предела в нуле.
Определение 2 (Коши). Число  называется пределом функции
называется пределом функции 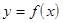 в точке
в точке  =
=  , если для любого
, если для любого  > 0 существует число
> 0 существует число 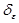 > 0 такое, что для всех
> 0 такое, что для всех  Î O(
Î O(  ,
, 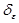 ) имеет место неравенство
) имеет место неравенство 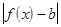 <
<  . ("
. ("  > 0 $ O (
> 0 $ O (  ,
, 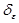 )
)  Î O(
Î O(  ,
, 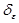 ) Þ
) Þ 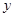 Î O (
Î O (  ,
,  )).
)).
Пример 2. Доказать, что 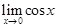 = 1.
= 1.
Решение. По определению Коши 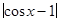 <
<  , если
, если 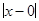 =
= 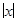 <
< 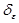 . Если найдем
. Если найдем 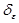 для любого
для любого  > 0 такое, что из второго неравенства будет следовать первое, то задача будет решена.
> 0 такое, что из второго неравенства будет следовать первое, то задача будет решена.
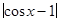 = 1 –
= 1 – 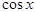 =
= 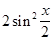 £ 2 ×
£ 2 × 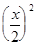 <
<  Þ
Þ 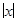 <
< 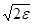 .
.
Положим 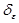 =
= 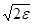 , тогда для всех
, тогда для всех 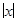 <
< 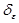 выполняется неравенство
выполняется неравенство 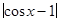 <
<  и задача решена.
и задача решена.
Упражнение. Доказать, что 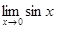 = 0.
= 0.
Замечание. Выше приведено два определения предела функции, однако определение должно быть единственным. Поэтому, если за определение взять формулировку Гейне, то формулировка Коши будет теоремой, и её можно доказать. И наоборот.
|
Определение 3. Функция 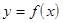 называется бесконечно большой в точке
называется бесконечно большой в точке  =
=  , если существует такая
, если существует такая 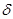 -окрестность этой точки, что для "
-окрестность этой точки, что для "  Î O (
Î O (  ,
, 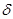 )
) 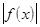 > M , где М > 0 – любое действительное число. Точка
> M , где М > 0 – любое действительное число. Точка  может быть и бесконечно удалённой. ($ M > 0 $
может быть и бесконечно удалённой. ($ M > 0 $ 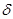 > 0 (
> 0 (  Î O (
Î O (  ,
, 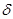 ) Þ
) Þ 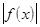 > M).
> M).
Если  ®
®  , оставаясь меньше
, оставаясь меньше  , то предел функции
, то предел функции 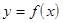 в точке называется левым. Пишут
в точке называется левым. Пишут  =
= 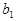 . Если
. Если  ®
®  , оставаясь больше
, оставаясь больше  , то предел называют правым. Пишут
, то предел называют правым. Пишут 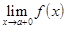 =
= 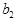 . Правый и левый пределы называют односторонними пределами. Если
. Правый и левый пределы называют односторонними пределами. Если 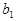 ¹
¹ 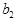 , то функция в точке
, то функция в точке  =
=  предела не имеет, а имеет только односторонние пределы. Если
предела не имеет, а имеет только односторонние пределы. Если 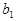 =
= 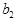 , то функция имеет в точке
, то функция имеет в точке  предел. И наоборот, если функция имеет предел в точке
предел. И наоборот, если функция имеет предел в точке  =
=  , то она имеет равные между собой левый и правый пределы.
, то она имеет равные между собой левый и правый пределы.
Дата добавления: 2020-02-05; просмотров: 229;










