Многократные прямые измерения
Основная задача обработки многократных измерений, заключается в нахождении результата измерения ФВ и доверительного интервала, в котором находится ее истинное (действительное) значение.
Исходной информацией для обработки является ряд из n (n > 4) результатов единичных измерений x1, x2, ..., xn, из которых исключены известные систематические погрешности. Число измерений зависит от требований к точности получаемого результата и от реальной возможности выполнения повторных измерений.
Последовательность обработки результатов многократных измерений включает в себя ряд этапов:
1) исключение из результатов измерений известных систематических погрешностей;
2) вычисление среднего арифметического значения 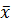 измеряемой величины из n единичных результатов;
измеряемой величины из n единичных результатов;
3) вычисление средней квадратической погрешности единичных измерений в ряду измерений σx;
4) исключение промахов (грубых погрешностей измерений);
5) вычисление средней квадратической погрешности результата измерений среднего арифметического 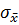 ;
;
6) проверку гипотезы о принадлежности результатов измерений нормальному закону;
7) вычисление доверительных границ случайной погрешности измерений ±ε;
8) вычисление доверительных границ неисключенной систематической погрешности результата измерений ±θ;
9) вычисление доверительных границ погрешности результата измерений ±∆;
10) представление результата измерения в виде 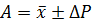 , где P - доверительная вероятность.
, где P - доверительная вероятность.
Известные систематические погрешности исключают введением в результат измерений соответствующих поправок, численно равных систематическим погрешностям, но противоположным им по знаку. Поправку вводят в результаты единичных измерений, а если известно, что результаты всех единичных измерений имеют одинаковые систематические погрешности, ее исключают из среднего арифметического значения измеряемой величины.
Среднее арифметическое значение измеряемой величины из n
единичных результатов 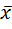 рассчитывают по формуле
рассчитывают по формуле
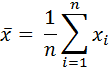
Для определения средней квадратической погрешности (СКП) единичных измерений в ряду измерений 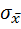 используют формулу
используют формулу
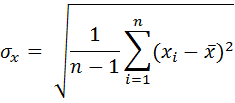
Промахи (грубые погрешности) могут сильно исказить результат измерений, поэтому их исключение из ряда измерений обязательно.
Среднюю квадратическую погрешность результата измерений (СКПр)
среднего арифметического значения σx вычисляют по формуле
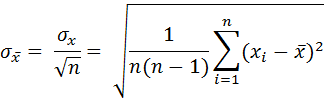
Гипотезу о принадлежности результатов измерений нормальному закону проверяют с помощью специальных критериев, если число измерений n > 50; составной критерий используют, если 15 < n < 50. При n ≤15 гипотезу о нормальном законе распределения результатов измерений не проверяют, предполагая, что вид закона распределения известен заранее. Это, как правило, нормальный закон распределения.
При заданном значении доверительной вероятности Р и числе единичных измерений n по таблицам функций определяют значения параметров.
Рассмотрим определение доверительного интервала результата измерений при отсутствии систематической погрешности.
Вероятность того, что истинное значение x измеряемой величины находится в пределах от xн до xв
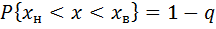
где q - уровень значимости.
Здесь Р называют доверительной вероятностью, а интервал от хн до хв - доверительным интервалом результата измерений.
Будем полагать, что значение случайной величины х подчиняется нормальному закону распределения, то доверительный интервал симметричен относительно точечной оценки 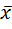 и определяется из таблиц значений интегральной функции Лапласа
и определяется из таблиц значений интегральной функции Лапласа 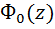 :
:
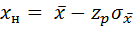
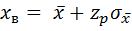
где 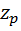 - аргумент функции Лапласа
- аргумент функции Лапласа 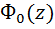 , отвечающий вероятности Р/2.
, отвечающий вероятности Р/2.
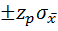 - доверительные границы погрешности результата измерений.
- доверительные границы погрешности результата измерений.
Полученный доверительный интервал определяется по формуле
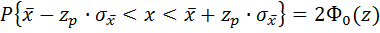
Вычисление доверительных границ производится, как правило, с доверительной вероятностью Р = 0,90; 0,95 или 0,99.
Пример. Выполнено 45 единичных измерений линейного размера детали с помощью индикатора часового типа, установленного на стойке. Получены следующие исправленные результаты измерений:
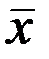 = 19,95 мм,
= 19,95 мм, 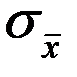 = 0,13 мм. Определить доверительный интервал результата измерений, если закон распределения - нормальный, а доверительная вероятность Р = 0,95.
= 0,13 мм. Определить доверительный интервал результата измерений, если закон распределения - нормальный, а доверительная вероятность Р = 0,95.
1. По формуле найдем СКП результата измерений среднего арифметического, мм:
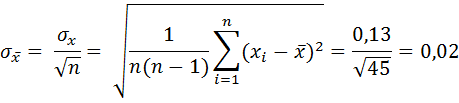
2. По таблице, значений функции Лапласа
Значение интеграла
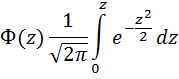
определим для Р/2 = 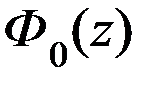 = 0,475 аргумент функции Лапласа
= 0,475 аргумент функции Лапласа 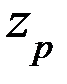 = 1,96.
= 1,96.
Следовательно, доверительный интервал результата измерений, в мм:
(19,95 - 0,02 ∙ 1,96) < х < (19,95 + 0,02 ∙ 1,96)
или 19,91 < х < 19,99.
При нахождении случайной погрешности с использованием функции Лапласа доверительная вероятность по формуле
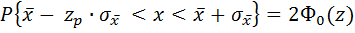
характеризует вероятность того, что отдельные единичные измерения хi не будут отклоняться от истинного значения более чем 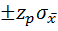 при большом числе измерений.
при большом числе измерений.
Однако при определении доверительного интервала при многократных измерениях важнее знать отклонение от истинного значения среднего арифметического значения ряда измерений. Из математической статистики известно, что если результат единичных измерений при небольшом числе измерений подчиняется нормальному закону, то распределение средних арифметических значений ряда измерений подчиняется закону Стьюдента с тем же средним арифметическим значением 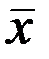 .
.
Особенностью распределения Стьюдента является то, что доверительный интервал с уменьшением числа измерений расширяется по сравнению с нормальным законом распределения при той же доверительной вероятности. В связи с этим при ограниченном числе измерений, определяя доверительный интервал, рекомендуется использовать распределение Стьюдента.
Пример. При многократном измерении диаметра вала Ø30 h9(-0,0052) микрометром МК25-1 получены следующие результаты:
| Измерение микрометром размера вала мм | |||||||
| № | |||||||
| И | 29,94 | 29,95 | 29,96 | 29,97 | 29,97 | 29,98 | 29,98 |
Не учтенная систематическая погрешность, вызванная отклонением температуры вала от нормальной, θ = 2 мкм.
Определить, является ли результат х1 = 29,94 мм промахом, найти и записать в стандартной форме результат измерений (доверительная вероятность P=0,95).
1. Определим среднее арифметическое значение измеряемой величины, мм:
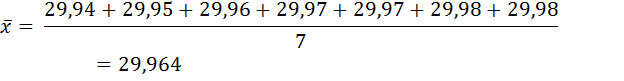
2. Рассчитаем СКП единичных измерений, мм:
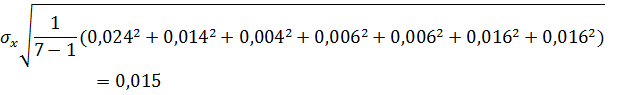
3. Так как число измерений n < 10, а закон распределения результатов единичных измерений неизвестен, промах вычислим с использованием критерия Романовского:
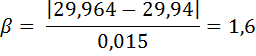
Для ближайшего меньшего n = 6 и q = 0,05 (при Р = 0,95) по таблице Романовского найдем 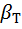 = 2,10, т.е.
= 2,10, т.е. 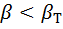 и результат х1 = 29,94 промахом не является.
и результат х1 = 29,94 промахом не является.
Значения 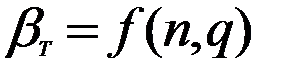
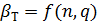
| Уровень значимости q | Число измерений | ||||||
| n=4 | n=6 | n=8 | n=10 | n=12 | n=14 | n=16 | |
| 0,01 | 1,73 | 2,16 | 2,43 | 2,62 | 2,75 | 2,90 | 3,08 |
| 0,02 | 1,72 | 2,13 | 2,37 | 2,54 | 2,66 | 2,80 | 2,96 |
| 0,05 | 1,71 | 2,10 | 2,27 | 2,41 | 2,52 | 2,69 | 2,78 |
| 0,10 | 1,69 | 2,00 | 2,17 | 2,29 | 2,39 | 2,49 | 2,62 |
4. Определим СКП результата измерений среднего арифметического значения, мм:
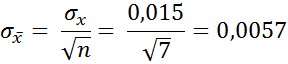
5. Для заданной вероятности Р = 0,95 и числа измерений n = 7 по таблице коэффициентов. Стьюдента ( при К=6 ) установим значение коэффициента Стьюдента tp = 2,45.
Тогда доверительные границы случайной погрешности результата измерений, мм:
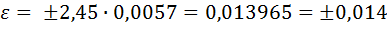
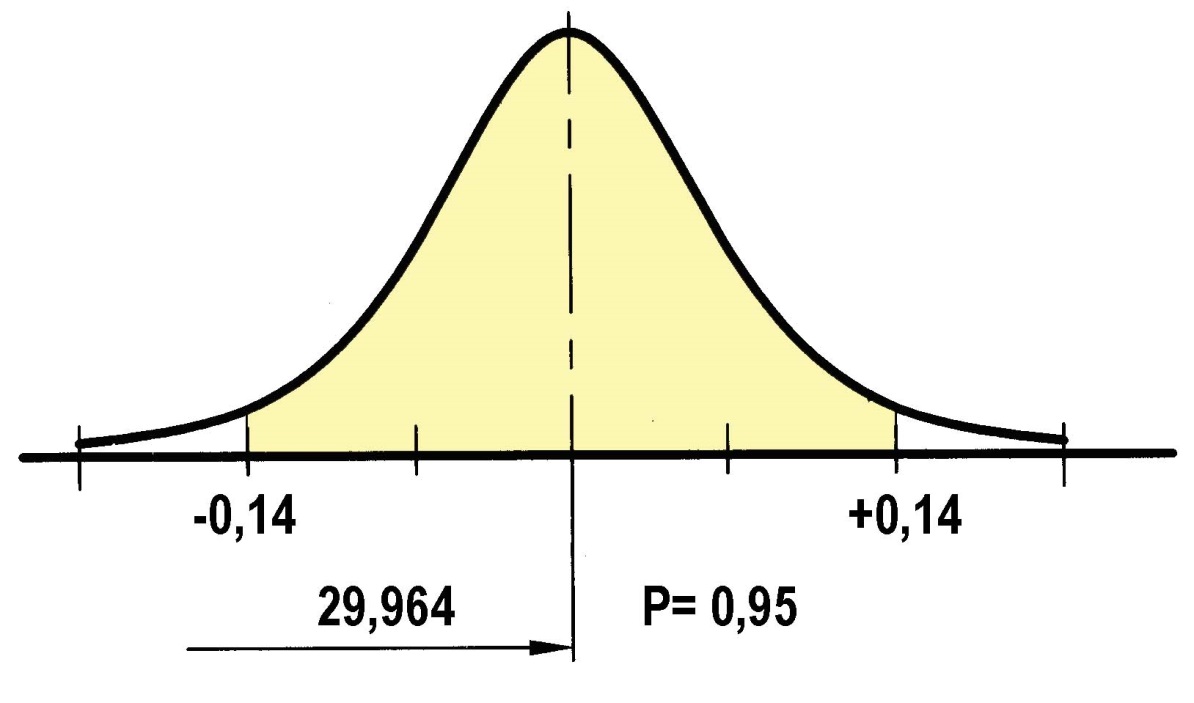
6. Результат измерений запишем в виде А = 29,964 ± 0,014, P=0,95.
Однократные измерения
Большинство технических измерений являются однократными. В производственных условиях их точность может быть вполне приемлемой. При однократных измерениях процедура измерений регламентируется заранее, с тем чтобы при известной точности средств измерений и условиях измерения погрешность не превзошла определенное значение, т.е. значения D и Р заданы исходно. Так как такие измерения выполняют без повторений, то нельзя отделить случайные погрешности, от систематических. Для оценки погрешности дают лишь ее границы с учетом возможных влияющих величин.
Однократные измерения возможны при следующих условиях:
- объем априорной информации об объекте измерений такой, что однократные измерения не вызывают сомнений;
-изучен метод измерения, его погрешности либо заранее устранены, либо оценены;
- метрологические характеристики средств измерений соответствуют установленным нормам.
При однократных измерениях возможно образование инструментальной, методической и субъективной погрешностей. Если последние погрешности две не превышают 15% погрешности средства измерений, тогда погрешность измерения принимают равной погрешности используемого средства измерений
Однократный отсчет показаний может тоже содержать промах. Во избежание промаха при выполнении однократных измерений рекомендуется повторять измерения 2-3 раза, приняв за результат среднее арифметическое.
В простейшем случае, если влияющие величины соответствуют нормальной области значений, погрешность результата прямого однократного измерения равна основной погрешности средства измерений Δ, определяемой по нормативно-технической документации. Тогда результат измерения записывают в виде
А = Хси ± Δси , Р,
где Хси - результат (среднее арифметическое значение из 2-3 единичных измерений), зафиксированный средством измерений.
Доверительная вероятность Р, как правило, составляет 0,95. При проведении измерений в условиях, отличных от нормальных, необходимо определять и учитывать пределы дополнительных погрешностей, вызванных имеющимися отличиями.
Пример. Произведены измерения длины L = 50 ± 0,3 мм стержня штангенциркулем ШЦ-П, основная погрешность которого составляет Δси = ± 0,05 мм. Получены следующие результаты: Х1 = 50,10 мм; Х2 = 50,20 мм; Х3 = 50,15 мм. Записать окончательный результат измерений в стандартной форме.
Среднее арифметическое измеряемого размера. 
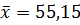
Результат измерения запишем в виде
А = 50,15 ± 0,05 ; 0,95.
При неизвестной же погрешности средства измерения оценка производится на основе СКО
Пример... При измерении размера вала Ø55u8( 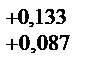 ) получены следующие результаты, мм:
) получены следующие результаты, мм:
х1=55,01; х2=55,13; х3=55,12; х4=55,12; х5=55,12.
Провести точную оценку результатов измерений:
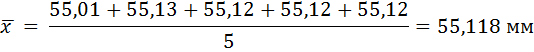
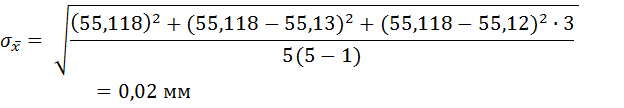
Таким образом, результат измерений
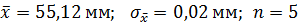
Если же, ввести доверительную вероятность Р= 0,95 то можно определить и доверительный интервал.
| <== предыдущая лекция | | | следующая лекция ==> |
| Измерение параметров электрических цепей | | | Нормативно-правовая база обеспечения единства измерений. |
Дата добавления: 2016-06-15; просмотров: 6524;











