Периодические граничные условия и их физический смысл.

Мы собираемся изучать поведение макроскопической системы, состоящей из молекул с числом порядка числа Авогадро N_A » 10²³ моль^–1. Даже в упрощенном двумерном случае нам пришлось бы решать 2N_A » 10²⁴ моль^–1 уравнений второго порядка, что в принципе невозможно из-за громадности такого числа. Интуитивно кажется, что можно обойтись рассмотрением числа частиц N << N_A в сосуде с жесткими стенками, но, взяв N не настолько большим, чтобы можно было иметь возможность решать необходимое количество уравнений на самых лучших ЭВМ. Но простые рассуждения показывают, что даже для современных ЭВМ продвинуться в данном направлении не так уж просто.

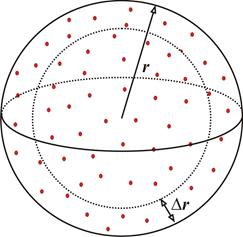
Рис. 4.4. Произвольная шаровая область с частицами.

Действительно, рассмотрим газ в сферическом сосуде радиуса r на рис. 4.4. Выделим в нем сферический слой толщиной Dr << r, но такой, что Dr >> l – толщины свободного пробега молекул. Объем V сферы равен V = 4/3pr³, а объем DV сферического слоя DV = 4pr²Dr. Доля d молекул, заключенных в слое составляет

.

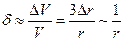Но N ~ V ~ r³, т.е. d ~ N ^–1/3. Если сравнить относительное изменение d при переходе с N = 10 к N = 1000, то получается изменение d менее чем в 5 раз. Расчет динамики 1000 молекул для современных ЭВМ остается трудоемкой задачей, и, поэтому малопривлекательным. К счастью сложившуюся трудность можно обойти следующим способом. Для этого снова рассмотрим N частиц в 2-мерном ящике (сосуде). Но теперь будем считать стенки ящика не физически реальными, а существующими условно, воображаемыми. Частицы могут свободно проходить через «стенки» ящика. В сущности, это означает, что из системы с N_A частиц мы выделяем фрагмент, который мы называем ящиком с числом частиц ~ 10…100. В действительности в выделенном фрагменте число N молекул не постоянно: оно случайно колеблется около некоторого среднего значения. Такого рода колебания называются флуктуациями. Чем больше ящик, т.е. чем больше N, тем меньше проявляют себя флуктуации, которые убывают как 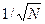– быстрее, чем влияние стенки сосуда. Ниже, считая число частиц в ящике постоянным, мы пренебрегаем флуктуациями.

Так как частицы могут свободно проходить через «стенки» ящика, нам необходимо выбрать алгоритм контроля общего числа частиц в ящике. Один из таких алгоритмов заключается в так называемых периодических граничных условиях. Чтобы понять, что это такое, рассмотрим элементарный пример движения двух частиц на отрезке (одномерный ящик) длиной L = 4 (рис. 4.5, а). Концы отрезка являются «стенками» одномерного ящика.

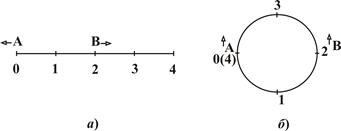
Рис. 4.5.Кажущаяся трансформация отрезка в окружность при периодических граничных условиях.

В какой-то момент времени t₁ частицы А и В находятся в точках с координатами x_A = 0 и x_B = 3. Стрелками показаны их направления движения. В следующий момент времени t₁ + Dt частица А вылетит из ящика. Будем считать, что в этот же момент времени эта же частица влетает с противоположной стороны x_A = 4 с той же скоростью, что и в момент вылета. Теперь уже частица А будет двигаться навстречу частице В. Нетрудно увидеть, что эту процедуру в случае N частиц можно выразить математически условиями:

если x_i < 0, то x_i ® x_i + L; (4.11)

если x_i > L, то x_i ® x_i – L, i = 1, 2, …, N.

Геометрическое содержание приведенных условий поясняется следующим образом. Мысленно свернем отрезок в кольцо. Тогда точки 0 и 4 совместятся. Учитывая проницаемость «стенок» ящика приходим к выводу, что теперь все движение как бы (!) совершается по кольцу, где нет границ, т.е. «стенок» (рис. 4.5, б). Условия (4.11), называемые периодическими граничными условиями, накладывают ограничения на измерение расстояния между частицами: вдоль кольца расстояние между ними не может превысить значения L/2. Поэтому при вычислении силы притяжения между частицами должны накладываться условия:

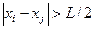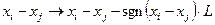если , то (4.12)

для всех i ¹ j,

где sgn – функция, значением которой является знак аргумента. Т.е. она принимает значение +1, если ее аргумент положителен, и –1 в случае отрицательного аргумента.

Возвратимся теперь к движению в двумерном «ящике». Движения вдоль координат происходят независимо друг от друга. Поэтому условия (4.11) и (4.12) остаются справедливыми и для координат частиц по оси y. Геометрическим образом получающихся в результате граничных условий области движения является тор (рис. 4.6).

Для частиц с координатами x_i, y_i заключенных в двумерный ящик со сторонами L_x, L_y периодические граничные условия имеют вид:

если x_i < 0, то x_i ® x_i + L_x; (4.13)

если x_i > L_x, то x_i ® x_i – L_x,

если y_i < 0, то y_i ® y_i + L_y;

если y_i > L_y, то y_i ® y_i – L_y,

i = 1, 2, …, N.

Эти условия отображают исходный прямоугольник на поверхность тора, не имеющего границ. Но ослабленное влияние границ прямоугольника теперь проявляется, как следствие принятых периодических граничных условий, в невозможности удаления двух произвольных частиц на расстояние не более чем на L_x/2 по оси x и на L_y/2 – по оси y:

если 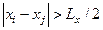, то 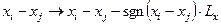; (4.14)

если 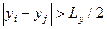, то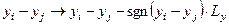

для всех i ¹ j.

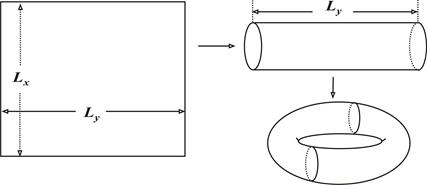
Рис. 4.6. Кажущаяся трансформация прямоугольника в тор при периодических граничных условиях.

Может показаться, что при «сворачиваний» отрезка в кольцо, а прямоугольника в цилиндр, а затем в тор, мы полностью избавились от влияния на динамику молекул границ – «стенок». На самом деле это не так. Условия (4.11), (4.12) только лишь минимизируют такого рода влияния, но не избавляют от них полностью. Это видно из того, что расстояния между любыми двумя частицами не может быть больше L_x/2 по координате x и L_y/2 – по координате y. По этой причине возникает не имеющее физического смысла взаимодействие между частицами, источник которого кроется в относительно слабом убывании потенциала с расстоянием. Это обстоятельство вынуждает проводить корректное моделирование так, чтобы размеры L_x, L_y были много больше средней длины свободного пробега частиц. Тогда эффект «стенок» становится ничтожно малым.

Обратим внимание на один важный аспект. Движения частиц по кольцу в одномерном случае и по поверхности тора – в двумерном случае, не являются физическими движениями, с которыми мы обычно сталкиваемся. Ведь в обоих случаях частицы должны были бы испытывать центробежную силу, прямо пропорциональной радиусу кольца или тора. Но на самом деле такой силы в уравнениях (4.10) нет, и она не привносится периодическими граничными условиями.