Определение рациональных способов раскроя материала.

В задачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Пред­положим, что из единицы материала можно изготовить заготов­ки нескольких видов. Способ раскроя единицы материала назы­вается рациональным (оптимальным по Парето), если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.

Пусть k — индекс вида заготовки, k = 1,.... q; i — индекс спо­соба раскроя единицы материала, i = 1,..., р; а_ik — количество (це­лое число) заготовок вида k, полученных при раскрое единицы материала <-м способом.

Приведенное определение рационального способа раскроя мо­жет быть формализовано следующим образом.

Способ раскроя v называется рациональным (оптимальным по Па­рето), если для любого другого способа раскроя i из соотношений а_ik ³ а_vk , k = 1, ..., q, следуют соотношения а_ik = а_vk, k = 1, ..., q.

2. Определение интенсивности использования рациональных спо­собов раскроя.

Обозначения:

j —индекс материала, j = 1,..., п;

k —индекс вида заготовки, k = 1, ..., q;

i — индекс способа раскроя единицы материала, i = 1,..., р;

а_ijk — количество (целое число) заготовок вида k, полученных при раскрое единицы j-го материала i-м способом;

b_k — число заготовок вида k в комплекте, поставляемом заказ­чику;

d_j — количество материала j-го вида;

x_ji — количество единицу j-го материала, раскраиваемых по i-му способу (интенсивность использования способа раскроя);

c_ji — величина отхода, полученного при раскрое единицы j-го материала по i-му способу;

у — число комплектов заготовок различного вида, поставля­емых заказчику.

Модель А раскроя с минимальным расходом материалов:

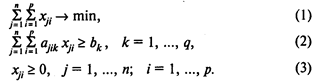
Здесь (1) — целевая функция (минимум количества использу­емых материалов);

(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(3) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являются ограничения (2).

Модель В раскроя с минимальными отходами:

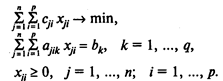
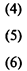
Здесь (4) — целевая функция (минимум отходов при раскрое ма­териалов);

(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(6) — условия неотрицательности переменных.

Модель С раскроя с учетом комплектации:

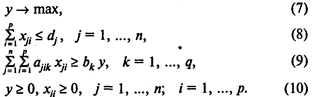
Здесь (7) — целевая функция (максимум комплектов, включающих заготовки различных видов);

(8) — ограничения по количеству материалов;

(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;

(10) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являются ограничения (9).

Примеры. Пример 1. Способы раскроя металлического стержня.

Определите все рациональные способы раскроя металлического стержня длиной 100 см на заготовки трех типов: длиной 20, 30 и 50 см. Укажите величину отходов для каждого способа.

Решение. Для данного материала и указанных заготовок су­ществует семь различных рациональных способов раскроя. Все они приведены в следующей таблице:

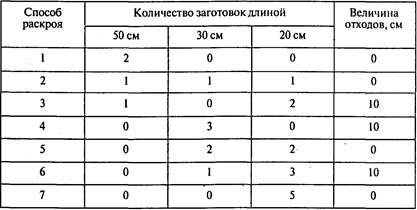
Пример 2. Способы раскроя куска кожи.

Определите все рациональные способы раскроя прямоугольного куска кожи размером 100 х 60 см на квадратные заготовки со сторо­нами 50,40 и 20 см и укажите величину отходов для каждого способа.

Решение. Для данного материала и указанных заготовок су­ществует шесть различных рациональных способов раскроя:

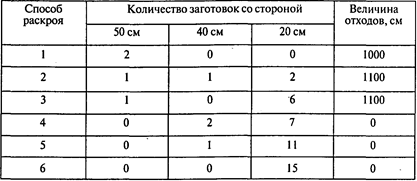
Пример 3. Изготовление парников из металлических стержней.

При изготовлении парников используется материал в виде ме­таллических стержней длиной 220 см. Этот материал разрезается на стержни длиной 120, 100 и 70 см. Для выполнения заказа тре­буется изготовить 80 стержней длиной 120 см, 120 стержней дли­ной 100 см и 102 стержня длиной 70 см.

Вопросы:

1. Сколько существует рациональных способов раскроя?

2. Какое минимальное количество материала следует разрезать, чтобы выполнить заказ?

3. Сколько способов раскроя следует использовать при выпол­нении заказа?

Решение. Определяем все рациональные способы раскроя ма­териала на заготовки. Таких способов оказывается пять:

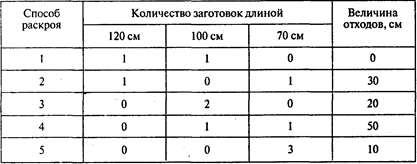
Используем модель А для одного вида материала. Тогда х_i — количество единиц материала, раскраиваемых по i-му способу.

Для ответа на второй и третий вопросы задачи получаем сле­дующую модель линейного программирования с критерием «ми­нимум общего количества используемого материала»:

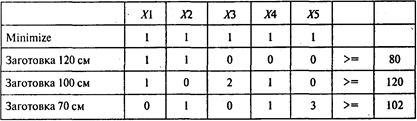
Решая задачу, получаем следующий результат:

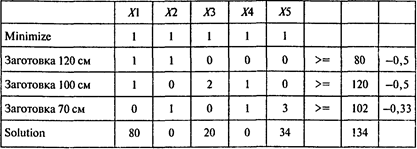
Ответы: 1. Пять способов. 2. 134 единицы материала. 3. Три из пяти рациональных способов раскроя.

Планирование финансов. Цели

В данной главе показаны возможности использования модели линейного программирования для решения некоторых задач плани­рования финансов. При определенных предположениях становит­ся возможным выбрать такие способы вложения денег под процен­ты, совокупность которых позволяет минимизировать первоначаль­ный вклад, необходимый для выплаты займа, или максимизировать доход. При решении задач финансового планирования можно учи­тывать риск и другие факторы, влияющие на выбор способов вло­жения денег.

После выполнения заданий, предлагаемых в этой главе, вы бу­дете уметь формулировать и использовать для экономического анализа следующие понятия:

• вклад;

• целевой фонд;

• балансовое ограничение;

• индекс риска по вкладу.

Модели

Модель А минимизации целевого фонда. Предположим, что в определенные моменты времени необходимо выплачивать извест­ные суммы денег по взятому ранее займу. Чтобы накопить эти суммы, можно заранее создать целевой фонд, а средства из этого фонда использовать для срочных вкладов. Каждый срочный вклад характеризуется моментом времени вложения, сроком погашения и доходностью. Задача состоит в том, чтобы определить минималь­ный размер целевого фонда и выбрать те виды срочных вкладов, которые следует использовать, чтобы сделать выплату по займу. Обозначения:

у — размер целевого фонда, создаваемого в нулевой момент времени;

t — текущий момент времени, t = 0, 1,.... Т;

d_t — размер выплаты по займу, которую надо произвести в мо­мент времени t (t = 1, ..., Т);

j —индекс срочного вклада, j = 1,..., п;

v_j — момент времени вложения по срочному вкладу j;

w_j — срок выплаты по срочному вкладу j;

r_j — доходность срочного вклада j (процент по вкладу);

х_j — объем вложений по срочному вкладу j.

Предполагается, что для любого срочного вклада j момент v_j времени вложения фиксирован. Если по срочному вкладу/сде­ланы вложения в размере х_j, то через w_j единиц времени вклад­чику выплачивается сумма (1 + r_j)х_j. Без ограничения общности можно считать, что для любого момента времени существует та­кой вклад, выплата по которому производится в следующий мо­мент времени. При этом доходность такого вклада может быть нулевая. Использование вклада с нулевой доходностью означает, что деньги остаются на руках у владельца.

Пусть G_t — множество индексов j, таких, что t= v_j, т.е. по вкладу j сделано вложение в момент времени t, Q_t — множество индексов j, таких, что t = v_j + w_j, т.е. по вкладу j получена выплата в момент времени t.

Заметим, что для любого t множества G_t и Q_t известны.

Тогда модель имеет следующий вид:

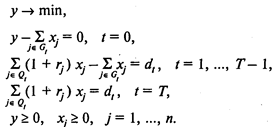
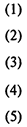
Здесь (1) — целевая функция (минимальный размер целевого фонда);

(2) —условие, характеризующее распределение целевого фонда по вкладам в нулевой момент времени;

(3) — соотношения, устанавливающие баланс между выпла­тами и вложениями;

(4) — условие, обеспечивающее выплату по займу;

(5) — условия неотрицательности переменных.

Модель В максимизации дохода. Предположим теперь, что вкладчик собирается делать вклады для того, чтобы через опреде­ленный период времени получить максимальный доход. Задача состоит в том, чтобы определить величину максимального дохода при фиксированном размере целевого фонда и выбрать те виды срочных вкладов, которые следует использовать.

Сохраним принятые ранее обозначения и введем новые:

z — размер дохода, который может получить вкладчик в мо­мент времени Т;

и_t— размер вклада в момент времени t (t = 0, 1,..., Т— 1).

Тогда модель имеет следующий вид:

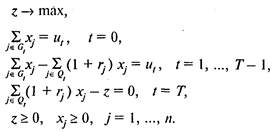
Здесь (6) — целевая функция (максимальная величина дохода);

(7) — условие, характеризующее распределение вклада в нулевой момент времени;

(8) — соотношения, устанавливающие баланс между вы­платами и вложениями;

(9) — условие, определяющее величину дохода;

(10)—условия неотрицательности переменных.

Примеры. Пример 1. Вложение денег под проценты.

Петр Перфилов — управляющий компанией, которая только что заключила контракт на покупку нового оборудования для кон­сервирования овощей. В соответствии с договором компания должна выплатить поставщику в общей сложности 750 тыс. руб. Причем 150 тыс. руб. необходимо уплатить через два месяца, а остальные 600 тыс. руб. — через шесть месяцев после того, как оборудова­ние будет поставлено и испытано. Петр считает, что сразу после подписания договора следует образовать целевой фонд и исполь­зовать эти средства для вложения денег под проценты. Посколь­ку такие инвестиции породят дополнительную наличность к тому времени, когда придется вносить деньги за оборудование, Петр понимает, что целевой фонд должен быть меньше чем 750 тыс. руб. А вот сколько именно — зависит от имеющихся возможностей инвестирования.

Проанализировав варианты, Петр решил сосредоточиться на 12 возможных способах вложения денег под проценты. Виды вкла­дов, их продолжительность, возможные сроки вложения и процен­ты по вкладу приведены в следующей таблице:

Данные о возможностях вложений и возврата денег (в руб.) представлены в следующей таблице:

С учетом этих возможностей необходимо минимизировать раз­мер целевого фонда, обеспечивающего оплату оборудования.

Вопросы:

1. Каков минимальный размер целевого фонда, позволяющий сделать необходимые выплаты?

2. Какова стоимость в начальный момент времени одного руб­ля, который надо выплатить в начале седьмого месяца (че­рез шесть месяцев)?

3. Какова стоимость в начальный момент времени одного руб­ля, который надо выплатить в начале пятого месяца (через четыре месяца)?

Решение. Введем следующие обозначения:

у — размер целевого фонда;

А_i — размер вклада вида А в месяце i;

B_i — размер вклада вида В в месяце i;

С_i — размер вклада вида С в месяце i;

D_i — размер вклада вида D в месяце i.

Так как в любой момент времени можно сделать вклад на один месяц, хранить деньги на руках невыгодно. С учетом этого усло­вия задача минимизации целевого фонда может быть описана сле­дующей моделью:

Целевая функция

у ® min

при условиях

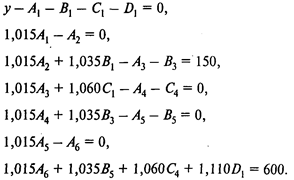
Эту модель можно представить в следующей, более наглядной форме:

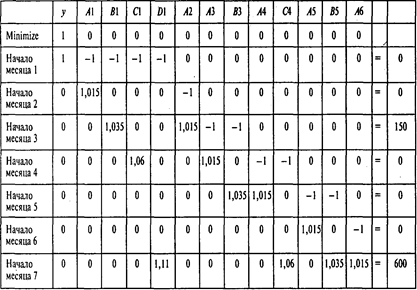
Проводя вычисления, получаем следующие результаты:

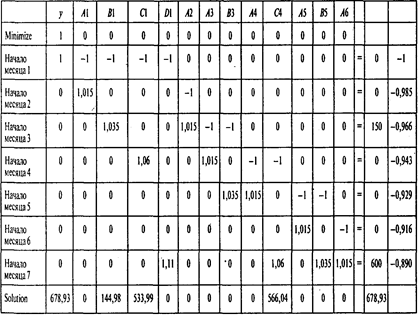
Следующая таблица содержит границы устойчивости по коэф­фициентам целевой функции:

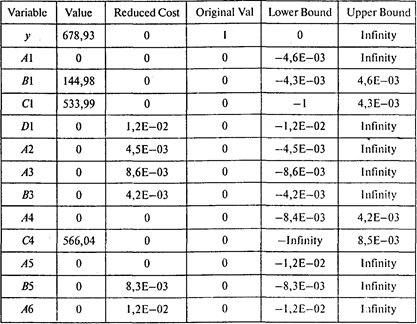
Далее приводятся границы устойчивости по правым частям ограничений:

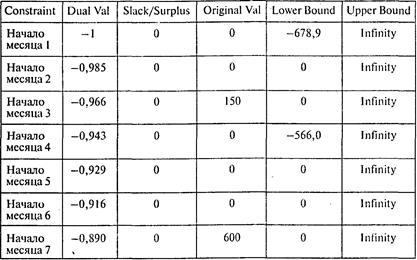
В этой модели особый интерес представляет интерпретация двойственных оценок. Например, двойственная оценка последнего ограничения равна —0,89. Это означает, что для выплаты через полгода одного дополнительного рубля необходимо увеличить размер целевого фонда на 0,89 руб. Таким образом, величина двой­ственной оценки есть стоимость одного рубля, выплачиваемого через полгода, приведенная к начальному моменту времени.

Ответы: 1.678,93 тыс. руб. 2.0,89руб. 3.0,929руб.