Оптимальное смешение. Цели
Модели
Введем обозначения:
п — количество выпускаемых продуктов;
т — количество используемых производственных ресурсов (например, производственные мощности, сырье, рабочая сила);
аij — объем затрат i-го ресурса на выпуск единицы j-й продукции;
сj — прибыль от выпуска и реализации единицы j-го продукта;
bi — количество имеющегося i-го ресурса;
хj — объем выпуска j-го продукта.
Формально задача оптимизации производственной программы может быть описана с помощью следующеймодели линейного программирования:
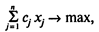 (1)
(1)
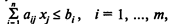 (2)
(2)
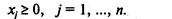 (3)
(3)
Здесь (1) — целевая функция (максимум прибыли);
(2) — система специальных ограничений (constraint) на объем фактически имеющихся ресурсов;
(3) — система общих ограничений (на неотрицательность переменных);
хj — переменная (variable).
Задача (1)—(3) называется задачей линейного программирования в стандартной форме на максимум.
Задача линейного программирования в стандартной форме на минимум имеет вид
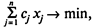 (4)
(4)
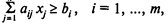 (5)
(5)
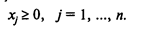 (6)
(6)
Вектор х = (x1, x2, ..., xn), компоненты хj которого удовлетворяют ограничениям (2) и (3) (или (5) и (6) в задаче на минимум), называется допустимым решением или допустимым планом задачи ЛП.
Совокупность всех допустимых планов называется множеством допустимых планов.
Допустимое решение задачи ЛП, на котором целевая функция (1) (или (3) в задаче на минимум) достигает максимального (минимального) значения, называется оптимальным решением задачи ЛП.
С каждой задачей ЛП связывают другую задачу ЛП, которая записывается по определенным правилам и называется двойственной задачей ЛП.
Двойственной к задаче ЛП (1)—(3) является задача
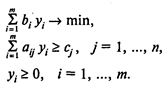
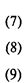
Соответственно, двойственной к задаче ЛП (7)—(9) является задача (1)—(3). Каждой переменной (специальному ограничению) исходной задачи соответствует специальное ограничение (переменная) двойственной задачи. Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.
Компонента 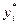 оптимального решения двойственной задачи (7)—(9) называется двойственной оценкой (Dual Value) ограничения
оптимального решения двойственной задачи (7)—(9) называется двойственной оценкой (Dual Value) ограничения 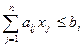 исходной задачи ЛП.
исходной задачи ЛП.
Пусть j = max ( 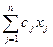 ), где хj — компонента допустимого решения задачи (1)—(3).
), где хj — компонента допустимого решения задачи (1)—(3).
Тогда при выполнении условий невырожденности оптимального решения имеют место следующие соотношения:
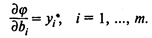
Изменим значение правой части bi одного основного ограничения (RHS) исходной задачи ЛП.
Пусть 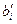 — минимальное значение правой части основного ограничения, при котором решение у* двойственной задачи не изменится. Тогда величину
— минимальное значение правой части основного ограничения, при котором решение у* двойственной задачи не изменится. Тогда величину 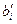 называют нижней границей (Lower Bound) устойчивости по правой части ограничения.
называют нижней границей (Lower Bound) устойчивости по правой части ограничения.
Пусть 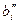 — максимальное значение правой части основного ограничения, при котором решение y* двойственной задачи не изменится. Тогда величину
— максимальное значение правой части основного ограничения, при котором решение y* двойственной задачи не изменится. Тогда величину 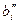 называют верхней границей (Upper Bound) устойчивости по правой части ограничения.
называют верхней границей (Upper Bound) устойчивости по правой части ограничения.
Изменим значение одного коэффициента сj целевой функции исходной задачи ЛП.
Пусть 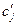 — минимальное значение коэффициента целевой функции, при котором оптимальное решение x* исходной задачи не изменится. Тогда величину
— минимальное значение коэффициента целевой функции, при котором оптимальное решение x* исходной задачи не изменится. Тогда величину 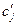 называют нижней границей устойчивости по коэффициенту целевой функции.
называют нижней границей устойчивости по коэффициенту целевой функции.
Пусть 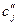 — максимальное значение коэффициента целевой функции, при котором оптимальное решение х* исходной задачи не изменится. Тогда величину
— максимальное значение коэффициента целевой функции, при котором оптимальное решение х* исходной задачи не изменится. Тогда величину 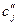 называют верхней границей устойчивости по коэффициенту целевой функции.
называют верхней границей устойчивости по коэффициенту целевой функции.
Примеры. Пример 1. Сколько производить?
Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, прибыль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов указаны в следующей таблице:
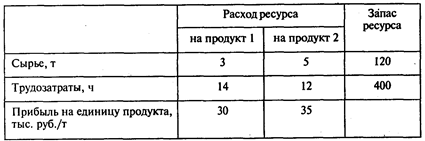
Вопросы:
1. Сколько продукта 1 следует производить для того, чтобы обеспечить максимальную прибыль?
2. Сколько продукта 2 следует производить для того, чтобы обеспечить максимальную прибыль?
3. Какова максимальная прибыль?
4. На сколько возрастет максимальная прибыль, если запасы сырья увеличатся на 1 т?
5. На сколько возрастет максимальная прибыль, если допустимый объем трудозатрат увеличится с 400 до 500 ч?
Решение. Пусть х1 — объем выпуска продукта 1 в тоннах, х2 — объем выпуска продукта 2 в тоннах. Тогда задача может быть описана в виде следующей модели линейного программирования:
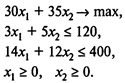
Используя пакет РОМ for WINDOWS (далее - POMWIN), исходную информацию для решения этой задачи можно представить в виде следующей таблицы:
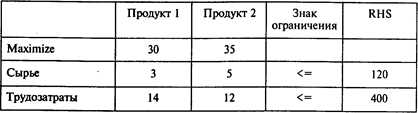
Решая эту задачу, получаем следующий результат:
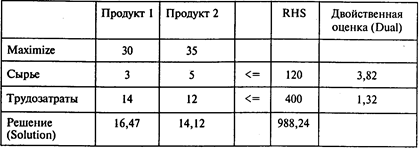
В нижней строке указан объем выпуска каждого продукта, удовлетворяющий ограничениям на ресурсы и обеспечивающий максимальную прибыль. Величина 988,24 — максимальное значение целевой функции.
Чтобы обеспечить максимальную прибыль, следует производить 16,47 т продукта 1 и 14,12 т продукта 2.
Максимальная прибыль равна 988,24 тыс. руб.
В правом столбце таблицы указаны двойственные оценки для каждого ограничения. Так, величина 3,82 показывает, что при увеличении запаса сырья на 1 т (до 121) максимальное значение целевой функции для нового оптимального плана увеличится по сравнению с 988,24 на 3,82 тыс. руб. Аналогично можно интерпретировать значение двойственной оценки 1,32 для второго ресурса.
Следующая таблица содержит дополнительную информацию, предоставляемую пакетом POMWIN:
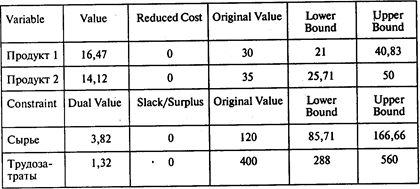
Два правых столбца таблицы — границы устойчивости по значениям коэффициентов целевой функции (верхняя часть таблицы) и правых частей ограничений (нижняя часть).
Так, в случае если прибыль, получаемая от реализации 1 т продукта 1, изменится, но останется в пределах от 21 до 40,83, количество продукта 1 в оптимальном плане не изменится.
В случае если запас сырья изменится, но останется в пределах от 85,71 до 166,66, двойственная оценка этого ресурса не изменится.
Соответственно, если допустимый объем трудозатрат изменится в пределах от 288 до 560 ч, двойственная оценка этого ресурса не изменится.
Если допустимый объем трудозатрат увеличится с 400 до 500 ч, то максимальная прибыль увеличится на 132 тыс. руб.
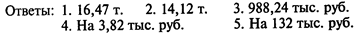
Пример 2. Производить или покупать?
Фирма производит два типа химикатов. На предстоящий месяц она заключила контракт на поставку следующего количества этих химикатов:

Производство фирмы ограничено ресурсом времени работы двух химических реакторов. Каждый тип химикатов должен быть обработан сначала в реакторе 1, а затем в реакторе 2. Ниже в таблице приведен фонд рабочего времени, имеющийся у каждого реактора в следующем месяце, а также время на обработку одной тонны каждого химиката в каждом реакторе:

Из-за ограниченных возможностей, связанных с существующим фондом времени на обработку химикатов в реакторах, фирма не имеет достаточных мощностей, чтобы выполнить обязательства по контракту. Выход заключается в следующем: фирма должна купить какое-то количество этих химикатов у других производителей, чтобы использовать эти закупки для выполнения контракта. Ниже приводится таблица затрат на производство химикатов самой фирмой и на закупку их со стороны:

Цель фирмы состоит в том, чтобы обеспечить выполнение контракта с минимальными издержками. Это позволит ей максимизировать прибыль, так как цены на химикаты уже оговорены контрактом. Другими словами, фирма должна принять решение: сколько химикатов каждого типа производить у себя, а сколько — закупать со стороны для того, чтобы выполнить контракт с минимальными издержками.
Вопросы:
1. Сколько химикатов типа 1 следует производить фирме?
2. Сколько химикатов типа 2 следует производить фирме?
3. Сколько химикатов типа 1 следует закупать со стороны?
4. Сколько химикатов типа 2 следует закупать со стороны?
5. Каковы минимальные издержки на выполнение контракта?
6. Следует ли изменить объем закупок химикатов типа 2 со стороны, если их цена возрастет до 75 тыс. руб. за тонну?
7. На сколько возрастут минимальные издержки, если фонд времени работы реактора 2 сократится с 400 до 300 ч?
Решение. Введем обозначения:
x1— количество продукта 1, производимого компанией;
z1 — количество продукта 1, закупаемого компанией;
x2 — количество продукта 2, производимого компанией;
z2 — количество продукта 2, закупаемого компанией.
Модель линейного программирования приведена в следующей таблице:
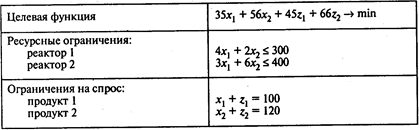
Условия неотрицательности переменных: 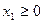 ;
; 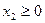 ;
; 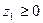 ;
; 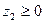 .
.
Таблица исходной информации для расчетов в POMWIN имеет следующий вид:
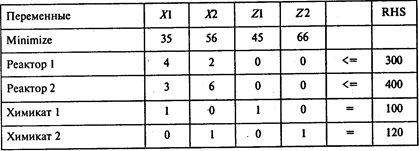
Результаты расчетов:
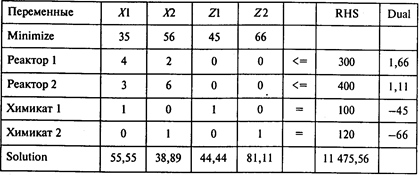
Таблица двойственных оценок и границ устойчивости:
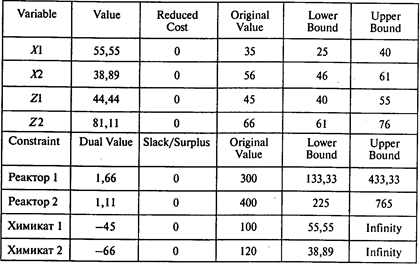
Из таблицы двойственных оценок и границ устойчивости видно, что в пределах изменения закупочной цены на химикат типа 2 от 61 до 76 (ее фактическое значение 66) оптимальный план не изменится.
Из таблицы также видно, что изменение ресурса времени работы реактора 2 в пределах от 225 до 765 не приведет к изменению двойственной оценки соответствующего ограничения.
Ответы: 1. 55,55 т. 2. 38,89 т. 3. 44,44 т. 4. 81,11 т.
5. 11 475,56 тыс. руб. 6. Нет, не следует.
7. Ha 111 тыс. руб.
Оптимальное смешение. Цели
В данной главе показаны возможности использования модели линейного программирования для решения задач оптимального смешения. Наряду с рассмотренной в главе 1 задачей планирования производства это одна из наиболее известных областей приложения модели линейного программирования. Модели оптимального смешения имеют много общего с моделями оптимального планирования производства. В то же время существуют и некоторые особенности.
После того как вы выполните задания, предлагаемые в этой главе, вы будете уметь формулировать и использовать для экономического анализа следующие понятия:
• смесь;
• ингредиент смеси;
• компонент смеси;
• рецепт смешения.
Модели
Важный класс прикладных оптимизационных задач образуют задачи о смесях. Такие задачи возникают при выборе наилучшего способа смешения исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количеством компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов и искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли.
Задачи оптимального смешения встречаются во многих отраслях промышленности (металлургия, парфюмерия, пищевая промышленность, фармакология, сельское хозяйство). Примерами задач о смесях могут служить определение кормового рациона скота на животноводческих фермах, составление рецептуры шихты на металлургическом производстве и т.п.
Рассмотрим сначала однопродуктовые модели оптимального смешения.
Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
хj — количество j-го ингредиента, входящего в смесь;
аij —количество i-го компонента в j-м ингредиенте;
сj —стоимость единицы j-го ингредиента;
bi — количество i-го компонента всмеси.
Модель А:
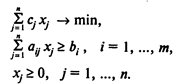
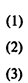
Здесь (1) — целевая функция (минимум затрат на получение смеси);
(2)— группа ограничений, определяющих содержание компонентов в смеси;
(3) — ограничения на неотрицательность переменных.
В задаче могут присутствовать также ограничения на общий объем смеси и ограничения на количество используемых ингредиентов. Эти группы ограничений, а также ограничения (2) характерны для задачи планирования производства, рассмотренной в главе 1.
Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
w — количество условий, отражающих содержание j-го ингредиента в смеси;
хj — количество j-го ингредиента, входящего в смесь;
аij — доля j-го компонента в j-м ингредиенте;
bi — минимально допустимая доля i-го компонента в смеси;
сj — стоимость единицы j-го ингредиента;
drj — коэффициент, отражающий r-е условие на содержание j-го ингредиента в смеси.
Модель В:
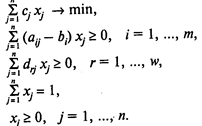
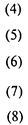
Здесь (4) — целевая функция (минимум затрат на получение смеси);
(5) — группа ограничений, определяющих содержание компонентов в смеси;
(6) — группа ограничении на содержание ингредиентов в смеси;
(7) — ограничение на количество смеси;
(8) — ограничения на неотрицательность переменных.
Ограничения (5) и (6) отличают задачу смешения от задачи оптимального планирования производства. Заметим, что значения правых частей этих ограничений равны нулю. Вектор х* с компонентами, являющийся решением этой оптимизационной задачи, называют рецептом приготовления смеси или рецептом смешения.
В многопродуктовых задачах ингредиенты используются для приготовления не одной, а нескольких смесей. При этом в качестве переменной xkj, такой задачи рассматривается количество ингредиента j, используемое для приготовления смеси k. Критерий задачи — максимизация прибыли.
Введем обозначения:
п — количество исходных ингредиентов;
т — количество компонентов в смеси;
w — количество условий, отражающих содержание j-го ингредиента в смеси;
s — количество смесей;
хkj — количество j-го ингредиента, входящего в k-ю смесь;
аij — доля i-го компонента в j-м ингредиенте;
bik — минимально допустимая доля i-го компонента в k-й смеси;
сj — стоимость единицы j-го ингредиента;
рk — стоимость единицы k-й смеси;
drkj — коэффициент, отражающий r-е условие на содержание j-го ингредиента в k-й смеси;
иj — количество имеющегося j-го ингредиента.
МодельС:
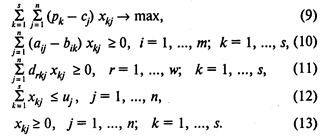
Здесь (9) — целевая функция (максимум прибыли);
(10) — группа ограничений, определяющих содержание компонентов в смеси;
(11) — группа ограничений на содержание ингредиентов в смеси;
(12) — ограничения на количество ингредиентов;
(13)— ограничения на неотрицательность переменных.
Примеры. Пример 1. Планирование производства на сочинском винзаводе.
Сочинский винзавод производит две марки сухого вина: «Черный лекарь» и «Букет роз». Оптовые цены, по которым реализуется готовая продукция, соответственно 68 и 57 руб. за литр. Ингредиентами для приготовления этих вин являются белое, розовое и красное сухие вина, закупаемые в Краснодаре. Эти вина стоят соответственно 70, 50 и 40 руб. за литр. В среднем на сочи иски и винзавод поставляется ежедневно 2000 л белого, 2500 л розового и 1200л красного вина.
В вине «Черный лекарь» должно содержаться не менее 60% белого вина и не более 20% красного. Вино «Букет роз» должно содержать не более 60% красного и не менее 15% белого.
Определите рецепты смешения ингредиентов для производства вин «Черный лекарь» и «Букет роз», обеспечивающие заводу максимальную прибыль.
Вопросы:
1. Какую максимальную прибыль можно получить за один день?
2. Сколько литров вина «Черный лекарь» следует производить ежедневно?
3. Сколько процентов белого вина должен содержать «Черный лекарь»?
4. Сколько литров вина «Букет роз» следует производить ежедневно?
5. Сколько процентов розового вина должен содержать «Букет роз»?
6. На сколько возрастет прибыль винзавода, если поставки красного вина удастся увеличить до 1300 л в день?
7. На сколько уменьшится прибыль винзавода, если поставки белого вина сократятся до 1800 л?
Решение. Пусть xkj — количество j-го ингредиента (j = 1, 2, 3), входящего в k-ю смесь (k = 1, 2). Например, x23 — количество красного вина, ежедневно используемого для приготовления вина «Букет роз». Тогда модель оптимального смешения имеет следующий вид.
Критерий максимизации прибыли:
(68 - 70)х11 + (68 - 50)x12 + (68 - 40)x13 + (57 - 70)x21 + + (57 - 50)x22 + (57 - 40)x22 ® max.
Ограничения на поставки ингредиентов:
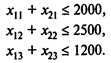
Ограничения, отражающие условия на содержание ингредиентов в смеси:
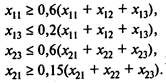
Последняя группа ограничений может быть преобразована следующим образом:
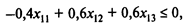
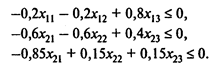
Кроме того, следует учесть ограничения на неотрицательность переменных.
Используя пакет POMWIN, исходную информацию для решения этой задачи можно представить в виде следующей таблицы:
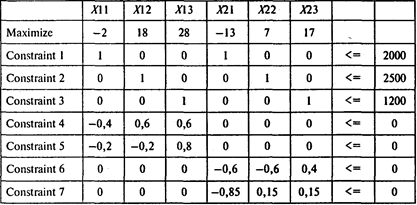
Решая эту задачу, получаем следующий результат:
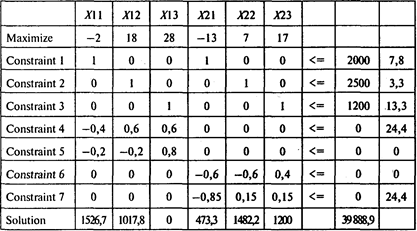
В следующей таблице содержится дополнительная информация о границах устойчивости решения по правым частям ограничений:
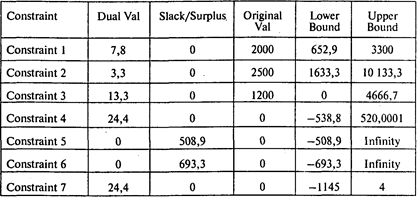
Таким образом, максимальная ежедневная прибыль винзавода достигает 39 888,9 руб. При этом производится 1526,7 + 1017,8 = 2544,5 л вина «Черный лекарь» и 473,3 + 1482,2 + 1200 = 3155,5 л вина «Букет роз». Поставляемые ингредиенты используются полностью.
Содержание белого вина в вине «Черный лекарь» составляет 1526,7/2544,5 = 0,6 (60%). Содержание розового вина в вине «Букет роз» составляет 1482,2/3155,5 = 0,47 (47%).
Если поставки красного вина удастся увеличить до 1300 л в день, то с учетом значения двойственной оценки 13,3 ограничения на объем поставок красного вина определяем, что прибыль увеличится на 13,3 • 100 = 1330 руб.
Заметим, что объем поставок остается в границах устойчивости решения. Если поставки белого вина сократятся до 1800 л в день, то с учетом значения двойственной оценки 7,8 ограничения на объем поставок белого вина определяем, что прибыль уменьшится на 7,8 • 200 = 1560 руб. Заметим, что объем поставок белого вина остается в границах устойчивости решения.
Ответы: 1. 39 889,9 руб. 2. 2544,5 л. 3. 60%.
4. 3155,5 л. 5. 47%. 6. На 1330 руб.
7. На 1560 руб.
Вопросы. Вопрос 1. Требуется определить объемы производства четырех видов лакокрасочных изделий. Рецепт производства каждого из них предполагает использование трех ингредиентов: олифы, красителя и белил. Объёмы поставок ингредиентов ограничены. Спрос на готовую продукцию не ограничен. Задача решается с целью максимизировать прибыль от реализации продукции.
Какое минимальное число переменных и ограничений содержит задача оптимального смешения?
Варианты ответов:
1) четыре переменные и три ограничения;
2) три переменные и четыре ограничения;
3) три переменные и двенадцать ограничений;
4) двенадцать переменных и три ограничения;
5) двенадцать переменных и четыре ограничения.
Вопрос 2. Для приготовления вина «Букет Молдавии» используется смесь из белого и красного сухих вин. Белого вина в готовой смеси должно быть не более 30%. Пусть х — количество белого вина, которое следует использовать для приготовления смеси; у — количество красного вина. Тогда условие на содержание ингредиентов в готовой смеси может быть формализовано следующим образом:
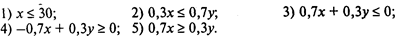
Вопрос 3. Для описания результатов, полученных при решении задачи оптимального смешения, может быть использована следующая фраза:
1) использованные для получения смеси компоненты не содержат необходимых ингредиентов;
2) рецепт смешения предполагает использование четырех ингредиентов;
3) для получения смеси надо использовать три компонента;
4) рецепт смешения предполагает использование трех компонентов;
5) рецепт смешения не предполагает использования этого компонента для приготовления смеси.
Вопрос 4. В задаче смешения исходными ингредиентами является бензин марок А, В и С, октановые числа которых 76, 93 и 98 соответственно. Октановое число смеси должно быть не менее 93.
Какое из неравенств правильно формализует это условие, если за х1, х2 и х3 принято предназначенное для смешения количество бензина марки А, В и С соответственно?
Варианты ответов:
1) 76 х1 + 93 х2 + 98 х3 ³ 93;
2) 76 х1 + 93 х2 + 98 х3 £ 93;
3) 5 х3 – 17 х1 ³ 0;
4) 17 х1 – 5 х3 £ 0;
5) 76 х1 + 98 х3 £ 93.
Вопрос 5. Ингредиенты j (j = 1,..., п) используются для приготовления смесей k (k = 1, ..., т). Пусть хjk — количество j-го ингредиента, входящего в k-ю смесь; сk — цена, по которой производитель продает готовую k-ю смесь; рj — цена, по которой закупается j-й ингредиент. Тогда критерии максимизации прибыли в задаче оптимального смешения будет иметь следующий вид:
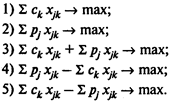
Дата добавления: 2022-07-20; просмотров: 130;










