Датчики положения и перемещения

<17 18 192021 22 23 >

5.6.1. Методы определения положения и перемещения

Существует два основных метода определения положения и измерения перемещения при помощи таких датчиков:

1) Датчик вырабатывает сигнал, являющийся функцией положения одной из его частей, связанных с подвижным объектом.

2) Датчик генерирует единичный импульс на каждом элементарном перемещении; положение и перемещение определяется подсчетом суммы или разности испущенных импульсов в зависимости от направления перемещения, в этом смысле эти датчики являются датчиками последовательных приращений.

5.6.2. Резисторные потенциометры

Потенциометр представляет собой резистор постоянного сопротивления R_n , по которому перемещается скользящий электрический контакт.

Этот контакт механически соединяется с деталью, перемещения которой он должен передавать.

В зависимости от формы резистора различают (см. рисунок 5.13):

- потенциометр линейного перемещения;

- потенциометр углового перемещения.

При этом зависимости текущего сопротивления R определяются выражениями:

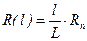- (5.43)

для потенциометра линейного перемещения l и

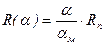- (5.44)

для потенциометра углового перемещения α.

Пример.

На рисунке 5.14 представлена схема для определения перемещения. Схема представляет собой следящий усилитель, размещенный на подвижном объекте.

Определение перемещения 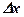производится путем использования измерительной информации, которая связана с изменением напряжения 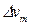на скользящем контакте вследствие его перемещения 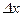от начального положения 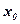. При этом используются очевидные зависимости:

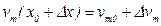(5.45)

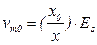и 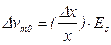(5.46)

где 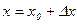- максимальное значение перемещения.

5.6.3. Индуктивные датчики

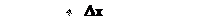В перемещение, которое измеряется, вовлекается один из элементов магнитного контура, который вызывает тем самым изменение потока через измерительную обмотку и соответствующий электрический сигнал.

Если подвижным элементом является ферромагнитный сердечник, то его перемещение при поступательном движении или вращении проявляется в изменении:

- коэффициента самоиндукции катушки (переменная индуктивность) или

- связи между первой и вторичной обмотками трансформатора, что приводит к изменению вторичного напряжения.

Магнитный контур с изменяемым зазором

На практике часто возникает задача определения различных зазоров в технических системах. Для этого используется магнитный контур. Соответствующая схема, поясняющая возможный способ определения зазоров с использованием такого контура, представлена на рисунке 5.15.

Существует зависимость для определения коэффициента самоиндукции.

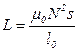, (5.47),

где 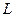- коэффициент самоиндукции;

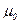- магнитная проницаемость;

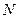- количество витков катушки;

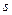- площадь сечения контура;

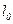- длина силовых линий в воздухе.

Перемещение 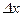обкладки приводит к изменению зазора на величину 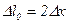, и индуктивность получает новое значение

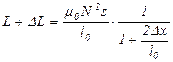Отсюда очевидны соотношения (с учетом соотношения (5.47)):

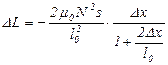и .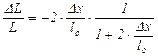

При 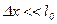имеем

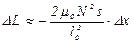и чувствительность датчика

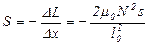Катушка с подвижным сердечником

Принципиальная схема катушки с подвижным сердечником представлена, на рисунке 5.16.

При последовательном объединении с коэффициентом и с коэффициентом

Для такой схемы (последовательное объединение различных участков) суммарный коэффициент индуктивности определяется соотношением

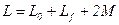, (5.48),

где 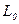- коэффициент индуктивности заполненного воздухом участка длиной l₀;

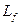- коэффициент индуктивности железного сердечника длиной l_f_;

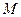- коэффициент взаимной индукции.

Очевидно, что перемещение Δl_f приводит к изменению 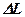. И, наоборот, зная 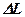и используя зависимость (5.48), легко определяется и искомое перемещение Δl.

5.6.4. Емкостные датчики

Такие датчики представляют собой плоские или цилиндрические конденсаторы, одна из обкладок которого испытывает перемещение, подвергаемое контролю, вызывая изменение емкости.

Емкость плоского конденсатора можно выразить как

,

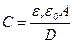где 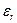- относительная проницаемость среды, заключенной между обкладками конденсатора;

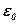- проницаемость среды;

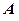- площадь поверхности обкладок;

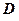- расстояние между обкладками.

Для цилиндрического конденсатора имеем

,

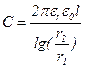где l - глубина погружения внутреннего цилиндра радиусом r₁ во внешний цилиндр радиуса r₂.

В случае плоского конденсатора перемещение обкладки может происходить либо:

- в собственной плоскости (A - переменная, D = const);

- либо перпендикулярно своей плоскости (A = const, D- переменная).

В случае цилиндрического конденсатора обкладка перемещается только параллельно оси (l = var).

Емкостные датчики просты, позволяют создавать надежные прочные конструкции.

Различают различные чувствительности датчика Sк перемещению x:

- чувствительность емкости

;

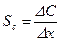- чувствительность импеданса

;

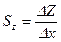- относительная чувствительность

.

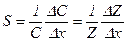Примеры

1. Конденсатор с переменой площадью обкладок

Таким конденсатором может быть:

- либо плоский с вращающейся обкладкой (см. рисунок 5.17, а)),

- либо цилиндрический с одной из обкладок, перемещающейся вдоль оси (см. рисунок 5.17, б)).

В обоих случаях емкость меняется линейно в зависимости от перемещений

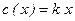. (5.54)

При этом:

- для плоского конденсатора из (5.49) следует

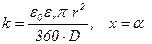, (5.55)

- для цилиндрического из (5.50) имеем

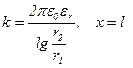. (5.56)

Соответственно чувствительности, определяемые по выражениям (5.51) - (5.53), находятся из выражений

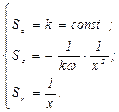(5.57)

2. Конденсатор с переменным зазором между обкладками

Схема такого конденсатора представлена на рисунке 5.18, где d – перемещение обкладки относительного начального зазора D₀.

Имеем

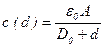, (5.57)

откуда вытекают соотношения для вычисления чувствительностей:

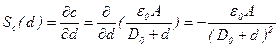; (5.58)

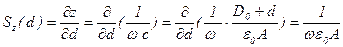; (5.59)

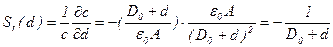. (5.60)

5.6.5. Цифровые датчики

Измерительную информацию, получаемую в аналоговом виде, можно обрабатывать с помощью цифровых схем.

Это становится возможным при использовании аналого-цифровых преобразователей (АЦП).

В случае перемещений – линейного или углового – можно создать датчик, измеряющий положение в цифровой форме.

Как и во всех приборах с цифровым преобразователем информации, при этом применяется квантование непрерывных значений информации.

5.6.6. Датчики близости

У таких датчиков нет механической связи между прибором и перемещением объектов.

Взаимодействие между ними, как функция их взаимного положения, устанавливается посредством поля, которым может служить:

- поле магнитной индукции для датчиков с переменным магнитным сопротивлением;

- электромагнитное поле для емкостных датчиков.

Достоинством датчиков близости является отсутствие механической связи, в связи с чем они имеют широкую полосу пропускания, высокую надежность.

Недостатки таких датчиков:

- малый диапазон измерений;

- нелинейность статической характеристики;

- зависимость показаний некоторых из них от формы, размеров и материала объекта и от параметров окружающей среды.

Датчики близости используются как в аналоговом режиме, так и в режиме цифровых кодов.

Датчики близости применяются при:

- измерении и стабилизации положения;

- контроле размеров;

- изучении (без помех) движения объектов малой инерционностью.

Датчики деформации

Знание механических напряжений, возникающих в конструкции при определенных условиях эксплуатации – главное условие обеспечения надежности функционирования конструкции.

Напряжение в материале вызывает деформацию, а соотношение между этими двумя величинами – напряжение – деформация – определяется из теории сопротивления материалов.

Измерение деформаций позволяет вычислить вызывающие их напряжения.

Датчики деформации могут служить также измерителями удлинений.

Наиболее часто используются резисторные датчики, которые приклеиваются на образец и деформируются вместе с ним.

5.7.1. Основные определения

Деформация ε – это отношение приращения Δl некоторого линейного размера к первоначальному значению этого размера:

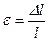. (5.61)

Упругая деформация – деформация, которая исчезает после устранения силы, ее вызвавшей.

Напряжение σ – это сила Fна единицу площади S сечения:

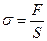. (5.62)

Предел упругости – максимальное напряжение, не вызывающее остаточно деформации.

Закон Гука: в области упругости деформация ε пропорциональна напряжению σ

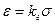. (5.63)

Модуль Юнга Y – определяет деформацию в направлении действия силы

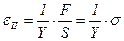. (5.64)

Коэффициент Пуассона ν определяет деформацию, перпендикулярную направлению действия силы:

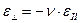. (5.65)

В области упругости имеет место соотношение .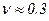

5.7.2. Основные положения

Резисторные датчики являются пассивными, т.к. они преобразуют в изменение сопротивления их собственную деформацию, практически равную деформации образца в области закрепления датчика.

Такой датчик представляет собой сетку из нитевидных проводников (см. рисунок 5. 19).

Сопротивление датчика определяется выражением

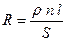, (5.66)

где 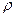- удельное сопротивление проводника;

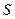- площадь поперечного сечения нити;

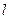- длина нитевидного элемента;

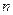- количество элементов.

Под действием деформации сопротивление датчика изменяется на 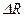. Его значение определяется можно получить из выражения (5.66) путем следующих преобразований:

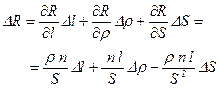. (5.67)

Разделив левую и правую части полученного выражения (5.67)на начальное значение сопротивления, определяемого выражением (5.66), легко получим:

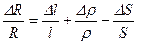. (5.68)

Продольные деформации нити приводят к изменению ее поперечных размеров - сторон a, b (если сечение прямоугольное) или диаметра d (если сечение нити случае круглое).

Очевидно, что поперечная деформация пропорциональна продольной, следовательно, имеют место соотношения:

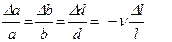, (5.69)

где 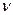- коэффициент Пуассона.

Используя выражения для площади сечения нити 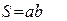(в случае прямоугольного сечения) и 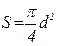(в случае круглого сечения), а также выражение (5.69), можно получить еще одну связь между поперечной и продольной деформациями – между изменением площади сечения 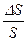нити и продольной деформацией :

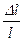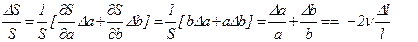- (5.70)

в случае плоского сечения нити и

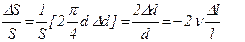- (5.71)

в случае круглого сечения нити.

Для металлических датчиков используется еще формула Бриджмена, связывающая изменение удельного сопротивления с изменением объема:

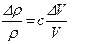, (5.72)

где c – константа Бриджмена.

Поскольку имеет место

,

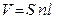то после очевидных преобразований можно получить

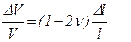. (5.73)

Из соотношения (5.72), используя последнее соотношение, получим

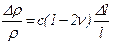, (5.74)

Далее из (5.68) с учетом (5.74) и (5.71) имеем

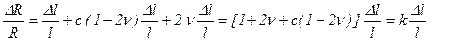, (5.75)

где

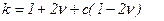. (5.76)

Учитывая, что 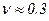, , 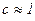получим 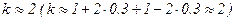, т.е. коэффициент преобразования металлического датчика можно принять .

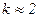Для полупроводниковых датчиков удельное сопротивление зависит от напряжения 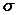и от коэффициента пъезорезистивности π.

Соответствующее выражение имеет вид:

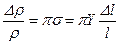. (5.77)

Следовательно, для полупроводникового датчика изменение сопротивления можно записать по аналогии (5.75) в виде

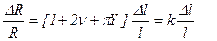, (5.78)

где

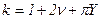. (5.79)

Обычно имеет место 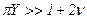. Поэтому на практике коэффициент преобразования принимают

.

<17 18 192021 22 23 >

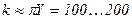Дата добавления: 2021-12-14; просмотров: 382;

Поиск по сайту

Узнать еще