Лекция 3. Расчет систем из упругоползучего материала
При наличии длительных нагрузок или несиловых воздействий[1] в материале конструкции развиваются, кроме так называемых мгновенных упругопластических деформаций, также деформации ползучести.
Иногда соответствующие задачи называются реологическими.
Теории, описывающие деформационные зависимости для таких случаев (процессы деформирования, развивающиеся во времени) могут быть объединены в две группы.
В первой группе определяющие соотношения включают напряжения, деформации и их производные по времени. Эти более простые теории, иногда называемые структурными теориями вязкоупругопластичности, приводят к расчетным методам, которые легче реализуются программно. Однако, для расчета объектов строительства они имеют ограниченное применение, так как для таких материалов, как бетон и древесина, не найдены соотношения этой группы, достаточно адекватно описывающие поведение таких конструкционных материалов; в то же время, именно для конструкций из этих материалов, в первую очередь, и необходим анализ их работы во времени. Только в последнее время начаты более детальные исследования процессов деформирования отдельных элементов структуры бетона с использованием соотношений этой группы; объем эмпирических материалов весьма мал и до нормирования расчетных параметров еще не доведен.
Во второй группе определяющие соотношения включают зависимости напряжений или деформаций от всей предыстории процесса в явном виде. В рамках теорий этой группы процесс длительного деформирования материала с учетом его старения (изменения деформативных свойств во времени) при достаточно низких напряжениях в случае одноосного напряженно-деформированного состояния можно описать линейными интегральными соотношениями (интегральные члены отражают влияние предыстории процесса):
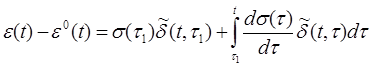 (3.1)
(3.1)
или, в более удобной форме с интегралом Стильтьеса –
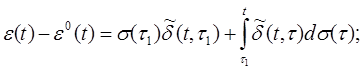 (3.1I)
(3.1I)
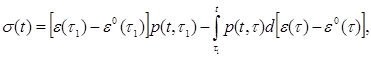 (3.2)
(3.2)
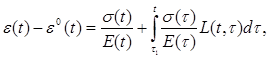 (3.3)
(3.3)
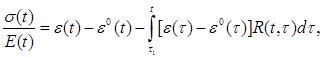 (3.4)
(3.4)
где e(t), e(t), s(t), s(t) – деформации и напряжения в материале в момент времени t (время наблюдения) или в предшествующие ему моменты времени t1 £ t £ t (время приложения воздействия), причем функции e(t), s(t) описывают “историю” процесса; 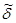 (t,t) – функция, описывающая изменение во времени полных удельных деформаций материала от единичного изменения напряжений в момент времени t, остающихся после этого постоянными –
(t,t) – функция, описывающая изменение во времени полных удельных деформаций материала от единичного изменения напряжений в момент времени t, остающихся после этого постоянными –
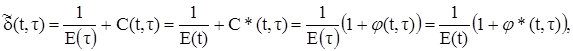
откуда видно суммирование мгновенной 1/Е и длительной С(t,t) частей; р(t,t) – функция, описывающая изменение во времени полных удельных напряжений (напряжений в момент времени t от единичного изменения деформаций в момент времени t, остающихся после этого постоянными) –
p(t,t) = E(t) + r(t,t)=E(t)+r*(t,t)=E(t)[1+y(t,t)]=E(t)[1+y*(t,t)],
причем r(t,t) < 0, r*(t,t) < 0, 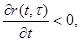 что свидетельствует о затухании (релаксации) напряжений во времени при стационарных деформациях (r(t,t)<0,
что свидетельствует о затухании (релаксации) напряжений во времени при стационарных деформациях (r(t,t)<0, 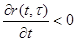 ) и о том, что в любой момент времени t действительные напряжения меньше упругих (r*(t,t)<0); L(t,t), R(t,t) – “наследственные функции”, называемые соответственно ядром ползучести и ядром релаксации; t1 – момент начала процесса; e0 – вынужденные деформации несиловой природы (температурные, усадочные, от неравномерной осадки опор и т.п.).
) и о том, что в любой момент времени t действительные напряжения меньше упругих (r*(t,t)<0); L(t,t), R(t,t) – “наследственные функции”, называемые соответственно ядром ползучести и ядром релаксации; t1 – момент начала процесса; e0 – вынужденные деформации несиловой природы (температурные, усадочные, от неравномерной осадки опор и т.п.).
Уравнения (3.1), (3.3) удобны при расчете систем методом сил, (3.2), (3.4) - методом перемещений.
При расчете объектов, материал которых претерпевает деформации ползучести, возникает ряд задач, интересных с теоретической точки зрения и важных практически; они связаны, например, с учетом таких факторов, как неоднородность системы ( в частности – наличие армирования, временная неоднородность при возведении монолитных железобетонных сооружений); изменение геометрии во времени (наращивание по высоте при возведении и по толщине – при усилении); сильный нагрев, приводящий к изменению свойств материала и усложнению наследственных функций; большие перемещения и потеря устойчивости; нелинейная ползучесть; наличие арматуры и образование трещин. Однако, эти задачи выходят за рамки настоящего конспекта, нацеленного на введение студента в проблематику и ознакомление с самыми элементарными понятиями.
Для расчета стержневых систем соотношения (3.1’) и (3.2) простым интегрированием левой и правой частей (умноженных на dy или ydy) по площади сечения с учетом гипотезы Бернулли могут быть приведены к виду (принимая равенство мгновенного и длительного коэффициентов поперечных деформаций и их постоянство во времени):
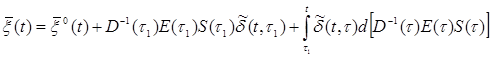 =
=
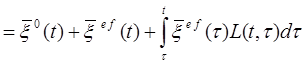 (3.5)
(3.5)
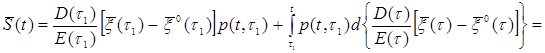
= 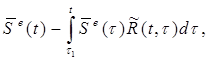 (3.6)
(3.6)
где 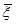 (е) = (e(t), g(t), æ(t))T – вектор-столбец деформаций (осевой, сдвиговой и изменения кривизны стержня); верхний индекс (ef) обозначает деформации упруго-мгновенной задачи, то есть, деформации, определяемые при заданных (действительных) напряжениях в предположении упругой работы материала;
(е) = (e(t), g(t), æ(t))T – вектор-столбец деформаций (осевой, сдвиговой и изменения кривизны стержня); верхний индекс (ef) обозначает деформации упруго-мгновенной задачи, то есть, деформации, определяемые при заданных (действительных) напряжениях в предположении упругой работы материала;
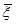 0 – вектор вынужденных деформаций; здесь учтено равенство мгновенных и длительных коэффициентов поперечных деформаций и их постоянство во времени, из которого следует E(t)/E(t) = G(t)/G(t);
0 – вектор вынужденных деформаций; здесь учтено равенство мгновенных и длительных коэффициентов поперечных деформаций и их постоянство во времени, из которого следует E(t)/E(t) = G(t)/G(t);
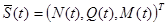 – вектор-столбец внутренних усилий в сечении; верхний индекс (е) свидетельствует о том, что соответствующие усилия определяются как в упругом теле (с учетом вынужденных деформаций) при заданных (действительных) деформациях;
– вектор-столбец внутренних усилий в сечении; верхний индекс (е) свидетельствует о том, что соответствующие усилия определяются как в упругом теле (с учетом вынужденных деформаций) при заданных (действительных) деформациях;
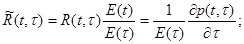
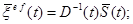
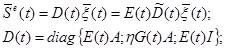
E(t)– модуль упругости материала; G(t) – его модуль сдвига;
h = 1/a – коэффициент, учитывающий неравномерность распределения касательных напряжений в сечении; A, I – площадь и момент инерции сечения.
Соотношения (3.5), (3.6) могут быть использованы как в рамках канонических методов, так и в случаях конечноразностной или конечноэлементной дискретизации в сочетании с вариационными методами.
Для разработки методов расчета рассматриваемых систем необходимо решить две задачи – научиться составлять разрешающие уравнения и предложить методы решения этих уравнений.
Составление разрешающих уравнений осуществляется различным способами; в частности, можно указать три из них:
1) классическими методами строительной механики (методы сил, перемещений, смешанный);
2) вариационными методами в сочетании с известными дискретными моделями несущих систем (конечноразностной, конечноэлементной), которые также приводят к уравнениям в усилиях (метод сил), в перемещениях (метод перемещений) или в усилиях и перемещениях (смешанный метод);
3) с использованием некоторых принципов механики, установленных для реологических систем и позволяющих свести решение реологических задач к задачам расчета упругих систем.
Рассмотрим обобщение классического метода сил на случай стержневой системы, выполненной из упругоползучего однородного материала. Примем традиционную гипотезу о возможности пренебречь влиянием нормальных и поперечных сил на эпюру изгибающих моментов. Одновременно учтем, что для упругоползучего тела справедлив принцип наложения воздействия.
В статически определимой основной системе деформативные свойства материала не влияют на ее напряженное состояние, которое полностью определяется условиями равновесия, и «единичные» эпюры изгибающих моментов одинаковы для упругих и реологических систем (пока влиянием перемещений и деформаций на условия равновесия можно пренебречь). С учетом этого обстоятельства эпюра изгибающих моментов в системе M(x,t) может быть представлена в виде:
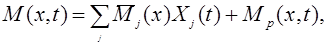 (3.7)
(3.7)
где 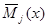 – j-ая «единичная» эпюра изгибающих моментов; Xj(t) – значение j-ой неизвестной (реакции j-ой связи) в момент времени t;
– j-ая «единичная» эпюра изгибающих моментов; Xj(t) – значение j-ой неизвестной (реакции j-ой связи) в момент времени t;
Mp (x,t) – «грузовая» эпюра изгибающих моментов в момент времени t, которая изменяется во времени только в следствие изменения нагрузок и воздействий.
Выделив из (3.5) третью компоненту (æ cлева и M справа) и не рассматривая для простоты вынужденные деформации, получим:
 æ(t)
æ(t) 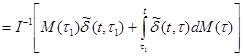 (3.5I)
(3.5I)
Подставим (3.7) в (3.5I): 
æ 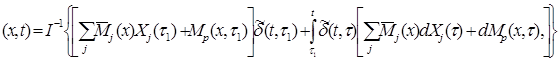 (3.8)
(3.8)
Теперь мы можем определить подлежащее приравниванию нулю взаимное смещение концов перерезанной j-ой лишней связи по формуле
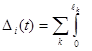 æ(x,t)
æ(x,t) 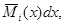 (3.9)
(3.9)
где k – номер участка; ℓk – его длина.
Подставим (3.8) в (3.9) и изменим порядок суммирований и интегрирования, а также заменим
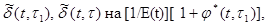 [1/E(t)][1+j*(t,t)]:
[1/E(t)][1+j*(t,t)]:
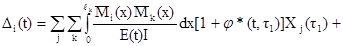
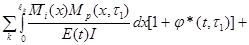
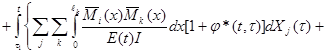
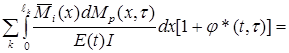
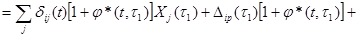
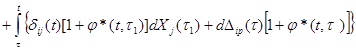 (3.10)
(3.10)
Это – i-ое каноническое уравнение метода сил для системы изгибаемых стержней из упругоползучего материала.
Обозначив матрицу податливости заданной системы при условии ее выполнения из упругого стареющего материала на момент времени t через 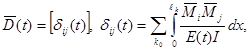 а столбец свободных членов – через F(t)=[Di(t)],
а столбец свободных членов – через F(t)=[Di(t)], 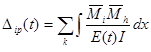 и столбец неизвестных X(t) = [Xi(t)], можно (3.10) записать в виде
и столбец неизвестных X(t) = [Xi(t)], можно (3.10) записать в виде
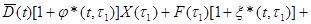
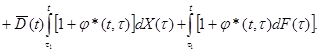 (3.11)
(3.11)
Решив интегральное уравнение (3.11), можно подставить X(t) в (3.7) и получить эпюру изгибающих моментов M(x,t).
Другой вариант разрешающего интегрального уравнения можно получить, если воспользоваться в качестве определяющего соотношения вторым вариантом формулы (3.5):
æ 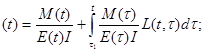 (3.5II)
(3.5II)
æ 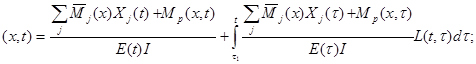 (3.8I)
(3.8I)
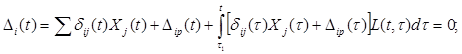 (3.10I)
(3.10I)
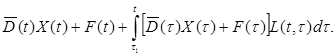 (3.11I)
(3.11I)
Это – матричное интегральное уравнение Вольтерра второго рода.
Для метода перемещений на основании изложенных далее теорем 1 и 2 созданное в момент времени t единичное смещение
j-ой - связи Zj = 1, наложенной при образовании основной системы, вызовет в момент времени t, согласно (3.6), изгибающий момент:
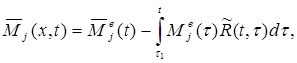 (3.12)
(3.12)
а грузовое состояние тождественно грузовому состоянию упругой системы:
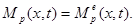 (3.13)
(3.13)
Окончательная эпюра:
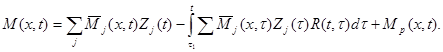 (3.14)
(3.14)
Реакцию i-ой опоры, введенной при образовании основной системы и подлежащей приравниванию нулю, можно определить также с использованием интеграла Мора (и способа Верещагина), если учесть, что “единичные” эпюры изгибающих моментов отвечают единичным угловым и линейным смещениям наложенных при образовании основной системы связей, а «грузовая» эпюра отвечает такой статически неопределимой основной системе, где среди прочих обязательно отброшена та связь (i-ая), реакция которой определяется:
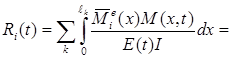
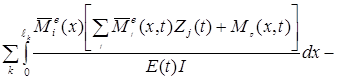
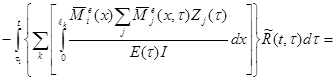
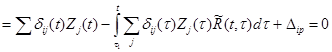 (3.15)
(3.15)
Таким образом, каноническая система уравнений классического метода строительной механики (метода сил либо метода перемещений) может быть записана в виде
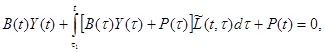 (3.16)
(3.16)
либо
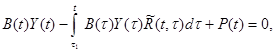 (3.17)
(3.17)
либо
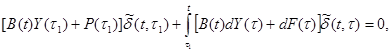 (3.18)
(3.18)
где B(t) – матрица коэффициентов для упругой системы; Y(t) – вектор неизвестных.
В любом случае это – интегральное матричное уравнение Вольтерра второго типа.
Аналогичный вид имеют разрешающие уравнения, полученные вариационным методом.
Для решения таких уравнений применяются различные численные методы: Боголюбова-Крылова (конечных сумм), итерированных ядер, интегральных преобразований (операционное исчисление) и др.
Чаще всего применяется метод конечных сумм. Продемонстрируем идею этого метода на примере уравнения (3.17). Приведем его к виду:
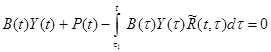 (3.19)
(3.19)
Первые два слагаемых этого уравнения соответствуют работе упругой системы. Последнее (интегральное) слагаемое отражает влияние истории загружения и является особенностью реологических задач. Этот интеграл в общем случае приходится брать численно; для простоты применим формулу трапеций (она дает достаточно большую погрешность и обычно применяются другие формулы):
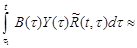
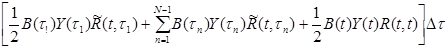 , (3.20)
, (3.20)
где tn =t1 +( n-1)Dt; t =t1 + NDt.
Здесь первые два слагаемых включают значения вектора неизвестных Y(t1) и Y(tn) при n < N в предшествующие моменты времени, последнее – значение этого же вектора в момент времени t, для которого выполняется расчет; подставим (3.20) в (3.19) и перегруппируем слагаемые:
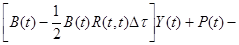
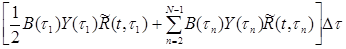 (3.21)
(3.21)
Коэффициент при Y(t) можно считать новой матрицей коэффициентов B*(t), а последнее слагаемое, включающее только предшествующие значения неизвестного – некоторой дополнительной фиктивной нагрузкой.
Полученное уравнение будем решать шаговым методом
(B*(t)=B(t)[E– 1/2 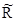 (t,t)Dt]):
(t,t)Dt]):
B(t1)Y(t1)+P(t1) = 0 (3.22)
Y(t1) = – B-1(t1)P(t1) (3.23)
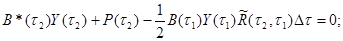 (3.24)
(3.24)
Y(t1) определен на предшествующем шаге и
Y(t2)=– [B*(t2)]–1[P(t2) – DPф(t1)] (3.25)
На каждом последующем шаге
B*(tm)Y(tm) + P(tm) – DPф(tm-1) = 0, (3.26)
где 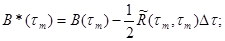 (3.27)
(3.27)
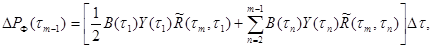 (3.28)
(3.28)
причем Y(tn) при n ≤ m – 1 все уже определены на предыдущих шагах вычислительного процесса.
В таком общем виде метод требует значительных ресурсов памяти ЭВМ (хранение вектора неизвестных на всех шагах по времени) и высокого быстродействия. Эти требования могут быть резко снижены в случае применения известного приема – аппроксимации заданного ядра вырожденным:
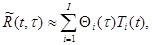 (3.29)
(3.29)
включающем I произведений (обычно 3…6).
При этом, так как tm не изменяется при изменении n:
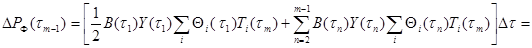
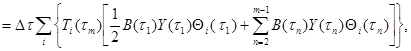 (3.30)
(3.30)
и вместо запоминания N значений вектора Y(tn) необходимо запомнить на каждом шаге только I сумм
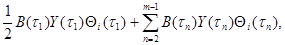 (3.31)
(3.31)
которые определяются в режиме накопления.
Применение классических методов строительной механики достаточно сложно и может быть оправдано только в случаях, когда материал не удовлетворяет изложенным выше предпосылкам, имеются упругоподатливые опоры, система неоднородна, в частности, имеет упругое либо упругопластическое армирование.
Аналогичное решение получаем при использовании вариационных методов.
Теперь ознакомимся с принципами механики, позволяющими свести решение реологической задачи к решению некоторой соответствующей ей задачи расчета упругой системы.
В основном это принципы соответствия. Наиболее ранний из них – принцип Вольтерра. Этот принцип подразумевает составление разрешающих уравнений путем замены в разрешающих уравнениях упругой задачи упругих констант некоторыми операторами с вычислением функций этих операторов и последующим решением полученного операторного уравнения. Первоначальный вариант метода относился только к однородным системам, выполненным из нестареющего материала, подчиняющегося закону линейной ползучести, затем он неоднократно обобщался на более широкий класс задач. Его применение требует владения нетривиальным математическим аппаратом, выходящим за пределы курса высшей математики для втузов, поэтому здесь это напраление не развивается.
Кроме принципа Вольтерра, можно отметить два принципа соответствия (для двух частных задач), иногда называемые теоремами Арутюняна (ранее в более частной постановке они были установлены другими авторами). Эти теоремы справедливы, если коэффициент поперечной деформации постоянен во времени, одинаков для кратковременного и длительного процессов, ползучесть линейна. Сформулируем их для однородных стержневых систем.
Теорема 1. Если напряженно-деформированное состояние системы вызвано только нагрузками, а опоры не смещаемы (то есть, отсутствуют податливые защемления и шарнирная опора) или выполнены из того же материала, что и заданная система, то внутренние усилия в системе S (t,x) тождественны внутренним усилиям, определенным в предположении упругой работы материала, а деформации определяются интегральными уравнениями
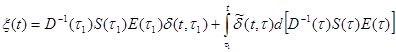 , (3.32)
, (3.32)
или
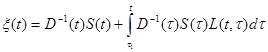 . (3.33)
. (3.33)
Теорема 2. Если напряженно-деформированное состояние системы вызвано только вынужденными деформациями и перемещениями, а те опоры, которые в процессе деформирования системы остаются несмещаемыми, либо являются абсолютно жесткими, либо выполнены из того же материала, что и заданная система, то полные деформации x(t) и перемещения системы тождественны полным деформациям и перемещениям, определнным в предположении упругой работы материала, а внутренние усилия определяются интегральными уравнениями:
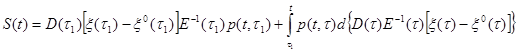 , (3.34)
, (3.34)
или
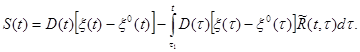 (3.35)
(3.35)
Так как в условиях линейной ползучести справедлив принцип наложения воздействий, результат одновременной реализации нагрузок и воздействий, вызывающих появление вынужденных деформаций, может быть рассчитан совместным применением обеих теорем.
Таки образом, эти две теоремы позволяют решать достаточно широкий класс задач при произвольных нагрузках и воздействиях; однако, этот класс задач ограничен сформулированными выше условиями.
Для уравнения (3.35) в случае стационарных вынужденных деформаций известно решение, имеющее вид
M(t) = Me(t)H(t,t1) = Me(t1)H*(t,t1), (3.36)
где 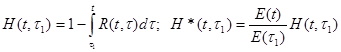 .
.
В случае нестационарных воздействий используется принцип наложения:
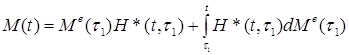 (3.37)
(3.37)
Для отдельных стандартных режимов загружения бетона был предложен метод трансформированных диаграмм. Например, при заданном изменении e(t) из (3.2) следует однозначная зависимость s(t) от деформации e(t), что может быть истолковано, как трансформированная диаграмма s – e; в случае обобщения (3.2) на область нелинейной ползучести эта диаграмма может быть продолжена до высоких уровней деформаций, и расчет предлагается выполнять как для кратковременного загружения физически нелинейной системы с заданной диаграммой s – e.
ЛИТЕРАТУРА
1.Качанов Л.М. Основы теории пластичности. – М.: Наука, 1969.–420 с.
2.Ржаницын А.Р. Строительная механика. –М.: Высшая школа, 1982. – 400с.
3.Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975. –541 с.
4. Арутюнян Н.Х., Колмановский В.Б. Теория ползучести неоднородных тел. – М.: Наука, 1983. – 336 с.
5. Прокопович И.Е., Зедгенидзе В.А. Прикладная теория ползучести.–М.: Стройиздат, 1980.– 240 с.
6. Гольшев А.Б., Ткаченко И.Н. Практические способы учета ползучести и усадки бетона при расчете железобетонных конструкций. – К.: Логос, 2000.– 87 с.
7. Рекомендации по учету ползучести и усадки бетона при расчете железобетонных конструкций /НИИЖБ. – М.: Стройиздат, 1988. – 121 с.
[1] Примеры несиловых воздействий: нагрев или охлаждение (иначе – температурные воздействия), высушивание или увлажнение (влажностные воздействия), перемещения опор, погрешности изготовления и монтажа; соответствующие деформации – температурное расширение, усадка или набухание, деформации от заданных перемещений; все они иногда называются вынужденными деформациями. При отсутствии связей, препятствующих деформированию тела, его деформации от несиловых воздействий называются свободными, а при наличии таких связей – связанными.
Дата добавления: 2021-12-14; просмотров: 117;










