Лекция 2. Расчет стержневых систем по стадии предельного равновесия

Методы расчета конструкций на стадии предельного равновесия чаще всего гораздо проще и, что еще важнее, экономичнее расчета по упругой стадии. Они позволяют получить предельную нагрузку, не выполняя громоздкого и трудоемкого расчета конструкции как физически нелинейной системы. Экономичность рассматриваемых методов расчета обусловлена тем, что они позволяют получить несущую способность конструкции, то есть, нагрузку в момент исчерпания прочности всех лишних связей. В этот момент система перестает быть геометрически неизменяемой и превращается в механизм (но с заданными обобщенными усилиями в заданных сечениях). Простота этих методов обеспечивается тем, что при определенных условиях (прежде всего, при простом пропорциональном загружении) предельное состояние не зависит от предшествующих состояний. Так как в предельном состоянии наиболее существенную роль играют пластические деформации, методы расчета конструкций по стадии предельного равновесия основаны на результатах теории пластичности, а именно - на двух ее теоремах, статической и кинематической.

Нам для дальнейшего необходимо ввести следующие понятия:

1) статически возможными называются распределения напряжений, удовлетворяющие уравнениям равновесия и заданным нагрузкам;

2) безопасное статически возможное напряженное состояние - это такое статически возможное состояние, при котором условие текучести еще нигде не достигнуто;

3) статически допустимое напряженное состояние отличается от безопасного статически возможного тем, что в некоторых зонах конструкции (сечениях, точках) условие текучести достигнуто (выход за пределы области текучести пространства напряжений вообще физически невозможен, т.к. материал не может находится в таком состоянии);

4) деформации (скорости деформаций) называются кинематически возможными, если они рассчитаны по перемещениям, отвечающим связям (прежде всего - опорным закреплениям конструкции);

5) поле перемещений (деформаций) или их скоростей в состоянии предельного равновесия называется механизмом разрушения.

Статическая теорема может быть сформулирована следующим образом:

а) тело может выдержать внешние нагрузки, если на каждом этапе загружения может быть найдено безопасное статически возможное напряженное состояние;

б) тело не может выдержать внешние нагрузки, для которых не существует статически допустимого распределения напряжений.

Таким образом, нижняя оценка несущей способности (предельной нагрузки) - это нагрузка, вызывающая статически допустимое распределение напряжений.

Кинематическая теорема:

а) тело не может выдержать заданную нагрузку, если существует поле кинематически возможных перемещений (скорость перемещений, деформаций, скоростей деформаций), для которого работа заданных внешних нагрузок (скорость этой работы) превышает пластическую диссипацию энергии в теле: , для идеально-пластического тела

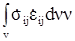
б) тело может выдержать внешние нагрузки, если для всех кинематически возможных полей деформаций (скоростей деформаций) выполняется условие, обратное условию а) настоящей теоремы.

Таким образом, кинематическая теорема дает верхнюю оценку предельной нагрузки как такой нагрузки, при которой для любых кинематически возможных (то есть, соответствующие опорным закреплениям) перемещений (или их скоростей) справедливо условие, обратное условию а) настоящей теоремы.

Разумеется, пользоваться нижней оценкой несущей способности более безопасно; однако, расчет на основе статической теоремы более сложен и для нетривиальных случаев требует применения специальных численных методов (поиска экстремума, или оптимизации) и использования ЭВМ. В то же время, сложность и трудоемкость расчета на основе кинематической теоремы могут быть существенно уменьшены, если, как это почти всегда бывает, удается на основе эмпирических данных или интуитивно априори наметить схему разрушения системы.

Более значительное упрощение в решении задач предельного анализа можно получить, если для описания физических зависимостей вместо более адекватной модели упругопластического тела (в случае одноосного деформирования она описывается диаграммой Прандтля) применить ее более простой предельный вариант - модель жестко-пластического тела (в случае одноосного деформирования Е=¥, напряжения определены только при e ³ e_т и равны s_т).

Но самое большое упрощение дает применение модели жестко-пластического тела в сочетании со схемой сосредоточенных деформаций, где деформации, распределенные по объему тела, считаются сосредоточенными в одном или нескольких сечениях. Для стержневого элемента это дает предельное значение момента М* = s_тW_pl; для прямоугольного сечения и симметричной диаграммы (s*_t = s_т, s*_с = - s_т) согласно формулы (2) лекции 1

W_pl = 1,5 W

Анализ следствий из статической теоремы показывает, что если некоторые лишние связи оказываются перешедшими в пластическое состояние на каком-то этапе загружения, то при дальнейшем увеличении нагрузки возможно установление статически допустимого распределения напряжений, то есть, конструкция эти увеличенные нагрузки сможет выдержать; при этом возможны различные сочетания реакций перешедших в пластическое состояние связей, удовлетворяющие заданным нагрузкам. Это приводит к методу пластического перераспределение усилий.

В приложении к расчету многопролетных балок (рис.1) этот метод выглядит следующим образом. Лишними связями считаем связи, обеспечивающие совместность поворотов смежных сечений сопрягаемых на промежуточной опоре пролетов, то есть, обеспечивающие работу неразрезной балки над примыкающим шарниром; их реакциями (лишними неизвестными) являются опорные моменты. Тогда эти большие по модулю опорные моменты, достигшие предельной величины раньше, можно в процессе загружения “заморозить” на этом уровне, благодаря чему меньшие опорные моменты будут после этого расти быстрее, вплоть до достижения своего предельного значения, и т.д., до тех пор, пока нагрузка на балку не достигнет предельного уровня, соответствующего несущей способности балки. При этом предельные значения моментов задаются конструктором при конструировании балки, и имеется возможность “выравнивания” опорных моментов, то есть, уменьшения или ликвидации разности между наибольшим и наименьшим по модулю значениями опорных и пролетных моментов, что может благоприятно сказаться на расходе материалов или сложности конструкции балки. Этот результат может быть получен наложением на эпюру изгибающих моментов, полученных расчетом по упругой стадии работы, треугольных (в пределах каждого пролета) эпюр “выравнивающих” моментов (рис.1,б), “исправляющих” эту “упругую” эпюру путем “выравнивая”. Можно вписать эпюры изгибающих “балочных” моментов в “эпюру материалов”, то есть, между эпюрами предельных положительных и отрицательных моментов, задаваемых при конструировании балки назначением сечений таким образом, чтобы удовлетворить тем или иным требованиям - критериям оптимальности (минимума массы, минимума трудоемкости и т.д.). Можно подобрать “выравнивающие” моменты по критерию максимума несущей способности.

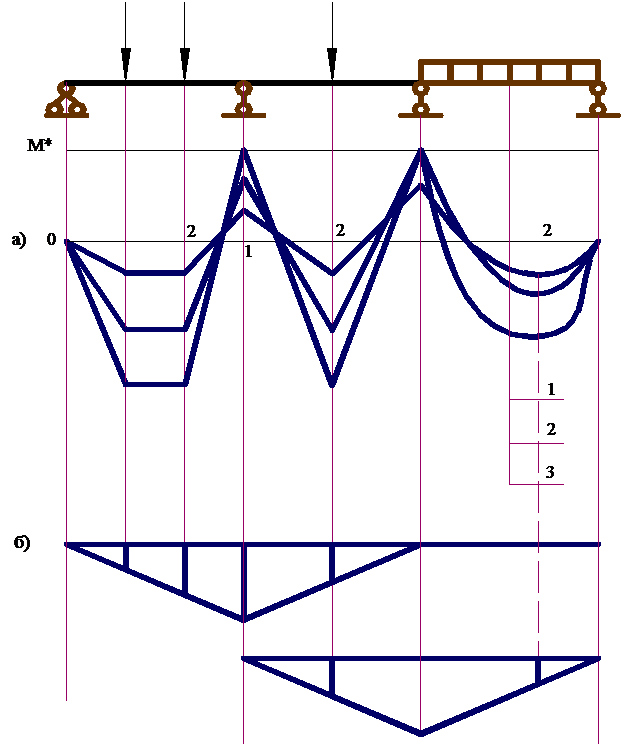
Рис. 1. Многопролетная балка

а – эпюры изгибающих моментов на различных стадиях загружения с учетом перераспределения;

б – эпюры «выравнивающих» моментов

Рассмотрим применение методов предельного анализа (анализа конструкции в состоянии предельного равновесия) с целью определения несущей способности на примере однопролетной балки, загруженной равномерно распределенной нагрузкой q, защемленной на левой и шарнирно опертой на правой опоре (рис.2, а). Вначале применим статическую теорему. Напряженное состояние балки будем характеризовать неизвестным В - опорной реакцией правой (шарнирной) опоры. Балка один раз статически неопределима, поэтому для превращения в механизм нужен переход в пластическую стадию двух связей (рис.2, б); для балок обычно это связи, обеспечивающие совместность поворотов смежных сечений в местах максимальных по модулю моментов, то есть, в опорном 1 и неизвестном пролетном 2 сечениях с абсциссой

. Условия равновесия этих сечений:

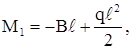(2.1)

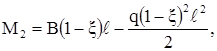(2.2)

Условия текучести

|M₁| = M*, (2.3)

M₂ = M*, (2.4)

Кроме того, в месте максимального момента

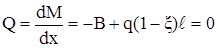(2.5)

Из условий (1)...(4) следует

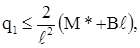(2.6)

(2.7)

откуда, область статически допустимых значений нагрузки q выглядит, как показано на рис. 3, где она заштрихована. Наибольшему значению нагрузки соответствует значение реакции В, определяемое уравнением q₁ = q₂:

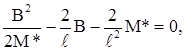(2.8)

откуда

(2.9)

что совместно с (5) позволяет определить положение пролетного пластического шарнира

2. Пример расчета. Исходные данные и механизм разрушения

а – расчетная схема

б – пластические шарниры

в – перемещения на стадии предельного равновесия

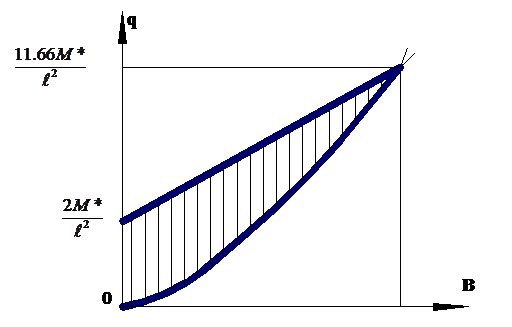Рис. 3. Пример расчета. Область статически допустимых значений нагрузки для рассчитываемой балки

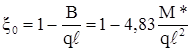(2.10)

Несущая способность:

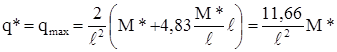(2.11)

В более сложных случаях предельное напряженное состояние можно определить только приближенно и ему будет соответствовать предельная нагрузка, определенная с запасом.

Применение кинематической теоремы заключается в отыскании механизма разрушения (“точного” или приближенного) и соответствующей нагрузки, оценивающей несущую способность сверху. Как уже упоминалось, во многих случаях механизм разрушения может быть принят априори. Зададим для рассматриваемой балки механизм разрушения двумя пластическими шарнирами: одним заданным - у опоры и одним искомым -в пролете с неизвестной координатой 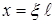, уровень перемещений можно задавать параметром f - прогибом в сечении 2. Исходя из модели жесткопластического тела, считаем, что линия прогибов балки имеет вид, показанный на рис.2,в. Тогда работа внешней нагрузки q:

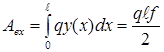(2.12)

Пластическая диссипация энергии в материале жесткопластической балки сосредоточена в сечениях пластических шарниров и равна работе напряжений в сечении на сосредоточенных пластических деформациях DU:

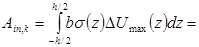
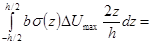
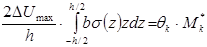(2.13)

где k - номер пластического шарнира;

q_к - угол излома оси балки в k-ом пластическом шарнире;

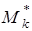- предельный момент в k-ом пластическом шарнире.

Таким образом, согласно кинематической теоремы (А_eх £ А_in):

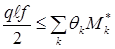(2.14)

Из рис.36.4в видно, что q₁ = q₂= 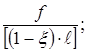следовательно,

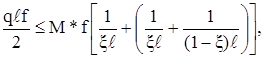(2.15)

откуда

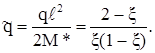
Так как 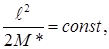экстремумы q и 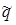достигаются в одном сечении x₀, определяемом из уравнения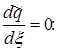

=0 (2.17)

Эта функция обращается в нуль при

.

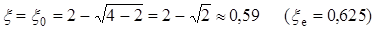Подставляя это значение x в (16), получим

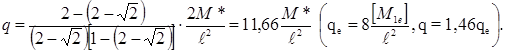(2.18)

Это верхняя оценка несущей способности.

Таким образом, в нашем тривиальном случае нижняя и верхняя оценки несущей способности совпадают и дают ее “точное” (в рамках рассматриваемой модели) значение.

Если бы мы получили значение x₀ из эксперимента или приняли его интуитивно, можно было бы подставить его сразу в (2.15), откуда получить то же значение q.

Для однопролетной балки с обеими защемленными опорами можно из соображений симметрии принять x = 0,5,

,

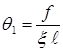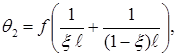
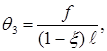
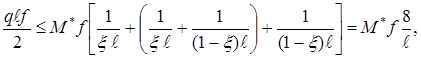(2.19)

откуда

(2.20)

Таким образом, чтобы получить несущую способность системы, необходимо:

а) в случае применения статической теоремы - задать множество статически допустимых состояний, характеризующихся статическими параметрами (реакциями опор, усилиями в сечениях и т.д.), и найти такие значения этих параметров, при которых конструкция выдерживает максимальную нагрузку; эта нагрузка и будет оценкой несущей способности снизу (тем лучшей, чем более полно заданное множество статически допустимых состояний);

б) в случае применения кинематической теоремы - задать множество кинематически возможных полей перемещений, характеризующихся кинематическими параметрами (например, координатой пластического шарнира, места сосредоточенного растяжения и т.д.), и найти такие значения этих параметров, при которых конструкция выдерживает минимальную нагрузку; эти нагрузки и будут оценкой несущей способности сверху (см. замечание о полноте множества состояний, из которых отбирается искомое).

В реальных гораздо более сложных случаях (как правило, при применении статической теоремы, а также при применении кинематической теоремы, если наметить механизм разрушения априори не удается) приходится применять мощные методы линейного или, в отдельных случаях, нелинейного программирования.

Часто механизм разрушения может быть установлен заранее, и тогда несущая способность определяется из решения уравнения баланса работы (или мощности) внешних сил и диссипации (скорости диссипации) внутренних сил.

При расчете рам и арок следует иметь ввиду, что в них, в общем случае, напряженное состояние сечения определяется несколькими обобщенными силами - в плоском случае тремя (N, M, Q), в пространственном - шестью (N, M_x, M_y, M_xy, Q_x, Q_y), а сосредоточенные обобщенные деформации - соответствующими тремя (DU, Dq, DV) или шестью (DU, Dq_x, Dq_y, Dq_xy, DV_x, DV_y) параметрами.

Кроме того, необходимо помнить, что на стадии предельного равновесия конструкция весьма деформативна, в особенности - из-за наличия пластических шарниров и других мест сосредоточенных деформаций. Так как нормы ограничивают перемещения конструкций, это создает соответствующую проблему их контроля (а также, для железобетонных конструкций, - контроля их трещиностойкости. Однако, эти вопросы выходят за рамки нашей лекции.