Непрерывные случайные величины: нормальный закон распределения.

Определение. Непрерывная случайная величина x называется распределённой по нормальному закону Гаусса, если её плотность распределения 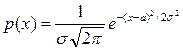, где s>0.

Таким образом, значения а и s полностью определяют функцию р(х).

Для упрощения записи функции p(x) введём функцию 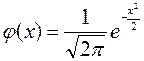. Это чётная и неотрицательная функция. Её график приведён на рисунке ниже.

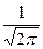
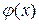
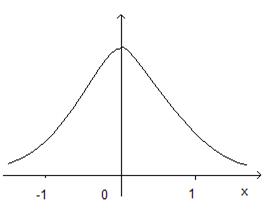
Тогда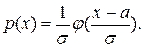

График плотности распределения нормальной случайной величины при 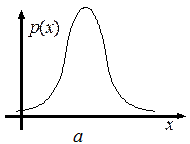некоторых значениях а и s представлен на другом рисунке. График симметричен относительно прямой х = а, и выполняются условия: р(х) ® 0 при х ® ±µ. Если а увеличивать, оставляя s неизменной, то график будет перемещаться вправо, а если а уменьшать, то влево, не изменяя формы.

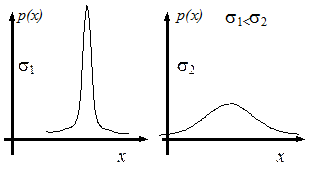Если значение а неизменно, то относительно малому значению s будет соответствовать график р(х) с выраженным пиком, как на левом рисунке. При относительно большом значении s график р(х) представляет собой пологую кривую, как изображено на правом рисунке.

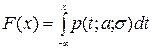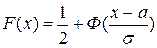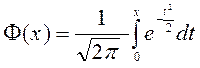Функция распределения F(x) нормальной случайной величины x выводится обычным способом по формуле: . Доказательство опускаем, , где — знаменитая интегральная функция Лапласа. Она нечётная и значения её табулированы.

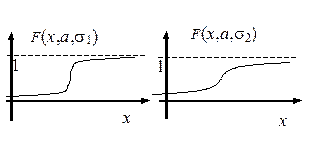Графики функций F(x) для нормально распределённых случайных величин при различных значениях s
изображены на рисунках, s₁<s₂.

Аналогично предыдущему вычисляются Mx и Dx. Выпишем без доказательства: Mx = a ^.и Dx = s².

Таким образом, параметры а и s в формуле для плотности распределения случайной величины, распределённой по нормальному закону, приобретают смысл: а – математическое ожидание, s² – дисперсия.

Вероятность того, что нормально распределённая случайная величина x примет значение из промежутка (х₁, х₂) рассчитывается по формуле

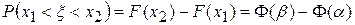, где 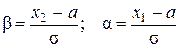. Значения F(х) определяются из таблицы Лапласа.

Если случайная величина x имеет плотность распределения, выражающуюся функцией p(x;0;1), то есть x – нормально распределённая случайная величина с математическим ожиданием, равным нулю, и дисперсией, равной единице, тогда .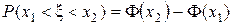

Случайную величину с плотностью распределения p(x;0;1) можно принять за некоторый эталон для случайных величин, распределённых по нормальному закону. График плотности распределения такой случайной величины симметричен относительно оси ординат.