Принципы организации и способы представления данных в ГИС
Хранение данных в ГИС организуют в соответствии со следующими принципами:
1) использование данных оптимально как одним, так и несколькими приложениями;
2) данные независимы от программ, использующих эти данные;
3) для операций с данными применяют общий управляющий способ;
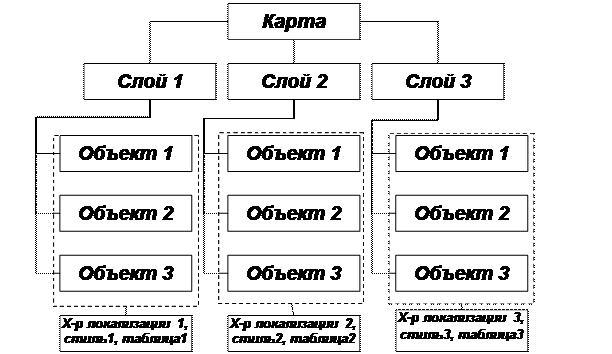
Рис. 3.1. Структура картографической информации
4) структура данных позволяет модернизировать и расширять функциональные возможности приложений.
В практике ГИС достаточно давно определился набор базовых способов представления (базовых моделей) пространственных данных, используемых для описания планиметрических (двумерных или меньшей размерности) объектов:
1) растровая модель;
4) векторная модель:
- векторная топологическая (линейно-узловая) модель;
- векторная нетопологическая модель (модель «спагетти»).
Растровая модель данныхподразумевает разбиение пространства (координатной плоскости) на дискретные элементы, упорядоченные в виде прямоугольной матрицы (рис. 3.2.). Исходные полигональные объекты рис. 3.2(а) с атрибутами (классами) А, В, С, D, E и матрица размером 7´7(рис. 3.2(б) растровой модели, каждому элементу которой присвоено значение атрибута объекта.
Положение точечного объекта определяется номерами столбца и строки матрицы (при необходимости координаты любого угла ячейки или ее центра могут быть вычислены). Ячейке (пикселу) присваивается цифровое значение, определяющее имя или семантику (атрибут) объекта.
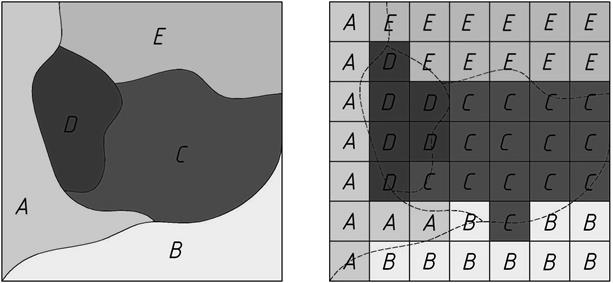
| а Исходная карта контуров | б Представление карты с использованием ячеек матрицы |
Рис. 3.2. Растровая модель данных
Выбирая подходящий размер пикселов, можно добиться пространственного разрешения, удовлетворяющего целям их цифрового описания и последующей обработки, но при этом увеличивается необходимый для работы объем памяти (при двукратном увеличении разрешения объем хранимых данных увеличивается в четверо). Удобство матричной модели состоит в том, что к данным, организованным подобным образом, легко применяются алгоритмы матричной алгебры, математический аппарат которой относительно прост и хорошо разработан. Недостаток – значительные затраты машинной памяти, требуемой для хранения данных.
Векторные модели данныхвключает векторные топологические и векторные нетопологические модели.
Векторная топологическая (линейно-узловая) модель – представление линейных и полигональных пространственных объектов, описывающее как геометрию, так и топологические отношения (связи) между полигонами, дугами и узлами. Линейно-узловое представление можно проиллюстрировать следующей схемой (Рис.3.6). Все точки, которые определяют положение объектов в пространстве (независимо от того, каким объектам они принадлежат), собраны в один список («глобальный список точек»), а все линии, из которых состоят объекты F1 и F2 карты собраны в «глобальный список линий». Каждый объект содержит в своей структуре данных только на описатели линий (ребер), из которых состоит полигон. Каждая структура, описывающая линию, содержит не координаты точек, а указатели на те точки из «глобального списка точек», которые являются ее концами.
Недостаток линейно-узлового представления – усложнена процедура изменения формы объектов, так как одна точка фактически может принадлежать сразу двум полигонам, и изменение ее координат приведет к изменению формы смежных объектов.
Векторная нетопологическая модель (модель «спагетти») – представление пространственных объектов с описанием только их геометрии в виде неупорядоченного набора дуг (сегментов).
Внутренняя структура данных в модели «спагетти» для фрагмента карты, состоящего из двух полигонов, представлена на рис. 3.7. В этом случае 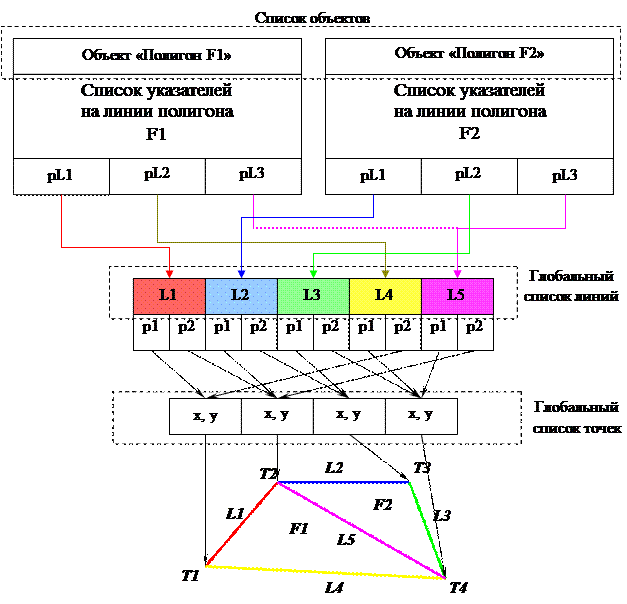
Рис. 3.6. Описание объектов в линейно-узловой модели
каждый объект содержит в своей структуре данных координаты всех своих вершин.
Недостаток векторной нетопологической модели – некоторая избыточность данных, так как координаты общих для полигонов точек Т2 и Т4 хранятся в двух местах – структуре данных полигона F1 и структуре данных полигона F2.
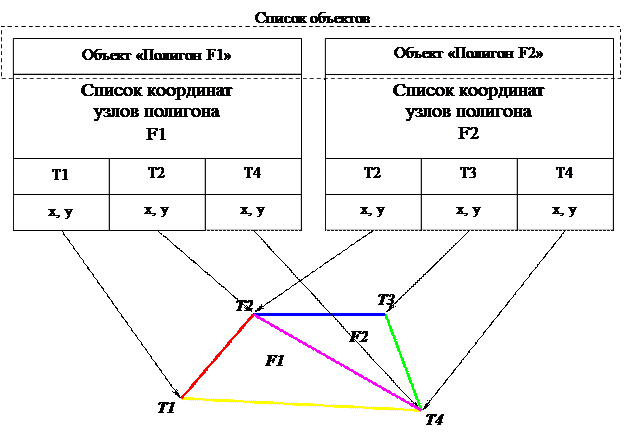
Рис. 3.7. Описание объектов векторной нетопологической (спагетти) модели
Дата добавления: 2018-05-10; просмотров: 2450;











