Схема делителя с исключением начальных состояний.

В основе такого делителя лежит асинхронный суммирующий счётчик на JK триггерах с инверсными установочными RS входами. Минимальное количество триггеров в счётчике должно удовлетворять требованию:

2^n-1<K<2ⁿ.

Так, если необходимо построить счётчик с коэффициентами пересчёта К_СЧ= 10 следовательно n=4. Наибольший коэффициент счёта в данной схеме К_СЧнаиб = 16. Тогда для нашего случая лишними являются 6 состояний: от 0 до 5.

В данной схеме, кроме счётчика, в качестве дешифрирующего устройства используется элемент «И-НЕ».

Исходным состоянием при работе данного делителя является 6₁₀=0110₂. По мере поступления счётных импульсов на вход номер состояний счётчика изменяется от 6 до 16. Затем, очередной импульс переводит счётчик в 0, а на вход элемента «И-НЕ» DD1 поступает 1. 0 с выхода DD1 через инверсные входы S триггеров второго и третьего разрядов устанавливает эти разряды в 1 (в исходное состояние). Так, в конце цикла счёта в счётчике сразу же обеспечивается ненулевое начальное состояние 6₁₀=0110₂. Далее работа повторяется.

Таким образом, нулевое состояние разрядов является промежуточным. Оно существует в течении короткого времени и используется в качестве признака для выработки сигнала обратной связи.

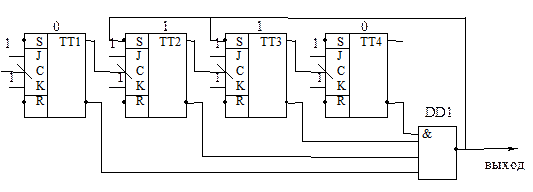
Рис. 12

ВЫВОД: В делителе с постоянными коэффициентами деления коэффициент пересчёта задан жёстко на схемном уровне.

Делители с переменными коэффициентами деления.

Счётчики с коэффициентом счёта К_СЧ=2ⁿ могут быть использованы для построения пересчётных схем с переменным коэффициентом пересчёта К_СЧ<2ⁿ - делителей с переменным коэффициентом деления (ДПКД).

ДПКД позволяет получить коэффициент деления через 1. Например, 3-х разрядный ДПКД позволяет получить коэффициент деления от 1 до 999. Рассмотрим работу такого делителя, учитывая, что коэффициент деления равен 537.

Делитель строится на базе трёх декадных счётчиков и дополнительных элементов умножения. В этом счётчике есть выход, на котором появляется 1, когда счётчик перейдёт в состояние 10.

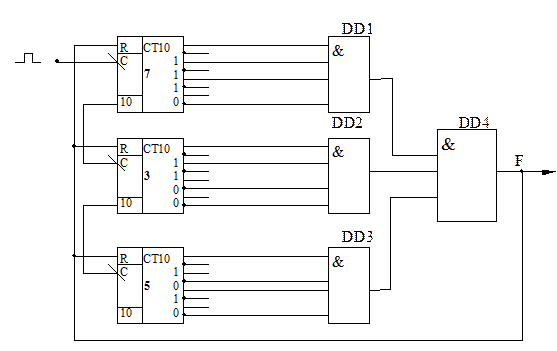
Рис. 13

Работа.

Делитель имеет три декады:

1. Декада единиц – переключается каждым импульсом.

2. Декада десятков – переключается каждым десятым импульсом.

3. Декада сотен – переключается каждым сотым импульсом.

Элементы DD1, DD2, DD3, DD4 играют роль дешифратора.

Так, например для нашего случая, на выходе DD1 будут 1 только тогда, когда первая декада установит цифру 7 (цифру 1 заданного коэффициента деления). Элемент DD2 выдаст 1 только тогда, когда на его входах будет тройка (число, соответствующее десятичным заданным коэффициентам деления). Элемент DD3 устанавливает единицу, когда на выходе третьей декады будет 5, т.е. число, соответствующее сотням коэффициента деления. Затем 1 с элементов DD1, DD3 умноженным элементом DD4 и на выходе подаётся 1, один раз на 537 импульсов (К_ДЕЛ). Эта 1 обнуляет все декадные счётчики.

В аппаратуре связи и управления коэффициенты деления задаются с помощью десятичных позиционных переключателей. Эти переключатели осуществляют коммутацию элементов DD1-DD3.

В современной аппаратуре используется делителей с переменным дробным коэффициентом деления ДДПКД. Дробный коэффициент пересчёта достигается за счёт использования декад долей 1-ц, 10-ов, 100-н и т.д. Кроме того, в процессе работы осуществляется усреднение целочисленных коэффициентов деления путём периодического использования то К_ДЕЛ, то К_ДЕЛ+1.

ВЫВОД: В делителе с переменным коэффициентом деления коэффициент пересчёта не задан жёстко на схемном уровне.

Заключение:

1. Делитель – это счётчик, информация с которого снимается со старшего разряда и который обнуляется после поступления на него заданного числа импульсов.

2. Наиболее широко применяется делитель с переменно-дробным коэффициентом деления.

3. В основе счётчика лежит простейший Т-триггер.

4. Счёт в счётчиках осуществляется последовательно.