Третий тип задач - пересечение поверхностей общего положения
ПЕРЕСЕЧЕНИЕ КРИВЫХ ПОВЕРХНОСТЕЙ
Задача второго типа - одна из поверхностей имеет вырожденный вид
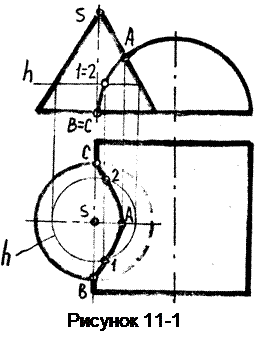Пример 1. Построить линию пересечения полуцилиндра конусом вращения (рисунок 11-1).
На виде спереди линия пересечения уже имеется - она совпадает с вырожденным видом полуцилиндра и находится в пределах площади наложения обеих поверхностей.
Способом принадлежности построим точки линии пересечения на виде сверху. Сначала определим опорные точки, к которым относятся ближняя и дальняя, верхняя и нижняя, левая и правая, а также точки видимости. Опорными в данном случае являются точки: А- верхняя и правая, В- нижняя и ближняя, С- нижняя и дальняя.
Для построения случайных точек линии пересечения воспользуемся параллелями (горизонталями) поверхности конуса, которые на виде сверху проецируются без искажения в окружности. На чертеже проведена параллель h, с помощью которой найдены точки 1 и 2.
Третий тип задач - пересечение поверхностей общего положения
Этот тип задач является наиболее сложным.
Общим способом построения линии пересечения в этом случае является способ поверхностей-посредников. В качестве поверхностей-посредников используют плоскости общего или частного положения и сферы. Мы не будем рассматривать применение плоскостей общего положения, поскольку на практике чаще используют плоскости-посредники частного положения.
Способ плоскостей-посредников применяют в тех случаях, когда обе поверхности можно пересечь по графически простым линиям. Эти линии на одном из видов будут обязательно совпадать и поэтому такой способ можно трактовать как способ конкурирующих линий.
Под графически простыми линиями следует понимать две линии - прямую и окружность, построение которых не вызывает затруднений.
При построении линии пересечения всегда следует соблюдать определенную последовательность: в первую очередь строят опорные точки, которые позволяют видеть в каких пределах расположены проекции линии пересечения, и где имеет смысл определять случайные точки.
Построение точек линии пересечения поверхностей указанным способом состоит в проведении проецирующих плоскостей, пересекающих обе данные поверхности по графически простым линиям (прямым или окружностям). Пересечение этих линий, принадлежащих разным поверхностям и лежащим в одной секущей плоскости, определяет точки общие для обеих поверхностей – точки принадлежащие линии их пересечения.
Следовательно, если у пересекающихся поверхностей имеются семейства графически простых линий, лежащих в проецирующих секущих плоскостях (или конкурирующих друг с другом), то точки пересечения этих линий и будут точками искомой линии пересечения.
Рассмотрим несколько примеров построения линии пересечения поверхностей указанным способом.
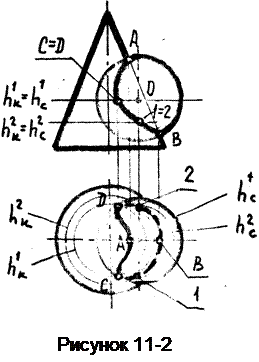
Пример 2. Построить линию пересечения конуса вращения со сферой (рисунок 11-2).
В качестве посредника здесь следует взять горизонтальную плоскость (или фронтально-конкурирующие параллели hк и hс, которые представляют собой окружности).
Сначала определим опорные точки. Точки А и В, находящиеся в месте пересечения контурных линий конуса и сферы, будут соответственно высшей и низшей, и одновременно точками видимости для вида спереди (т.к. обе поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций).
Для определения точек видимости на виде сверху, возьмем на виде спереди пару конкурирующих линий h'к=h'с, расположенных на уровне экватора сферы. Построив эти линии на виде сверху, находим точки С и D, которые и будут точками видимости этого вида.
Для определения случайных точек берем пару фронтально-конкурирующих линий h²к=h²с. Построив их на виде сверху, находим на пересечении этих линий точки 1 и 2, которые затем отмечаем на виде спереди.
Подобным образом находим и остальные случайные точки линии пересечения, которые затем соединяем плавной кривой; с учетом её видимости.
Пример 3.Построить линию пересечения конуса вращения и цилиндра вращения, оси которых скрещиваются (рисунок 11-3).
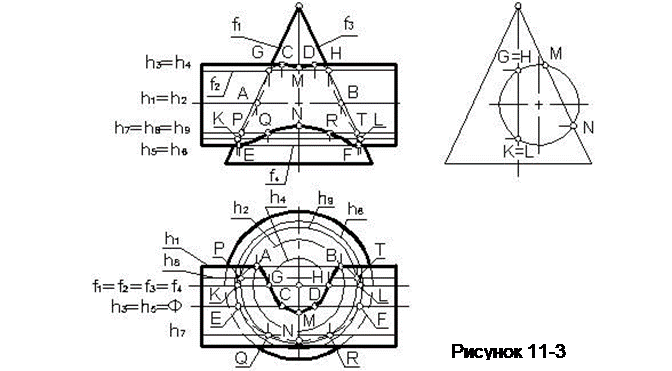
Если пересекать обе поверхности горизонтальными плоскостями, то на поверхности цилиндра появятся образующие (прямые линии), а на конусе – его параллели (окружности). На виде спереди (фронтальной проекции) эти линии будут конкурировать; на виде сверху (горизонтальной проекции) окружности (параллели конуса) будут изображаться без искажений.
Для начала определим опорные точки. На виде сверху (горизонтальной проекции) для цилиндра точками видимости являются точки А и В, которые одновременно будут и самыми дальними точками линии пересечения. Эти точки находятся на пересечении контурной образующей цилиндра h1 и конкурирующей с ней параллелью конуса h2. У конуса точек видимости на виде сверху нет, поскольку вся его поверхность здесь видима. На виде спереди (фронтальной проекции) точки видимости для цилиндра C,D и E,F находятся на пересечении контурных образующих цилиндра h3и h5 и конкурирующих с ними параллелей конуса h4 и h6. При этом точки C и D будут высшими точками линии пересечения, а точки E и F– низшими. Для конической поверхности здесь точками видимости будут точки G,H и K,L, находящиеся на пересечении контурных образующих конуса f1 и f3 и конкурирующих с ними образующих цилиндра f2 и f4. При этом фронтальные проекции образующих f2 и f4 построены с помощью вида слева (профильной проекции).
Точки M и N найдены на пересечении контурной образующей конуса p с окружностью, в которую «вырождается» поверхность цилиндра на виде слева.
После нахождения опорных точек можно построить несколько случайных, например P,Q,R и T, уточняющих линию пересечения поверхностей. Эти точки находятся на пересечении образующих цилиндра h7и h8 и конкурирующей с ними параллели конуса h9.
Построив аналогично достаточное количество случайных точек, соединим их в определенной последовательности, учитывая условия видимости. В нашем примере видимость проекций линии пересечения определяется цилиндрической поверхностью. Поэтому видимыми будут только те ее участки, которые расположены на видимой части цилиндрической поверхности.
Дата добавления: 2017-11-21; просмотров: 4067;
Поиск по сайту
Узнать еще
- D-технология построения чертежа. Типовые объемные тела: призма, цилиндр, конус, сфера, тор, клин. Построение тел выдавливанием и вращением. Разрезы, сечения.
- I. Демократия как тип политического режима.
- I. ОСНОВНЫЕ ПОЛОЖЕНИЯ
- I. Политический режим: понятие, сущность и основные типы.
- I. Понятие и типы политических партий.
- I. Решение логических задач средствами алгебры логики
- I.2.5 ТРЕТИЙ ЗАКОН НЬЮТОНА
- IDL-описаниеи библиотека типа
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
