Частота, при которой ЛАЧХ пересекает ось частот носит название частоты среза.

ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси 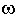. Величина 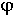( 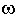) откладывается по оси ординат в градусах или радианах. Для элементарных звеньев она не выходит за пределы: - + .

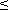
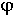
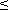ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.

При исследовании и проектировании САУ часто используют АФЧХ, ЛАЧХ и ЛФЧХ разомкнутых систем. Это объясняется тем, что разомкнутые САУ более просто исследовать экспериментально, чем замкнутые. В то же время по ним можно получить исчерпывающую информацию о поведении данной САУ в замкнутом состоянии.

Любую многоконтурную САУ можно привести к одноконтурной. Разомкнутая одноконтурная САУ состоит из цепочки последовательно соединенных динамических звеньев. Зная передаточную функцию разомкнутой САУ можно построить ее ЧХ. И наоборот, зная ЧХ разомкнутой САУ, снятую, например, опытным путем, можно найти ее передаточную функцию.

Передаточная функция разомкнутой одноконтурной системы равна произведению передаточных функций отдельных звеньев:

.

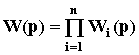Заменив в этом выражении p на j w получим ее АФЧХ:

.

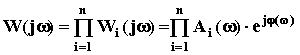АЧХ: ,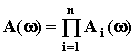

значит ЛАЧХ равна сумме ЛАЧХ звеньев: .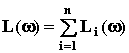

ЛФЧХ: .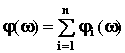

Таким образом ЛАЧХ и ЛФЧХ разомкнутой САУ строят путем графического сложения ЛАЧХ и ЛФЧХ звеньев. При этом ограничиваются построением асимптотической ЛАЧХ.

Для построения ЛАЧХ и ЛФЧХ рекомендуется следующий порядок:

1) раскладывают сложную передаточную функцию на множители, являющиеся передаточными функциями типовых динамических звеньев (порядок полиномов числителя и знаменателя не выше второго);

2) вычисляют сопрягающие частоты отдельных звеньев и строят асимптотические ЛАЧХ и ЛФЧХ каждого элементарного звена;

3) путем графического суммирования ЛАЧХ и ЛФЧХ звеньев строят результирующие ЧХ.

Рассмотрим конкретный пример:

W(p) = 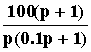= W₁W₂W₃W₄.

Раскладываем данную передаточную функцию на передаточные функции элементарных звеньев:

1) безынерционное звено:

W₁ = K₁ = 100 => L(w) = 20lg100 = 40;

2) форсирующее звено:

W₂ = p + 1;

его параметры:

K₂ = 1, T₂ = 1, ₂ = 1/T₂ = 1;

3) интегрирующее звено:

W₃ = 1/p;

его ЛАЧХ проходит через точку L = 0 при частоте = 1;

4) апериодическое звено:

W₄ = 1/(0.1p + 1);

его параметры: K₄ = 1, T₄ = 0.1, ₄ = 1/T4 = 10.

Порядок построения ЛАЧХ и ЛФЧХ показан 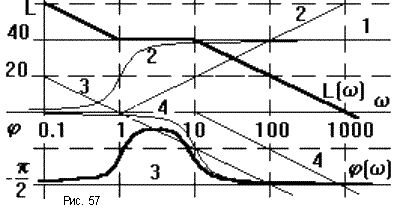на рис.57.

Иногда требуется решить обратную задачу, то есть определить передаточную функцию по известной ЛАЧХ. Процедура определения передаточной функции состоит из следующих этапов:

1) известная ЛАЧХ представляется в асимптотическом виде, для этого непрерывная кривая заменяется отрезками прямых либо горизонтальных, либо с наклоном, кратным ±20 дб/дек;

2) асимптотическая ЛАЧХ раскладывается на ЛАЧХ элементарных звеньев;

3) для каждой из полученных ЛАЧХ определяются k и 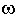₁ = 1/T и записывается передаточная функция типового звена;

4) передаточная функция САУ определяем путем перемножения передаточных функций типовых звеньев.

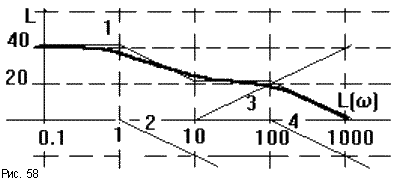
Описанный порядок иллюстрируется на рис.58.

Здесь ЛАЧХ может быть представлена суммой ЛАЧХ четырех типовых звеньев: пропорционального W₁ = 100, апериодического W₂ = 1/(p + 1), форсирующего W₃ = 0.1p + 1 и апериодического W₄ = 1/(0.01p + 1).

Таким образом, передаточная функция разомкнутой САУ имеет вид

.

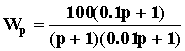В более сложных случаях наклоны ЛАЧХ на некоторых участках превышают ± 20дб/дек. Тогда помимо параметров K и T приходится определять еще и коэффициенты демпфирования r.

Зная передаточную функцию разомкнутой САУ можно построить ее уравнение динамики

=> => => .

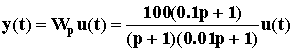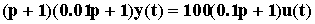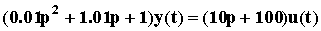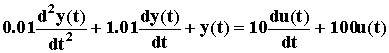Таким образом можно определить уравнение динамики реальных звеньев и всей реальной САУ, если оно теоретически это сделать затруднительно. Для снятия частотных характеристик реальной разомкнутой САУ на ее вход подают гармонический сигнал с изменяемой частотой и определяют изменение амплитуды и фазы выходного сигнала в зависимости от частоты. По полученным характеристикам определяют уравнение динамики, после чего САУ можно исследовать теоретически.