Линейные системы дифференциальных уравнений. Общая теория.
Линейной системой называют нормальную систему дифференциальных уравнений вида
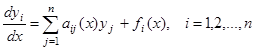 (4)
(4)
Если в формуле (4) все 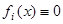 , то система называется однородной.
, то система называется однородной.
Также как и для линейного уравнения 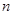 -го порядка можно показать, что условия теоремы Коши для системы (1), в которой все входящие в нее функции определены на интервале
-го порядка можно показать, что условия теоремы Коши для системы (1), в которой все входящие в нее функции определены на интервале 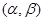 , сводятся к требованию непрерывности
, сводятся к требованию непрерывности 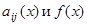 на этом интервале. При этом решение с начальными условиями
на этом интервале. При этом решение с начальными условиями 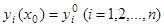 для произвольных
для произвольных 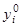 и
и 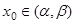 продолжаемо на весь интервал
продолжаемо на весь интервал 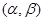 .
.
В дальнейшем, кроме обычных операций матричной алгебры, нам понадобятся операции дифференцирования и интегрирования матриц.
Производной от матрицы 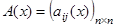 называется матрица
называется матрица 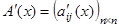 . Интеграл от матрицы определяется так:
. Интеграл от матрицы определяется так:
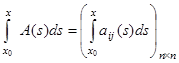 .
.
Используя матричные обозначения, запишем систему (4) в виде
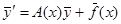 . (6)
. (6)
Начальные условия в матричной форме будут иметь вид (2/).
Однородная система
Пусть 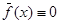 . Тогда получим однородную систему
. Тогда получим однородную систему
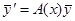 (7)
(7)
Пусть задано 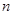 столбцов
столбцов
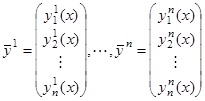 .
.
Составим из них матрицу
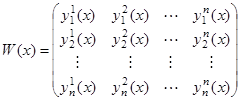 (8)
(8)
Наряду с уравнением (7), левая и правая часть которого суть вектор-столбцы, рассмотрим уравнение
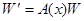 , (9)
, (9)
левая и правая часть которого – 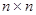 матрицы.
матрицы.
Теорема 1. Если 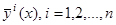 – решения уравнения (7), тогда матрица
– решения уравнения (7), тогда матрица 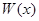 , определенная формулой (8), есть решение матричного уравнения (9). И обратно, если
, определенная формулой (8), есть решение матричного уравнения (9). И обратно, если 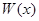 – решение матричного уравнения (9), то каждый столбец этой матрицы есть решение уравнения (7).
– решение матричного уравнения (9), то каждый столбец этой матрицы есть решение уравнения (7).
Для доказательства справедливости утверждения теоремы 1 достаточно расписать уравнение (9) поэлементно.
Столь же просто можно убедиться в справедливости следующего утверждения.
Теорема 2. Если 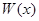 – решение уравнения (9), то
– решение уравнения (9), то 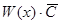 , где
, где 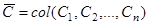 , будет решением уравнения (7), а
, будет решением уравнения (7), а 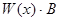 , где
, где 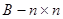 -матрица, также будет решением уравнения (9).
-матрица, также будет решением уравнения (9).
Определение. Будем говорить, что вектор-функции 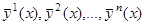 линейно зависимы на интервале
линейно зависимы на интервале 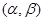 , если существуют постоянные
, если существуют постоянные 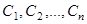 не все равные нулю такие, что
не все равные нулю такие, что
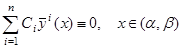 . (10)
. (10)
Если из соотношения (10) следует, что 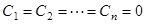 , то вектор-функции
, то вектор-функции 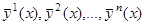 линейно независимы на
линейно независимы на 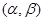 .
.
Пусть матрица 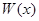 определена формулой (8),
определена формулой (8), 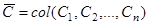 . Тогда соотношение (10) принимает вид
. Тогда соотношение (10) принимает вид
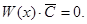 (10/)
(10/)
Определение. Функциональный определитель 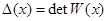 называют определителем Внонского (вронскианом) системы вектор-функций
называют определителем Внонского (вронскианом) системы вектор-функций 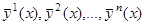 .
.
Теорема 3. Если решения 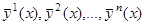 уравнения (7) линейно зависимы на интервале
уравнения (7) линейно зависимы на интервале 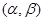 , то
, то 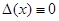 на
на 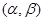 .
.
Доказательство. Если решения 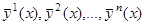 уравнения (7) линейно зависимы на интервале
уравнения (7) линейно зависимы на интервале 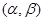 , то уравнение (10/), рассматриваемое как уравнение относительно неизвестного вектор-столбца
, то уравнение (10/), рассматриваемое как уравнение относительно неизвестного вектор-столбца 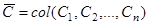 , имеет нетривиальное решение при любом
, имеет нетривиальное решение при любом 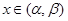 . Но тогда
. Но тогда 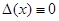 на
на 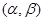 .
.
Замечание. Мы нигде не использовали тот факт, что 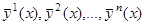 – решения уравнения (7). Таким образом , утверждение теоремы 2 справедливо для любых вектор-столбцов
– решения уравнения (7). Таким образом , утверждение теоремы 2 справедливо для любых вектор-столбцов 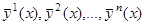 .
.
Теорема 4. Если 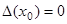 хотя бы для одного
хотя бы для одного 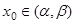 , где
, где 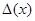 – определитель Вронского решений системы (7) с непрерывными коэффициентами, то эти решения линейно зависимы на
– определитель Вронского решений системы (7) с непрерывными коэффициентами, то эти решения линейно зависимы на 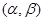 .
.
Доказательство. Пусть 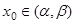 и
и 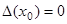 . Рассмотрим уравнение
. Рассмотрим уравнение 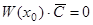 относительно
относительно 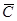 . Так как
. Так как 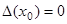 , то это уравнение имеет ненулевое решение
, то это уравнение имеет ненулевое решение 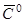 . Положим
. Положим 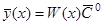 . Согласно теореме 2,
. Согласно теореме 2, 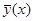 – решение линейной однородной системы (7). Но
– решение линейной однородной системы (7). Но 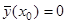 , поэтому, в силу теоремы единственности,
, поэтому, в силу теоремы единственности, 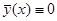 на интервале
на интервале 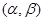 . Таким образом нам удалось найти такой нобор значений постоянных
. Таким образом нам удалось найти такой нобор значений постоянных 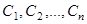 , что
, что 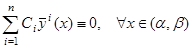 . Это и означает, что решения
. Это и означает, что решения 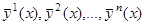 линейно зависимы.
линейно зависимы.
Следствие 1. Определитель Вронского системы решений 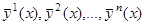 либо тождественно равен нулю на интервале
либо тождественно равен нулю на интервале 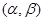 , и тогда решения линейно зависимы на этом интервале, либо он не обращается в ноль ни в одной точке интервала
, и тогда решения линейно зависимы на этом интервале, либо он не обращается в ноль ни в одной точке интервала 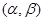 , и тогда решения линейно независимы на этом интервале.
, и тогда решения линейно независимы на этом интервале.
Определение. Фундаментальной системой решений однородной системы дифференциальных уравнений (7) называется любая система 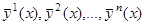 линейно независимых решений этой системы. Составленная из столбцов координат линейно независимых решений матрица (8) называется фундаментальной матрицей системы (7).
линейно независимых решений этой системы. Составленная из столбцов координат линейно независимых решений матрица (8) называется фундаментальной матрицей системы (7).
Отметим, что фундаментальная матрица может быть определена и по-другому на основании теоремы 4 и следствия из нее.
Определение. Фундаментальной матрицей системы (7) называется решение уравнения (9), не обращающееся в ноль ни водной точке интервала 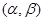 .
.
Теорема 5. Фундаментальная матрица системы (7) всегда существует.
Действительно, в силу следствия 1, в качестве фундаментальной матрицы можно взять решение системы (9) с начальным условием 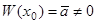 .
.
Теорема 6.Если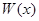 – фундаментальная матрица системы (7), то любое ее решение имеет вид
– фундаментальная матрица системы (7), то любое ее решение имеет вид 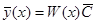 , где
, где 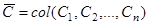 – постоянный столбец.
– постоянный столбец.
Доказательство. То, что 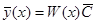 всегда является решением системы (7) уже доказано ранее. Пусть задано начальное условие
всегда является решением системы (7) уже доказано ранее. Пусть задано начальное условие 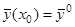 . Найдем значение постоянной
. Найдем значение постоянной 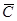 из условия
из условия 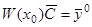 . Имеем:
. Имеем: 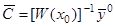 . Тогда
. Тогда 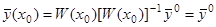 и в силу теоремы единственности найдено нужное решение.
и в силу теоремы единственности найдено нужное решение.
Найденное решение имеет вид
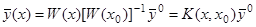 (11)
(11)
Матрица 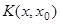 называется матрицантом системы (7). Она удовлетворяет условию
называется матрицантом системы (7). Она удовлетворяет условию 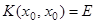 .
.
Дата добавления: 2022-05-27; просмотров: 155;











