Нормальные системы дифференциальных уравнений

Нормальной системой дифференциальных уравнений называется система в 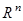вида

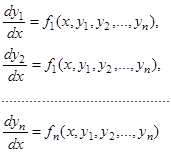(1)

Здесь 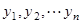– искомые функции, 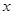– независимая переменная, 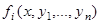– заданные функции.

Введя в рассмотрение векторы

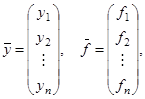
можем записать систему (1) в векторной форме

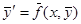. (1^/)

Задача Коши для системы (1) или (1^/) ставится следующим образом: найти решение системы, удовлетворяющее начальному условию

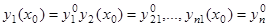(2)

или

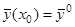(2^/)

Теорема(существование и единственности решения задачи Коши для нормальной системы). Пусть все функции 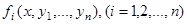непрерывны вмести со своими частными производными 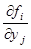в некоторой области 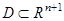, содержащей точку 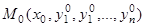. Тогда существует интервал 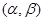и единственный набор дифференцируемых функций 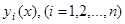, определенных на этом интервале, являющихся решением системы (1) на 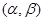и удовлетворяющих начальным условиям (2).

Общее решение системы (1) представляет собой совокупность 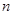функций 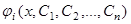таких, что 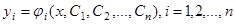– решение системы и при этом по начальному условию (2) можно указать единственный набор 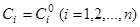такой, что .

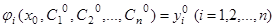Заметим, что любое уравнение 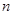-го порядка 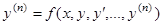может быть сведено к нормальной системе дифференциальных уравнений вида (1). Действительно, полагая 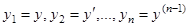, получим

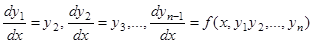. (3)

Система (3) есть частный случай системы (1).

Отметим, что сведение нормальной системы к одному дифференциальному уравнению 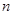-го порядка возможно далеко не всегда. Случаи, когда такое сведение возможно, будут рассмотрены ниже.