ОБЗОР ЭКСПЕРЕМЕНТАЛЬНОЙ ИНФОРМАЦИИ РАБОТОСПОСОБНОСТИ И НАДЕЖНОСТИ МЕХАНИЧЕСКИХ УСТРОЙСТВ
1.1 Общие сведения
Всю информацию, получаемую в результате эксперимента или наблюдений при эксплуатации, стендовых и лабораторных испытаний можно разбить на два класса.
1. Детерминированная информация. Детерминизм [7] – изучение о всеобщей причинной обусловленности закономерной связи всех явлений. Следовательно, детерминированная информация – это информация о физико-химических механических, электрических и других физических процессах, протекающих в изучаемых объектах. Наиболее распространенными физическими процессами старения технических устройств являются: износ кинематических узлов трения, потеря механической прочности под воздействием статических и циклических нагрузок, коррозия различных видов, прогрессирующие ухудшение функциональных свойств (так называемая параметрическая надежность изделий: например, потеря мощности двигателя, точности станка, подъемного усилия у домкрата) и т.п.
2. Статистико-вероятностная информация. В данном случае регистрируются не причинны и динамика протекающих процессов, а фиксированные состояния – следствия процессов в предположении, что их наступление и протекание носит случайный характер.
Для обработки и математической интерпретации этой информации существенную роль играют частота появления регистрируемых состояний (событий), геометрический вид распределения этих частот в выбранной системе отсчета.
По любому виду старения возможно получение информации обоих выше названных классов, причем каждый класс информации имеет свои достоинства и недостатки. Статистико-вероятностная информация полно учитывает влияние внешней среды эксперимента на результирующий показатель. Получаемая при этом информация полно учитывает влияние внешней среды эксперимента на результирующий показатель. Но получаемая при этом оценка является формальной и не отражает физическую сущность протекающих в изделии процессов.
Детерминированная информация по своей природе является физической. Она позволяет следить за физикой процесса, управлять и корректировать получаемые результаты. Однако получение этой информации является весьма трудоемким делом. Еще труднее воспроизводить условие эксперимента, т.е. получать стабильно повторяющуюся информацию.
1.2 Детерминированные зависимости процессов старения и работоспособности элементов технических устройств
Среди физико-химических процессов старения, первенство по наибольшему числу проявлений и наличию экспериментальных данных следует отдать износу. Это объясняется сравнительно легкой наблюдаемостью, простотой измерения с одной стороны, значительным числом элементов трения, применяемых в современной технике, с другой стороны.
Кривые износа (рис. 1.1) представляют весовые характеристики приработочного износа цифры в зависимости от времени приработки и способа обработки сопряженных поверхностей. Кривые имеют одну точку перегиба и одинаковый геометрический вид.
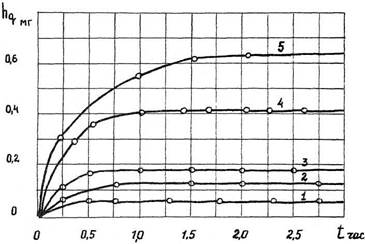
Рис. 1.1. Кривые весового износа цапфы в зависимости от времени работы при различных технологических приемах обработки поверхности.
На рис. 1.2. приведены кривые зависимости линейного износа втулок шатунов тракторных двигателей при различных шероховатостях сопряженных поверхностей. Кривая 3 отличается от других (рис. 1.1) появлением второй точки перегиба.
Кривые износа токарного резца по главной задней грани в зависимости от пути резанья (рис. 1.3) получены при точении серого чугуна СЧ 12-24 резцом твердого сплава ВК-8 при различных подачах режущего инструмента. Эти кривые имеют по две точки перегиба. Анализируя данные кривые, можно разработать модель типичной кривой износа. Термин “типичная кривая износа” впервые сформулирована А.Н. Ереминым [8] (рис. 1.4). Участками наибольшей кривизны кривая разделяется на три участка: 1 – приработочного износа, 2 – участок нормального рабочего износа, 3 – участок катастрофического износа.
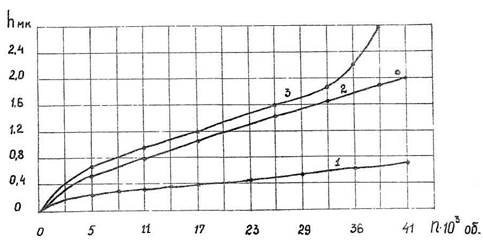
Рис. 1.2 Зависимость линейного износа втулок шатунов тракторных двигателей при различных шероховатостях сопряженных поверхностей.
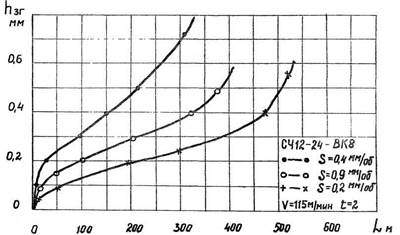
Рис. 1.3. Зависимость линейного износа твердосплавного резца по задней грани от пути резанья.
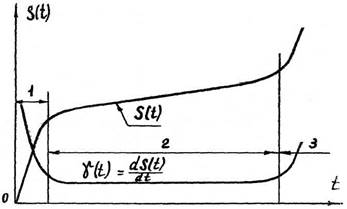
Рис. 1.4 Типичная кривая износа и скорости износа.
В работе [6] кривая износа, имеющая два участка наибольшей кривизны (три участка), именуется полной кривой износа, а кривые не имеющие участка 3 (а иногда и участка 1) - неполными кривыми износа.
Типичные виды кривых коррозийного старения (обобщенны М.А. Толстой) построены в координатах коррозия - время (рис. 1.5а) и скорость коррозии – время (рис. 1.5б).
Визуальный анализ показывает, что многие кривые износа геометрически весьма сходны с кривыми (рис. 1.5).
Следовательно, есть основание сделать предположение о наличии общих закономерностях механики процессов старения, несмотря на различную физико-химическую сущность протекающих процессов.
Аналогичного вида зависимость имеют место при процессах усталостного старения (рис. 1.6). По сравнению с ранее приведенными, эти кривые имеют “перевернутый” вид, что объясняется принятой системой отсчета. В приведенном случае учитывалось уменьшение первоначального запаса прочности. Для аппроксимирования экспериментальных кривых такие изменения вида кривых принципиального значения не имеют.
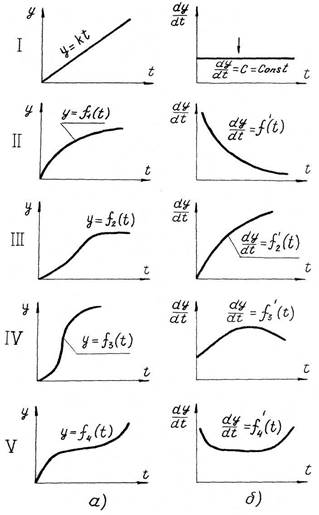
Рис. 1.5
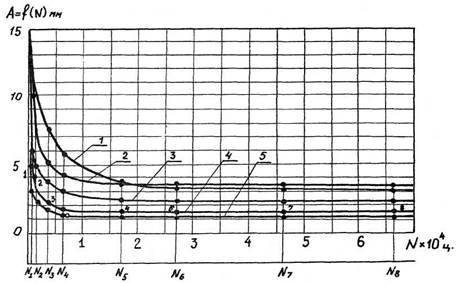
Рис. 1.6. Зависимости изменения амплитуды колебания пружинного маятника A = f(N), полученные при испытании до разрушения пяти образцов в одинаковых условиях.
1.3 Статистико-вероятностные зависимости надежности технических устройств.
Для оценки надежности технических устройств разрабатываются различные аналитические модели на базе непрерывных дискретных распределений случайных величин. Наиболее употребимыми являются непрерывные распределения.
В самом общем случае эти зависимости можно представить
1) функцией надежности, называемой функцией вероятности о безотказной работы объекта в момент времени t [4, 5]:
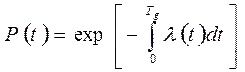 (1.1)
(1.1)
где P(t) – вероятность безотказной работы объекта в момент времени t; Tg – время, по истечении которого P(t) = 0 (предельный ресурс работы объекта); λ(t) – функция интенсивности отказов [4, 5];
2) функцией надежности, называемой также функцией распределения вероятности отказов объекта в момент времени t:
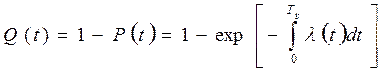 (1.2)
(1.2)
Часто в качестве модели используется плотность вероятности, представляющая собой первую производную от функции вероятности отказов:
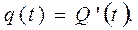 (1.3)
(1.3)
Вид функций распределения, который называют законом распределения, определяется функцией интенсивности отказов. Самый простой случай будет иметь место при λ(t)= λ = Const. (1.4)
В этом случае будет иметь место так называемое экспоненциальное распределение. Его уравнения имеют вид
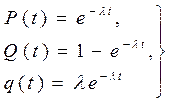 (1.5)
(1.5)
Геометрический вид функции экспоненциального распределения приведен на графиках (рис. 1.7). Экспериментальная информация предоставляется в виде протоколов испытаний или в виде гистограмм.
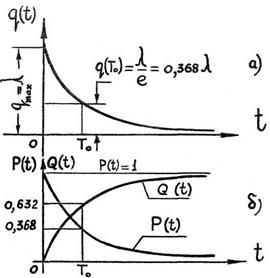
Рис. 1.7
Гистограмма интенсивности λN(t), определенная экспериментально (рис. 1.8), с достаточно хорошей точностью показывает, что λN(t) ≠ Const, распределение практически не является экспоненциальным, Методика обработки информации и построения подобных гистограмм будет рассмотрена ниже.
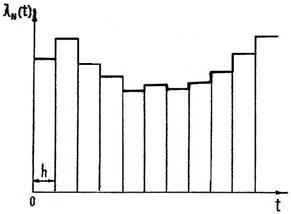
Рис. 1.8
Интенсивность отказа, выражение степенной функции вида
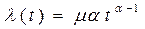 , (1.6)
, (1.6)
приводит к распределению Вейбулла – Гнеденко [4, 5, 9].
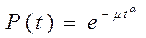 (1.7)
(1.7)
В формулах (1.6) и (1.7) μ и α – параметры распределения. Распределения Вейбулла – Гнеденко практически позволяет путем подбора параметров μ и α описать большинство кривых.
Видно (рис. 1.9), что экспоненциальное распределение является частным случаем распределения Вейбулла – Гнеденко при α = 1.
Для оценки надежности применяется и нормальное распределение. Его основные аналитические зависимости следующие:
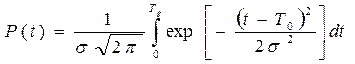 (1.8)
(1.8)
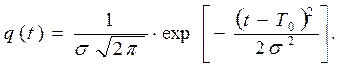 (1.9)
(1.9)
В формулах (1.8) и (1.9) T0 , σ – параметры распределения.
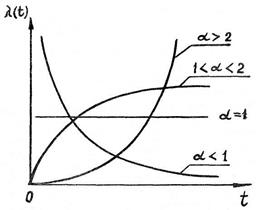
Рис. 1.9. Вид кривой интенсивности отказов распределения Вейбулла – Гнеденко при различных значениях α.
В работе [6] показано, что детерминированные и статические зависимости для одних и тех же условий старения являются подобными. В общем виде функция работоспособности имеет вид.
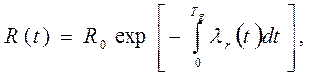 (1.10)
(1.10)
где Ro – начальный запас работоспособности; λr(t) – детерминированный аналог интенсивности отказов. Детерминированная функция старения имеет следующий вид:
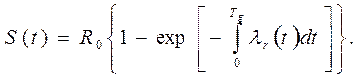 (1.11)
(1.11)
Уравнение (1.10) и (1.11) подобны уравнениям (1.1) и (1.2), константой подобия является Ro.
Краткое знакомство с информацией о надежности и работоспособности, а также об их взаимосвязи и подобии еще раз подчеркивает важность научных способов обработки, в том числе и аппроксимации.
2 НЕКОТОРЫЕ СВЕДЕНИЯ ПО ТЕОРИИ АППРОКСИМАЦИИ ГРАФИЧЕСКИХ ФУНКЦИЙ
2.1 Общие сведения.
Аппроксимация в качестве своих составных элементов предусматривает два комплекса приемов.
1.Установление и формирование общего вида и структуры уравнений. Определяется вид, число членов и структура уравнения.
2.Вычесление по экспериментальным данным параметров формул, дающих наилучшее приближение к результатам эксперимента.
Большинство современных работ [2, 10 - 12], рассматривая вопросы аппроксимации, в качестве формул принимают алгебраические уравнения: полином Лагранжа, степенную, показательную и другие функции. Необходимо отметить, что до настоящего времени не разработано алгоритма “угадывания” вида формул и ее структуры. Специалисту, занимающемуся аппроксимированием, необходимо знать вид и структуру уравнений, используемых в той области науки и технике, которой он занимается, и нередко интуитивно применять их.
Как известно, уравнениями работоспособности и надежности являются трансцендентные функции. В данной работе рассматриваются непрерывные дифференцируемые трансцендентные функции.
Особенности этих уравнений заключаются в их трудной разрешимости относительно искомых параметров. В ряде случаев возможны только приближенные решения.
Для нахождения параметров выбранных уравнений в настоящие время применяются способ выбранных точек, метод выравнивания кривых и метод наименьших квадратов [10, 12].
2.2 Способы выбранных точек.
Сущность названного способа заключается в следующем. На аппроксимируемой кривой произвольно выбирается ряд точек таким образом, чтобы их количество в 1,5 – 2 раза превышало число неизвестных параметров уравнения. Для них записывается система уравнений:
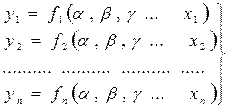 (2.1)
(2.1)
В уравнениях (2.1) yi, xi – известные значения аргумента и функций, соответствующие выбранным точкам на графике; α, β, γ – искомые параметры уравнения. Решая уравнения (2.1) относительно искомых параметров, устанавливают их численные значения:
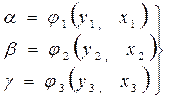 (2.2)
(2.2)
и т.д.
Способ выбранных точек имеет невысокую точность, так как точки выбирают наугад. В соответствии с принципом Лежандра [10] параметры α, β, γ по уравнениям (2.1) вычисляются 2 - 3 раза, для чего выбирается избыточное число точек. Способы вычисления и уточнения полученных результатов будут рассмотрены ниже.
2.3 Методы выравнивания кривых.
Данный метод является существенно более точным, но имеет ограниченное применение. Сущность его заключается в преобразовании уравнения для понижения порядка или приведения уравнения к известному. Наиболее простым и применяемым способом является линеаризация. Например, нелинейное уравнение вида
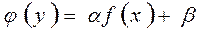 (2.3)
(2.3)
заменой переменных можно привести к виду
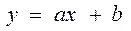 (2.4)
(2.4)
Уравнение (2.4) представляет собой прямою линию и его параметр легко определяется.
К этому же методу можно отнести более сложные замены экспериментальной кривой, например аппроксимацию параболой, окружностью и т. д.
2.4 Метод наименьших квадратов.
Метод наименьших квадратов имеет репутацию наиболее точного, но и более трудоемкого с точки зрения техники вычислений. И в этом случае предполагается, что вид уравнения известен:
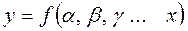 (2.5)
(2.5)
Должны быть вычислены также все отклонения от средних значений функции при соответствующем значении аргумента:
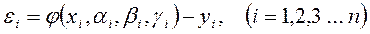 (2.6)
(2.6)
Наилучшими коэффициентами α, β, γ считаются те, при которых сумма квадратов отклонений будет минимальной.
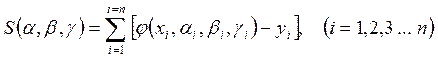 (2.7)
(2.7)
Используя условия экстремума, можно получить нормальную систему уравнений для определения коэффициентов:
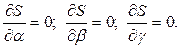 (2.8)
(2.8)
Значения α, β, γ удовлетворяющие уравнению (2.8), будут искомыми коэффициентами.
3 ПРАКТИЧЕСКИЕ ПРИМЕРЫ АППРОКСИМАЦИИ КРИВЫХ РАБОТОСПОСОБНОСТИ И НАДЕЖНОСТИ.
3.1 Линейная аппроксимация экспериментальных кривых.
Аппроксимация экспериментальных кривых старения уравнениями прямых известно уже давно. Особенно часто оно применяется для аппроксимации кривых износа. Кривую линию или семейство экспериментальных точек заменяют прямой линией (рис. 3.1 экспериментальные кривые выполнены пунктиром, а аппроксимирующие сплошными линиями).
В ряде случаев экспериментальную кривую заменяют прямой 1, проходящей через начало координат (рис. 3.1).
В этом случае аппроксимирующее уравнение будет иметь вид:
y =K x (3.1.)
где
K = γср = tg β (3.2.)
является средней скоростью старения объекта.
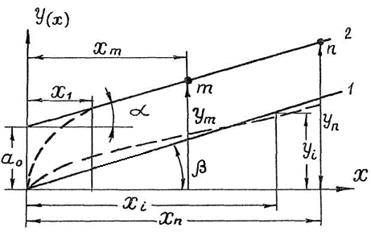
Рис.3.1.
При вычислениях необходимо иметь в виду, что соотношение (3.2) справедливо, если масштабы по осям x и y будут одинаковы. В противном случае коэффициент “К” будет пропорционален tg α, но не равен.
Параметр уравнения γср находится непосредственно по графику измерением угла β, или по измеренным абcциccе xi и ординате yi, с последующим вычислением γср = xi / yi.
Более сложной является аппроксимация уравнением прямой 2, не проходящей через начало координат (рис. 3.1). Уравнение этой прямой имеет вид
y =a0 + K x (3.4)
где К – имеет тоже смысл, что и в уравнение (3.1), параметр легко находится из графика 2 (рис. 3.1). При x = 0, y = a0.
Необходимо иметь в виду, что на интервале x1 расчет по уравнению (3.4) будет иметь значительную погрешность. На этом участке линейная аппроксимация является неприемлемой.
Можно для аппроксимации воспользоваться и уравнением прямой, проходящей через две точки. Если на кривой 2 (рис. 3.1) выбрать две точки m и n, то уравнение аппроксимации прямой можно записать в виде
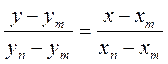 (3.5)
(3.5)
Параметры K и α, можно выразить следующим образом:
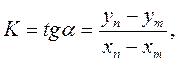 (3.6)
(3.6)
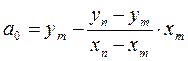 (3.7)
(3.7)
Линейная аппроксимация в задачах надежности и работоспособности применяется для нахождения параметров ряда линейных распределений, плотностей, интенсивности и их детерминированных аналогов. Линейная аппроксимация широко применяется в силу своей просторы и доступности. Однако это представление маскирует сущность происходящих явления и на ряде интервалов по оси абсцисс является весьма неточным.
3.2 Аппроксимация простейших кривых с одним участком наибольшей кривизны.
К простейшим кривым относятся кривые старения или работоспособности, имеющие один участок наибольшей кривизны (рис. 1.1). Они могут быть выпуклы как вверх, так и вниз. Это не имеет принципиального значения для нахождения величины параметров.
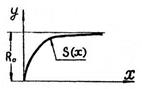
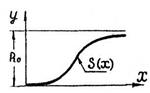
По геометрическому виду кривая hg (рис. 3.2.) – это неполная кривая износа с одним участком наибольшей кривизны. Кривая стремится к некоторой постоянной величине h – асимптоте.
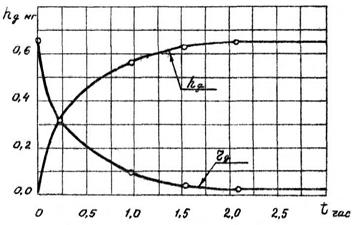
Рис. 3.2
Следовательно, физически h представляет собой начальный запас физических возможностей объекта, а кривая hg показывает количество израсходованных физических свойств объекта в любой момент времени. Символ будет иметь смысл начального запаса материала (объема, линейной величины), конструктивно предназначенного для износа от начала эксплуатации до полного выхода изделия из строя.
Поэтому кривая hg названа детерминированной кривой старения [6].
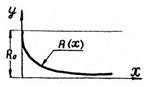
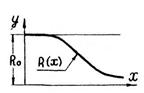
Кривая rg, называемая кривой работоспособности объекта [6], является дополняющей кривой к hg. Это означает, что в любой момент времени выполняется следующее условия:
rg + hg = h0 = Const. (3.8)
Из этого краткого анализа следует, что, аппроксимируя кривую hg или rg, можно решить ряд задач и в первую очередь задачу вычисления начального уровня работоспособности по результатам эксперимента.
Рассмотрим ряд соображений по определению (“угадыванию”) структуры уравнений работоспособности и старения. Из литературы [4 – 6, 9] известно, что основным уравнением непрерывных законов работоспособности и надежности является уравнение
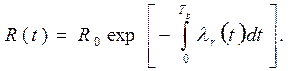 (3.9)
(3.9)
При R0 = 1 уравнение (3.9) будет являться статистической функцией надежности – вероятности безотказной работы.
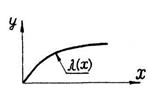
Вид кривой определяет подлинность подинтегральной функцией λr(t). Как указывалось выше, большинство экспериментальных кривых работоспособности и надежности можно аппроксимировать распределением Вейбулла – Гнеденко. В табл. 3.1 приведены основные уравнения старения и работоспособности, выведенные при условии, что старение подчиняется закону Вейбулла – Гнеденко.
Анализ показывает, что практически любые виды кривых могут быть описаны приведенными уравнениями. Рассмотрим конкретный пример аппроксимации.
По геометрическому виду кривая b (рис. 3.3) – это неполная кривая износа. Предполагаемым уравнением при α = 1 может быть экспоненциальное уравнение (табл. 3.1)
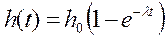 (3.10)
(3.10)
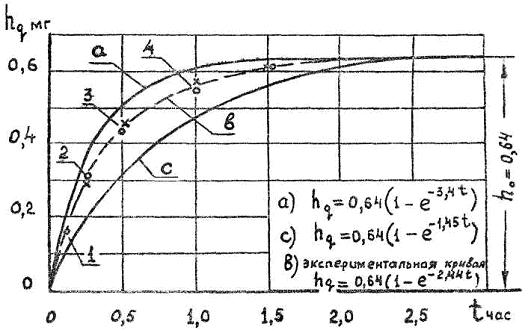
Рис 3.3
Аппроксимирование будет заключаться в отыскании значений h0, и λ, наилучшим образом описывающих экспериментальную кривую. Оно может осуществляться различными приемами и технологией вычислений. Как правило, результаты вычислений будут нередко существенно отличаться друг от друга. Задача вычислений найти наиболее точный вариант вычисления искомых параметров.
Таблица. 3.1
Виды кривых аппроксимирующие формулы при процессах работоспособности и старения, описываемых законом Вейбулла – Гнеденко и экспоненциальным.
| Примеры кривых и формул старения | Примеры кривых и формул | Примеры кривых безразмерной скорости старения | Значения параметров для данного вида кривых |
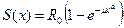
| 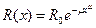
| 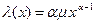
| |
| 
| 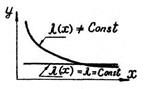
| Геометрический параметр 0 < α ≤ 1 Масштабный параметр μ > 0 |
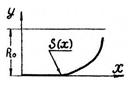
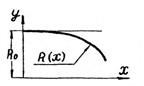
| 
| 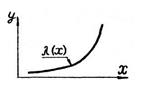
| α > 2, μ > 0 |
| 
| 
| 1 < α < 2, μ > 0 |
Геометрический вид кривой определяет экспоненциальная структура уравнения и частично параметр λ. Параметр h0, с геометрической точки зрения является асимптотой и с хорошей степенью точности может быть принят из графика. Из графика (рис. 3.3) определяем h0 = 0,64.
Для определения λ воспользуются методом выбранных точек (рис.3.3). Выбираем пять точек; точки следует выбирать на участке с наибольшей кривизной.
В соответствии с принципом Лежандра [10] число точек должно быть больше числа разыскиваемых неизвестных. Это необходимо для уточнение вычисленных значений параметров.
Первый вариант нахождения параметров уравнения.
Запишем в общем виде для выбранных на графике точек (рис. 3.3) уравнения (3.10):
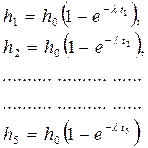 (3.11)
(3.11)
Определим λ из двух соседних уравнений (3.11):
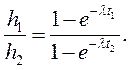 (3.12)
(3.12)
После преобразования получим
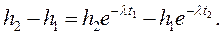 (3.13)
(3.13)
Обозначим x1 = - λ t1; x2 = - λ t2 и подставим в уравнение (3.14):
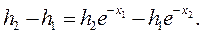 (3.14)
(3.14)
Приближенное решение уравнения (3.14) можно получить, разложив в ряд и взяв два значащих члена:
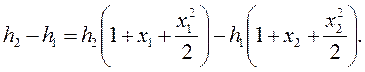 (3.15)
(3.15)
После подстановок и преобразований получим
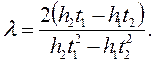 (3.16)
(3.16)
Данное решение является весьма приближенным, и наилучшее приближение имеет место на начальном участке кривой.
Данные расчета λi по формуле (3.16) приведенные в таблице 3.2.
Таблица 3.2
| №№ точек | ti | hi | λi | Проверочный расчет по уравнению
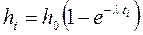
| Разность вычисленных и измерен. значений | % | |||
| ti 2,42 | 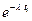
| 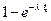
| hi | ||||||
| 0,125 | 0,23 | 3,4 | 0,3025 | 0,7389 | 0,2611 | 0,167 | -0,063 | 27,4 | |
| 0,25 | 0,33 | 0,605 | 0,5461 | 0,4539 | 0,290 | -0,04 | 12,1 | ||
| 0,125 | 0,23 | 2,39 | - | - | - | - | - | - | |
| 0,5 | 0,43 | 1,21 | 0,2982 | 0,7018 | 0,449 | +0,019 | 4,4 | ||
| 0,125 | 0,23 | 1,45 | - | - | - | - | - | - | |
| 1,0 | 0,55 | 2,42 | 0,0889 | 0,9111 | 0,583 | +0,033 | 6,0 | ||
| 0,125 | 0,23 | 0,127 | - | - | - | - | - | - | |
| 2,5 | 0,62 | 6,05 | 0,0023 | 0,9977 | 0,638 | +10,018 | 2,9 |
Как видно из табл. 3.2 значения λi увеличиваются при приближении точек к началу координат. Это следует из математической сущности разложения в ряд. Аппроксимирующая кривая а (рис. 3.3) построена по уравнению (3.10) при h0 = 0,64, λi = 3,4. Она прошла выше экспериментальной. При h0 = 0,64, λi = 1,45 кривая с (рис. 3.3) прошла ниже экспериментальной. Отбросим значения λi = 0,127, как явно выпадающее из ряда других, и определим среднее арифметическое
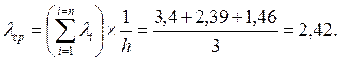 (3.17)
(3.17)
При λ = 2,42 имеет место наилучшее приближение к результатам эксперимента (рис 3.3, показанного крестиками). Аппроксимирующее уравнение будет иметь вид
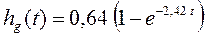 (3.18)
(3.18)
Первая производная
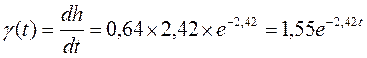 (3.18)
(3.18)
В табл. 3.2 приведены результаты контрольного расчета значений по уравнению (3.18). Как видно из сравнения вычисленных и измеренных значений, наблюдаются существенное несовпадение, особенно на начальном участке кривой.
Алгоритм аппроксимации для вышеприведенного примера будет содержать следующие приемы:
1. По результатам эксперимента строится кривая и осуществляется ее геометрическое аппроксимирование (проводится линия, наилучшим образом соединяющая точки).
2. Определяется асимптота ho из графика. Можно ho вычислить решением любого уравнения (3.11), но после определения и усреднения λ.
3. Выбираются точки, не менее четырех, таким образом, чтобы большинство их были на участке с наибольшей кривизной. Составляется таблица значений ti и hi.
4. Вычисляются значения λi для различных пар точек по уравнению (3.16) и заносятся в табл. 3.2.
5. Резко отличные значения λi отбрасываются, по остальным вычисляется среднеарифметическое.
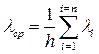 (3.19)
(3.19)
6 Для проверки или определения ho, если это необходимо, можно воспользоваться уравнением
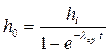 (3.20)
(3.20)
Второй вариант расчетов
Первый вариант аппроксимации показал, что для повышения точности аппроксимирования в первую очередь наиболее важно определить величину ho – координату горизонтальной асимптоты. К сожалению, соответствующий раздел математически разработан очень слабо.
Асимптоту можно с достаточной точностью определить из графика (рис. 3.3). В этом случае уравнение (3.10) можно преобразовать следующим образом:
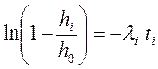
откуда
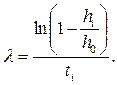 (3.21)
(3.21)
В табл. 3.3 приведены результаты расчета hi и λi по уравнению (3.21) и проверочные вычисления.
Таблица 3.3
| №№ точек | ti | hi | 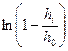
| λi | Проверка 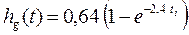
| |||
| 2,4 ti |
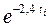
| hi расч | Разность Значений изм. и расч. | |||||
| 0,125 | 0,23 | -0,4447 | 3,55 | 0,3 | 0,7408 | 0,165 | -0,065 | |
| 0,25 | 0,33 | -0,7236 | 2,89 | 0,6 | 0,5488 | 0,288 | -0,042 | |
| 0,5 | 0,43 | -1,1147 | 2,23 | 1,2 | 0,3011 | 0,447 | +0,017 | |
| 0,55 | -1,9589 | 1,95 | 2,4 | 0,0907 | 0,582 | +0,032 | ||
| 2,5 | 0,62 | -3,4420 | 1,37 | 6,0 | 0,0024 | 0,638 | +0,018 |
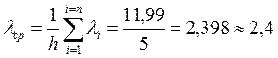
Как видно из приведенных данных, результаты получились близкими полученными по первому варианту и практически с таким же несовпадением с измеренными значениями.
Третий вариант
К нему необходимо прибегнуть, если не устраивает точность аппроксимации по первым двум вариантам. Попробуем повысить точность аппроксимации, усложним уравнение (3.10) с помощью распределения Вейбулла – Гнеденко [4]:
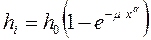 (3.22)
(3.22)
Преобразуем уравнение (3.22) к виду
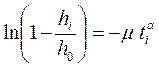 (3.23)
(3.23)
Поделим уравнения двух соседних точек друг на друга, прологарифмируем еще раз
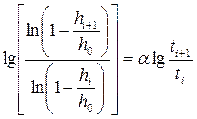 (3.24)
(3.24)
отсюда
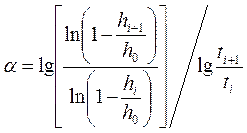 (3.25)
(3.25)
По формуле (3.25) произведен расчет αi и αср кривой (рис.3 3) при ho = 0,64, результаты приведены в табл. 3.4.
Таблица 3.4
| №№ точек | ti | hi | 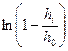
| 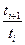
| 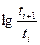
| 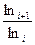
| 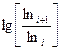
| αi |
| 0,125 | 0,23 | -0,4447 | ||||||
| 0,25 | 0,33 | -0,7236 | 2,0 | 0,30103 | 1,6272 | 0,2114 | 0,702 | |
| 0,5 | 0,43 | -1,1147 | 2,0 | 0,30103 | 1,5405 | 0,1876 | 0,623 | |
| 0,55 | -1,9589 | 2,0 | 0,30103 | 1,7573 | 0,2448 | 0,813 | ||
| 2,5 | 0,62 | -3,4420 | 2,5 | 0,39794 | 1,7571 | 0,2447 | 0,615 |
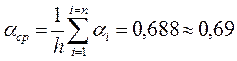
Из уравнения (3.23) следует, что
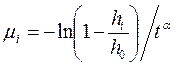 (3.26)
(3.26)
В тбл.3.5 приведен расчет μi по формуле (3.26).
Таблица 3.5
| №№ точек | ti | hi | 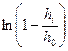
| 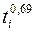
| μi | Проверка | ||
| 1,87ti0,69 | hi | Разность Значений изм. и расч. | ||||||
| 0,125 | 0,23 | -0,4447 | 0,2381 | 3,55 | 0,4452 | 0,230 | ||
| 0,25 | 0,33 | -0,7236 | 0,3842 | 2,89 | 0,7184 | 0,328 | 0,002 | |
| 0,5 | 0,43 | -1,1147 | 0,6198 | 2,23 | 1,1590 | 0,4391 | 0,009 | |
| 0,55 | -1,9589 | 1,0 | 1,95 | 1,87 | 0,5413 | 0,0087 | ||
| 2,5 | 0,62 | -3,4420 | 1,8818 | 1,37 | 3,5189 | 0,6210 | 0,001 |
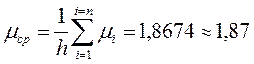
Искомое уравнение: 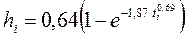
Как видно из данных (табл. 3.5), несовпадения результатов измерения и расчета по уравнению не превышает 2%, что позволяет считать точность аппроксимации очень высокой.
3.3 Аппроксимация кривой интенсивности отказов.
Рассмотрим еще одну разновидность кривой старения. На рис. 3.4 приведена экспериментальная кривая интенсивности отказов распределения Вейбулла – Гнеденко.
Как известно, структура формулы будет иметь вид
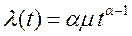 (3.27)
(3.27)
причем предварительно можно указать, что 0 < α <1.
Для аппроксимации воспользуемся методом выравнивания. Для этого нанесем экспериментальные данные на двойную логарифмическую сетку (рис. 3.5). Видно, что точки расположились на прямой лини. В этом состоит и сущность выравнивания, т.е. замены сложной кривой более простой прямой линий.
Прологарифмируем уравнение (3.27):
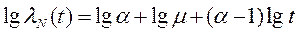 (3.28)
(3.28)
Уравнение (3.22) является уравнением прямой линии, не проходящей через начало координат. Выражение в скобках является угловым коэффициентом. Следовательно, измерения углов β (рис.3.5) получим
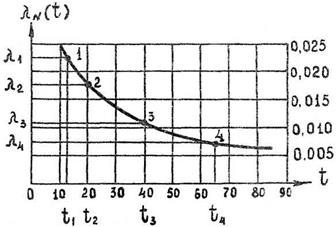
Рис. 3.4. Пример аппроксимации кривой интенсивности отказа.
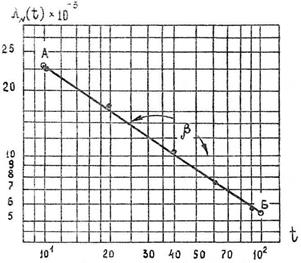
Рис. 3.5. Аппроксимация кривой интенсивности отказов
методом выравнивания.
 ( 3.29)
( 3.29)
откуда α = 0,3506.
Получим этот же результат методов выбранных точек (рис.3.4). Для этих точек уравнение (3.27) запишется следующей системой уравнений:
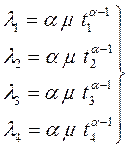 (3.30)
(3.30)
Из любых двух уравнений системы (3.30) следует, что
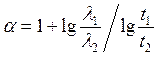 (3.31)
(3.31)
Данные вычисления α по уравнению (3.31) приведены в табл. 3.6.
Таблица 3.6
| №№ точек | 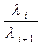
| 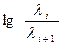
| 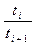
| 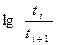
| 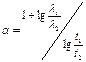
|
| 1; 2 | 1,285 | 0,1099 | 0,65 | -0,1871 | 0,413 |
| 2; 3 | 1,59 | 0,2014 | 0,5 | -0,3010 | 0,331 |
| 3; 4 | 1,57 | 0,1959 | 0,615 | -0,2111 | 0,073 |
| 4; 5 | 2,045 | 0,3096 | 0,325 | -0,4881 | 0,366 |
Воспользовавшись уже известной рекомендацией об отбрасывании выпадающего значения, определим среднее значение α.
αср = 0,370 (3.32)
Разность с полученными значениями α составляет меньше 10 т.е. находится в пределах точности измерения угла на графике (рис. 3.5).
Значение μ можно вычислить по уравнению.
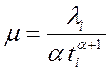 (3.33)
(3.33)
По данным (рис. 3.4 и табл. 3.6) значение μ вычислены по формуле (3.33) и приведены в табл. 3.7.
Таблица 3.7
| №№ точек | ||||
| μ | 0,3060 | 0,3122 | 0,3037 | 0,2624 |
Отбросив значения 0,2624 и, вычислив среднеарифметическое, получим
μср = 0,3073 (3.34)
При использовании метода выравнивания удобно выбрать точки А и Б (рис. 3.5), для которых уравнение (3.28) записывается в виде
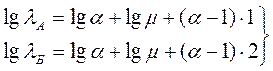 (3.35)
(3.35)
Сложив оба уравнения, легко можно выразить μ.
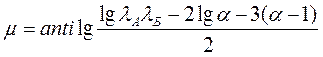 (3.36)
(3.36)
Как видно из приведенного выше примера, метод выравнивания значительно точнее и менее трудоемок. Необходимо отменить, что не всегда удается линеаризовать аппроксимируемое уравнение или экспериментальную кривую. Разыскиваемое в приводимом примере уравнение будет иметь вид
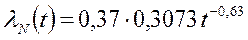 .
.
3.4 Аппроксимация методом наименьших квадратов.
Для изучения сущности метода наименьших квадратов рассмотрим один простейший пример аппроксимирования.
Экспериментальная зависимость старения простейшего вида (рис 3.6) имеет вид S(t) = k∙t (3.37)
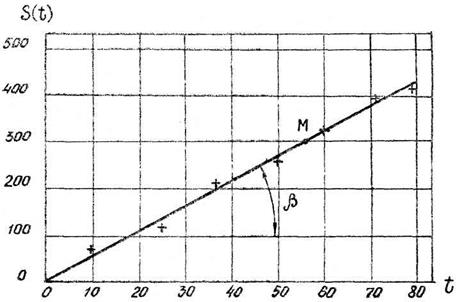
Рис. 3.6. Пример аппроксимации методом наименьших квадратов.
Угловой коэффициент K определяется элементарно:
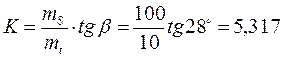 (3.38)
(3.38)
В формуле (3.38) ms, mt – масштабные коэффициенты необходимо тогда, года по осям S и t используются разномасштабные шкалы.
Следовательно, уравнения прямой (рис. 3.6) будет иметь вид
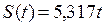 (3.39)
(3.39)
Теперь определим значения параметра К из условия минимума суммы квадратов отклонений аппроксимирующих значений 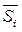 от экспериментальных Si.
от экспериментальных Si.
Это формулируется следующ
| <== предыдущая лекция | | | следующая лекция ==> |
| Современные требования | | |
Дата добавления: 2021-09-25; просмотров: 99;










