Числовой ряд и его сумма

Определение 1. Пусть задана бесконечная числовая последовательность

.

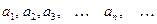Выражение

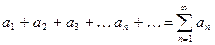(1)

называется числовым рядом, а числа 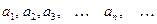называются членами ряда, при этом 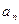называется n-ым (или общим) членом ряда.

Определение 2. Сумма 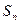n первых членов ряда (1)

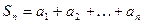
называется частной суммой ряда (1).

Например, ,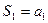

,

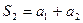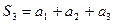и т.д.

Определение 3. Ряд

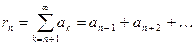(2)

называется n-ым остатком ряда (1). Он получен из ряда (1) после отбрасывания n первых членов этого ряда.

Таким образом, .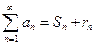

Примеры. 1) Дан ряд 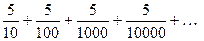. Найти .

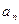Запишем данный ряд в виде 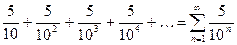, таким образом .

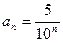2) Дан ряд 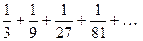. Найти , , .

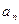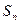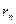Запишем данный ряд в виде 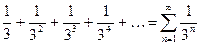. Тогда , , .

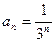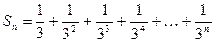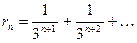Определение 4. Ряд называется сходящимся, если последовательность его частичных сумм сходится, т.е. существует конечный предел

.

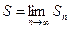Этот предел называется суммой ряда (1). Ряд называется расходящимся, если последовательность его частичных сумм расходится.

Основные теоремы о сходимости числовых рядов

Теорема 1. Если ряд сходится, то и любой его остаток сходится. Если какой-нибудь остаток сходится, то и ряд сходится.

Доказательство:

Пусть дан ряд 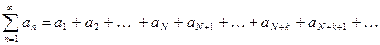. Обозначим частные суммы ряда следующим образом:

,

.

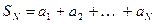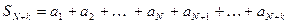Тогда для частных сумм ряда 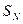и 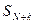верно равенство:

,

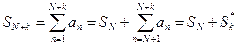где 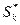- k-я частичная сумма N–го остатка ряда 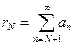. Таким образом,

,

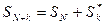где 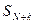- частная сумма ряда, 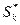- частная сумма остатка.

1) Пусть ряд 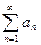– сходится, тогда 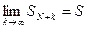, отсюда 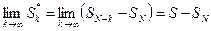, следовательно, остаток тоже сходится.

2) Пусть остаток – сходится, тогда 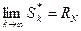, отсюда 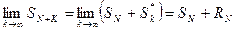, следовательно, ряд 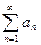сходится.

Теорема 2. Пусть ряды с общими членам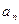и и 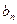сходятся, причём 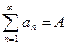, 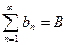. Тогда для любых чисел 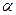и 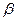ряд с общим членом 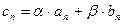сходится и .

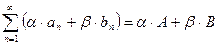Доказательство:

Найдём предел частной суммы 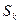ряда 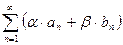и покажем, что этот предел конечен.

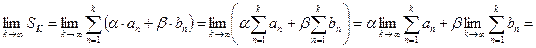
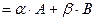
Таким образом, ряд 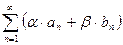сходится.

Пример. Вычислить сумму ряда .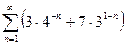

Запишем общий член ряда 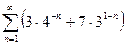в следующем виде 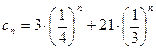. Тогда по теореме 2 ряд 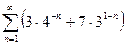сходится, если сходятся ряды 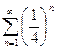и 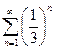. Оба ряда являются суммами бесконечных убывающих геометрических прогрессий, которые будем вычислять по формул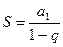е , где 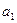- первый член ряда, 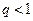- знаменатель прогрессии. Тогда

,

.

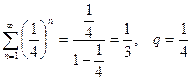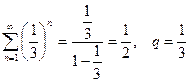Отсюда сумма ряда 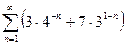равна:

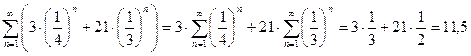
Теорема 3 (необходимый признак сходимости ряда). Если ряд 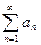сходится, то .

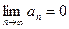Доказательство:

Пусть ряд 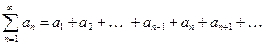сходится. Обозначим через 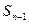и 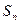следующие частные суммы ряда:

,

.

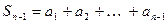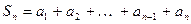Так как ряд 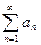- сходится, то 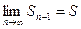, , 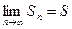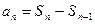. Тогда

.

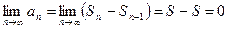Теорема доказана.

Замечания. 1) Необходимый признак сходимости не является достаточным.

Обратное, вообще говоря, неверно.

Пример. 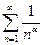– обобщённый гармонический ряд, если 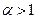– ряд сходится, если 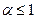– ряд расходится. Если 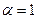, то ряд 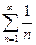расходится, но .

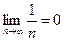2) Из формулировки теоремы 3 следует, что, если 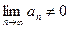, то ряд 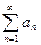расходится.

Примеры. 1) Исследовать на сходимость ряд .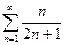

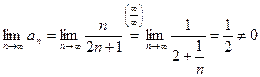, отсюда по необходимому признаку следует, что ряд 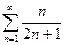расходится.

2) Исследовать на сходимость ряд .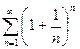

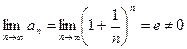, отсюда по необходимому признаку следует, что ряд 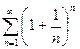расходится.

3) Исследовать на сходимость ряд .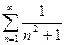

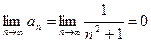, необходимый признак не даёт ответа на вопрос о сходимости ряда. Вопрос о сходимости ряда остаётся открытым.

ЛЕКЦИЯ 2. ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ

Признаки сходимости рядов с неотрицательными членами.

Теорема 1 (признак Коши). Пусть для ряда 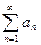с неотрицательными членами выполняется условие

.

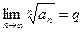Тогда, если q<1, то ряд сходится, а если q>1, то ряд расходится.

Замечание. Если 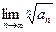не существует или равен единице, то признак Коши не даёт ответа на вопрос о сходимости ряда.

Примеры. 1) Исследовать на сходимость ряд .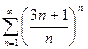

По признаку Коши получаем:

.

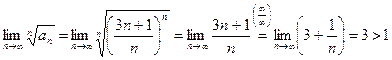Таким образом, ряд 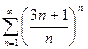расходится.

2) Исследовать на сходимость ряд .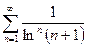

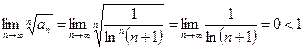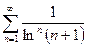Применяем признак Коши , ряд сходится.

Теорема 2 (признак Даламбера). Пусть для ряда 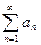с неотрицательными членами выполняется условие

.

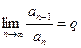Тогда, если q<1, то ряд сходится, а если q>1, то ряд расходится.

Замечание. Если 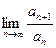не существует или равен единице, то признак Даламбера не даёт ответа на вопрос о сходимости ряда.

Примеры. 1) Исследовать на сходимость ряд .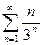

Применяем признак Даламбера:

, , .

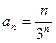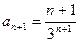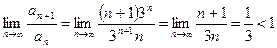Таким образом, ряд 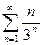сходится.

2) Исследовать на сходимость ряд .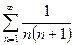

, , .

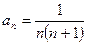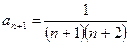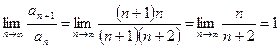Признак Даламбера не даёт ответа на вопрос о сходимости ряда.

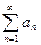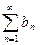Теорема 3 (признак сравнения). Пусть для рядов и выполняется условие: существует число N, такое, что 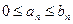для любого 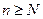. Тогда, если ряд 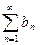сходится, то и ряд 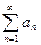сходится. Если же ряд 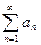расходится, то и ряд 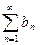расходится.

Примеры. 1) Исследовать на сходимость ряд .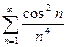

Применяем признак сравнения:

.

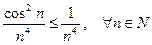Ряд 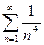сходится (обобщённый гармонический ряд, 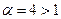), отсюда ряд 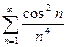тоже сходится.

2) Исследовать на сходимость ряд .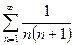

Сравниваем данный ряд с обобщённым гармоническим рядом :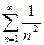

.

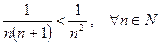Ряд 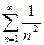сходится ( 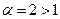), тогда по признаку сравнения ряд 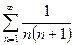тоже сходится.

Теорема 4 (интегральный признак Коши). Пусть функция 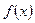задана на луче 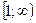, непрерывна, положительна, монотонно убывает и стремится к нулю при 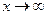. Обозначим 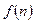через 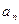( 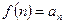). Тогда ряд 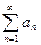сходится в том и только том случае, когда сходится несобственный интеграл .

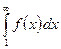Пример. Исследовать на сходимость ряд .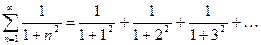

Общий член ряда равен 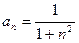, тогда получаем функцию 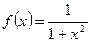, где .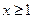

Функция :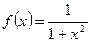

1) непрерывна для ;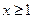

2) положительна для ;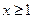

3) монотонно убывает на промежутке .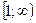

Вычислим несобственный интеграл:

.

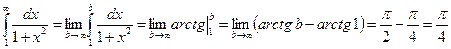Интеграл 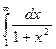сходится, тогда ряд 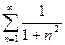тоже сходится.

Абсолютно и условно сходящиеся ряды. Теорема Лейбница

Членами абсолютно и условно сходящихся рядов являются любые действительные числа.

Примеры. 1) 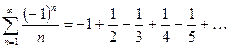– знакочередующийся ряд.

2) 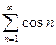– знакопеременный ряд.

Определение 1. Ряд 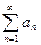называется абсолютно сходящимся, если сходится ряд его абсолютных величин .

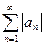Определение 2. Ряд 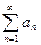называется условно сходящимся, если ряд 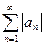расходится, а ряд 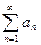сходится.

Теорема 1. Если ряд 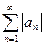сходится, то и ряд 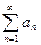сходится.

Для исследования рядов на абсолютную сходимость можно пользоваться всеми признаками сходимости для рядов с неотрицательными членами.

Примеры. 1) Исследовать на абсолютную сходимость ряд .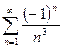

Для данного ряда получим ряд модулей 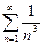, исследуем его на сходимость. Ряд модулей 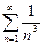является обобщённым гармоническим рядом. Так как степень знаменателя 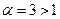, то ряд 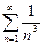сходится. Тогда по теореме 1 ряд 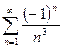сходится абсолютно.

2) Исследовать на абсолютную сходимость ряд .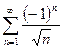

Ряд модулей 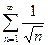, полученный для ряда 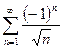, расходится (это обобщённый гармонический ряд, 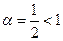). Теорема 1 не даёт ответа на вопрос о сходимости ряда 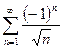. Для данного ряда следует применить признак Лейбница.

Теорема 2 (признак Лейбница). Если ряд :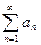

1) знакочередующийся;

2) члены ряда по модулю не возрастают, т.е. ;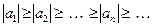

3) ;

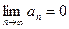то ряд 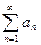сходится.

Пример. Исследовать на сходимость ряд .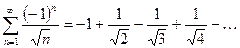

Как было показано выше, ряд модулей 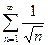расходится. Применяем к ряду признак Лейбница:

1) ряд знакочередующийся;

2) ;

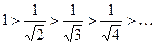3) .

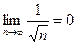Все условия теоремы 2 выполняются, следовательно, ряд 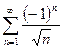сходится условно.

ЛЕКЦИЯ 3. ФУНКЦИОНАЛЬНЫЕ И СТЕПЕННЫЕ РЯДЫ

Функциональные ряды. Область сходимости

Определение 1. Пусть задана последовательность функций 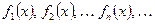, определённая на одном и том же множестве A. Ряды вида

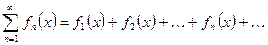(1)

называются функциональными.

При фиксированном значении 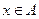из ряда (1) получаются числовые ряды, как сходящиеся, так и расходящиеся.

Пример.

Рассмотрим функциональный ряд 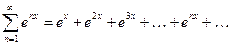. При x=1 из данного ряда получаем числовой ряд 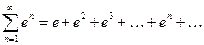, который является суммой геометрической прогрессии со знаменателем 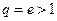. Частная сумма ряд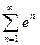а равна 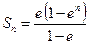, тогда найдём сумму ряда 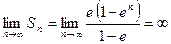. Следовательно, числовой ряд 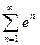расходится.

Определение 2. Совокупность тех значений 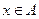, при которых функциональный ряд (1) сходится, называется областью сходимости ряда (1).

Пример. Найти область сходимости ряда .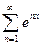

Сумма геометрической прогрессии существует, если знаменатель 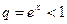. Отсюда следует неравенство 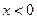, областью сходимости ряда является интервал 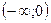. По формуле 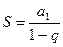для суммы бесконечной убывающей геометрической прогрессии находим сумму данного ряда 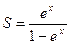, где .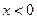

Понятие степенного ряда. Радиус сходимости. Теорема Абеля

Определение 1. Функциональные ряды вида

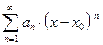(2)

где 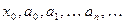– действительные числа, называются степенными рядами. Числа 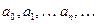называются коэффициентами степенного ряда (2).

Теорема Абеля. Если степенной ряд (2) сходится в точке 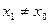. то он сходится абсолютно в любой точке x, такой, что 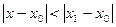. Если же ряд (2) расходится в точке 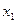, то он расходится в любой точке x, для которой .

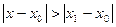По теореме Абеля получено, что для ряда (2) возможны 3 случая:

1) ряд (2) сходится только в точке ;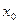

2) ряд (2) сходится для всех ;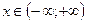

3) существует число 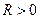, такое, что для всех x из интервала 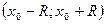ряд (2) сходится, а для всех x, таких, что 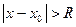, ряд (2) расходится.

Определение 2. Число 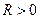, такое, что ряд (2) сходится для всех x, удовлетворяющих условию 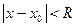, и расходится для всех x, удовлетворяющих условию 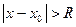, называется радиусом сходимости ряда (2).

Если ряд (2) сходится только в точке 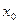, то 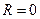; если ряд (2) сходится для 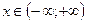, то .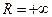

Теорема 2. Если у степенного ряда (2) последовательность 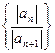имеет конечный или бесконечный предел, то для радиуса сходимости справедлива формула:

.

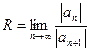Пример. Найти область сходимости ряда .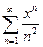

Находим радиус сходимости ряда:

.

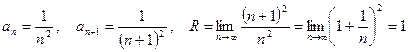Ряд сходится для 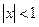, т.е. для -1<x<1, и расходится для .

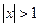Исследуем ряд на сходимость в точках x=1 и x=-1.

При x=1 получаем числовой ряд 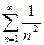, который сходится как обобщённый гармонический ряд ( ).

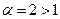При x=-1 получаем знакочередующийся ряд 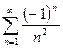, который абсолютно сходится, так как сходится его ряд модулей .

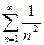Областью сходимости ряда является промежуток [-1;1].

Теорема 3. Пусть последовательность 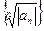имеет конечный или бесконечный предел. Тогда для радиуса сходимости справедлива формула:

.

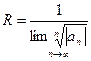Пример. Найти область сходимости ряда .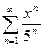

Находим радиус сходимости ряда:

.

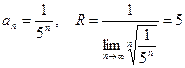Ряд сходится для 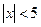, т.е. для -5<x<5, и расходится для .

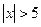Исследуем ряд на сходимость в точках x=5 и x=-5.

При x=5 получаем числовой ряд 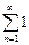, который расходится по необходимому признаку, так как .

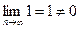При x=-5 получаем знакочередующийся ряд 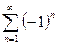, который также расходится по необходимому признаку, так как .

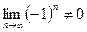Областью сходимости ряда является промежуток (-5;5).

Разложение функции в степенной ряд. Ряд Тейлора

Нахождение для данной функции 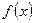степенного ряда 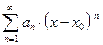, сумма которого есть функция 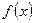, называется разложением функции 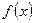в степенной ряд по степеням .

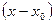Теорема 1. Если функция 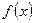разлагается в степенной ряд, то это разложение единственно.

Доказательство:

Пусть функция 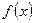является суммой степенного ряда 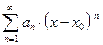в интервале 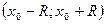, то есть:

.

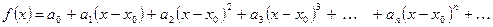Дифференцируем степенной ряд:

,

,

…………………………………………………………………..

,

…………………………………………………………………..

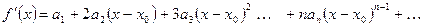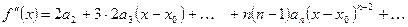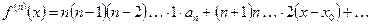Тогда

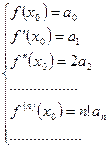
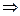
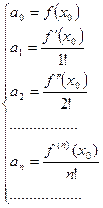
Таким образом, если функция 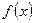разлагается на интервале 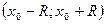в степенной ряд, то это возможно единственным способом:

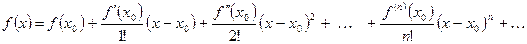(3)

Данный ряд называется рядом Тейлора функции 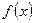в точке .

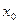Разложить в степенной ряд в окрестности точки 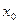можно только функцию, имеющую в точке 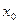производную 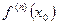любого порядка.

Достаточное условие разложимости функции в степенной ряд.

Теорема 2. Пусть функция 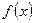имеет в точке 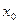производную 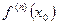любого порядка и 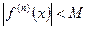на интервале 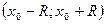, где M>0.Тогда ряд Тейлора функции 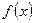сходится к 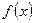на интервале .

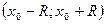Подставляя 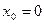в формулу (3), получаем ряд Маклорена:

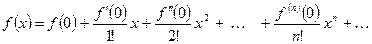(4)

Ряды Тейлора для элементарных функций

Выведем разложение в ряд для функции 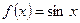. Используем формулу (4):

………………………… ……………….

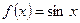
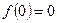
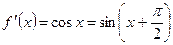
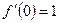
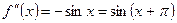
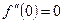
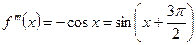
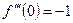
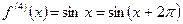
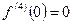
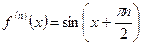
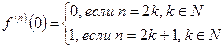
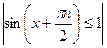- выполняется достаточное условие разложимости функции 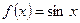в степенной ряд. Получаем разложение в ряд Тейлора функции :

.

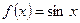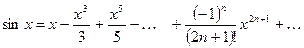Найдём область сходимости полученного ряда, используя признак Даламбера:

, ,

.

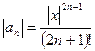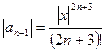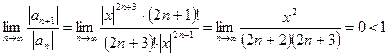Таким образом, ряд сходится абсолютно для всех .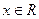

ЛЕКЦИЯ 4. РЯДЫ ФУРЬЕ

Системы ортогональных функций

Определение. Система функций 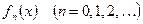называется ортогональной в промежутке (a;b) с весом p(x), если при всяком 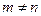имеет место равенство

,

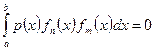где p(x) – некоторая фпксированная неотрицательная функция, не зависящая от индексов m и n.

Пример. Система функций 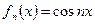, , 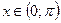p(x)=1, 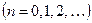, является ортогональной, так как при 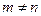получаем:

.

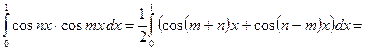
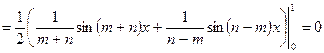Ортогональные системы функций играют большую роль, главным образом, в связи с возможностью разложения произвольных функций в ряды по ортогональным функциям, примером которых является ряд Фурье.

Ряды Фурье для периодических функций с периодом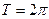

Рассмотрим ряд Фурье для периодической функции с периодом .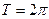

Определение. Тригонометрический ряд

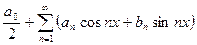, (1)

коэффициенты которого вычисляются по формулам

,

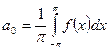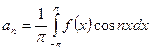, (2)

,

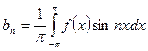называется рядом Фурье функции 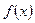, а коэффициенты 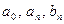называются коэффициентами Фурье функции .

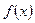Выведем формулы (2).

Доказательство:

Предположим, что ряд (1) сходится к функции f(x) на отрезке 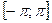, т.е. функция f(x) является суммой ряда (1):

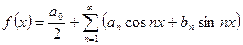. (3)

Предположим, что функция f(x) интегрируема на отрезке 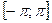, а ряд (1) можно интегрировать почленно. Проинтегрируем равенство (3) по x от 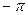до :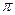

.

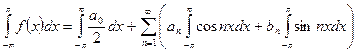Тогда

,

, .

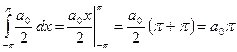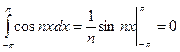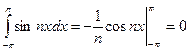Получаем:

.

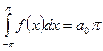
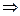
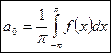Домножим равенство (3) на 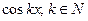и проинтегрируем по x от 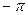до :

.

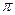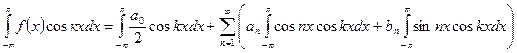Тогда .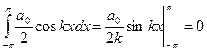

Если 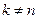, то

,

.

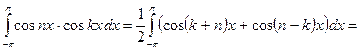
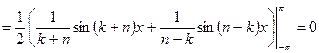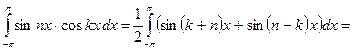
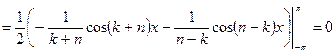Тогда при k = n получаем:

.

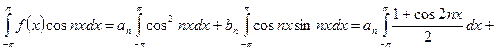
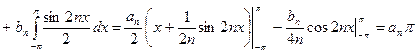Отсюда следует

.

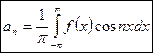Домножим равенство (3) на 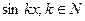и проинтегрируем по x от 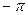до :

.

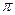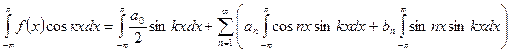
Тогда .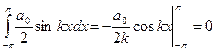

Если 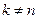, то

,

.

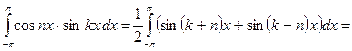
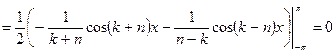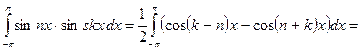
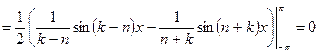Тогда при k = n:

.

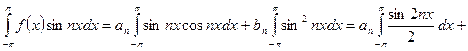
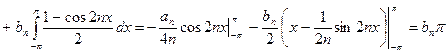Получаем

.

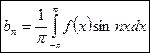Из определения ряда Фурье следует, что, для того чтобы найти ряд Фурье данной функции требуется найти коэффициенты Фурье этой функции и написать тригонометрический ряд с этими коэффициентами.

Сходимость ряда Фурье

Теорема Дирихле. Если функция f(x) на отрезке 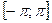имеет конечное число экстремумов и является непрерывной, за исключением, может быть, конечного числа точек разрыва I рода (т.е. удовлетворяет так называемым условиям Дирихле), то ряд Фурье в каждой точке отрезка 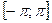сходится к функции f(x).

Если 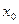- точка разрыва I рода функции f(x), то сумма ряда Фурье определяет функцию, совпадающую в точках непрерывности с функцией f(x) и равную 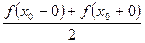в указанной точке разрыва I рода. За значение функции f(x) на каждой из границ отрезка 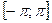будем принимать величину .

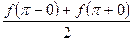Сумма ряда Фурье является периодической функцией с периодом .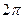

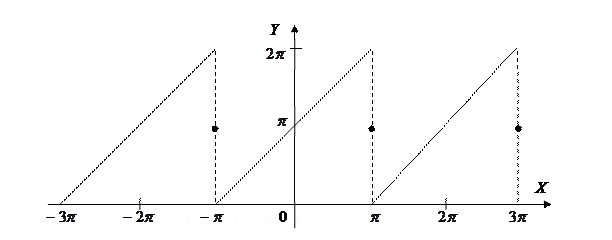
Пример. Разложить в ряд Фурье функцию, заданную на отрезке 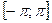уравнением .

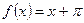Функция 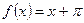удовлетворяет условиям Дирихле, сумма ряда Фурье функции 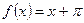является периодической функцией с периодом 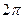и совпадает с функцией 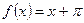на отрезке 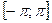. График суммы ряда Фурье приведён на рисунке.

Определяем коэффициенты ряда Фурье:

.

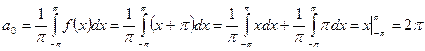Интеграл 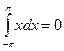, так как функция f(x)=x – нечётная.

.

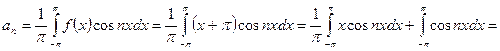
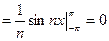Интеграл 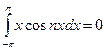, так как функция 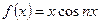– нечётная.

.

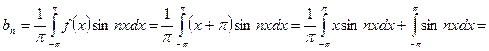
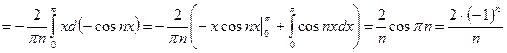Интеграл 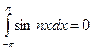, так как функция 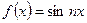– нечётная, интеграл 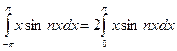, так как функция 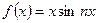– чётная. Интеграл 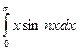вычисляем методом интегрирования по частям.

Разложение функции 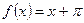в ряд Фурье имеет вид:

.

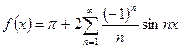Ряды Фурье для периодических функций с периодом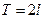

Если функция f(x) задана на отрезке [-l;l], где l – произвольное число, то при выполнении на отрезке [-l;l] условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье

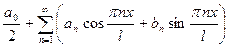
где

,

, .

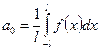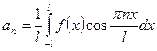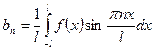Ряды Фурье для чётных и нечётных функций

Если f(x) - чётная функция, то получаем следующие коэффициенты Фурье:

, , .

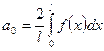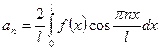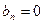Тогда ряд Фурье содержит только свободный член и косинусы, т.е.

.

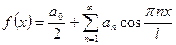Если f(x) - нечётная функция, то получаем:

, , .

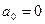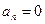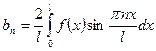Тогда ряд Фурье содержит только синусы, т.е.

.

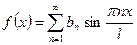Пример. Разложите в ряд Фурье функцию, заданную на отрезке [-1;1] уравнением .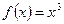

Функция 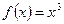удовлетворяет условиям Дирихле, сумма ряда Фурье функции 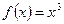является периодической функцией с периодом 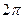и совпадает с функцией 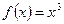на отрезке [-2;2].

Определяем коэффициенты ряда Фурье. Так как 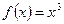- нечётная функция, то получаем:

, ,

.

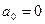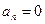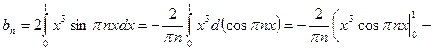
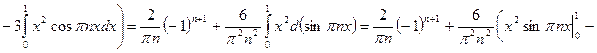
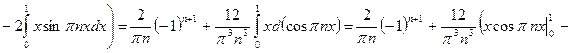
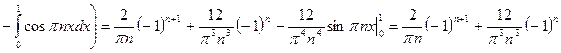Разложение функции 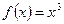в ряд Фурье имеет вид:

.

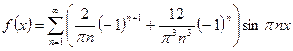РАЗДЕЛ 2. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

ЛЕКЦИЯ 5. КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Комплексные числа. Операции с комплексными числами

Для решения алгебраических уравнений множества действительных чисел R недостаточно (например, уравнения 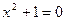и 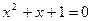не имеют действительных корней). Для преодоления указанного затруднения вводят множество комплексных чисел C ( 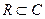). Решение уравнения 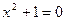обозначается через i и называется мнимой единицей, таким образом 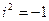, . Уравнение 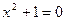имеет два комплексных корня .

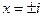Определение. Комплексным числом называется выражени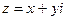е , где 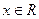, , 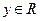i – символ мнимой единицы. Число x называется действительной частью, а число y - мнимой частью комплексного числа 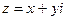. Два комплексных числа 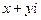и 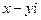, отличающиеся только знаком мнимой части, называются сопряжёнными.

Для комплексных чисел вводятся понятия равенства и операции сложения, вычитания, умножения и деления:

1) два комплексных числа 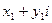и 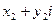равны тогда и только тогда, когда , ;

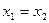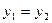2) комплексное число равно нулю 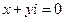тогда и только тогда, когда x=0, y=0;

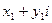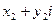3) суммой (разностью) чисел и называется число 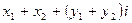(в случае разности );

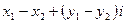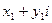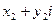4) произведением чисел и называется число ;

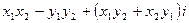5) деление комплексных чисел определяется как действие, обратное умножению: если 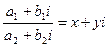, где 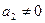, , 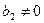то x и y должны быть такими, чтобы выполнялось равенство .

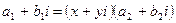Примеры. 1) Даны комплексные числа 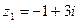, 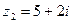. Найдите их сумму и разность.

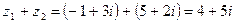
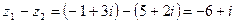
2) Даны комплексные числа