Спектральный анализ токов и напряжений выпрямителей
Наличие в выпрямителях нелинейных элементов (тиристоры, диоды), а так же значительных индуктивностей в нагрузке, вызывает появление несинусоидального тока в питающей сети. Выпрямленное напряжение имеет пульсации, зависящие от схемы выпрямления и глубины регулирования. Мощные выпрямители, как правило, на стороне постоянного тока имеют большие индуктивности, ими являются обмотки машин постоянного тока и сглаживающие реакторы. Индуктивности эти многократно превышают эквивалентную индуктивность стороны переменного тока, поэтому такие выпрямители по отношению к питающей сети переменного тока ведут себя как источники тока высших гармоник. Направляемый в сеть ток на частоте гармоники имеет величину, не зависящую от параметров питающей сети. Так как источники тока связаны с частотой сети, то они являются периодическими.
Из математики известно, что всякая периодическая функция 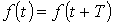 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверка на их выполнение не требуется..
При разложении в ряд Фурье функция может быть представлена в следующем виде: , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверка на их выполнение не требуется..
При разложении в ряд Фурье функция может быть представлена в следующем виде:
Здесь В выражении (1)
Коэффициенты ряда Фурье для стандартных функций могут быть взяты из справочной литературы или в общем случае рассчитаны по приведенным выше формулам. Однако в случае кривых, обладающих симметрией, задача существенно упрощается, поскольку из их разложения выпадают целые спектры гармоник. Знание свойств таких кривых позволяет существенно сэкономить время и ресурсы при вычислениях. Например:
В их разложении отсутствуют синусные составляющие, т.е.
К этому типу относятся кривые, удовлетворяющие равенству |
Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
- Максимальное значение -
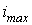 .
. - Действующее значение -
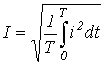 .
. - Среднее по модулю значение -
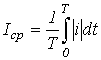 .
. - Среднее за период значение (постоянная составляющая) -
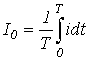 .
. - Коэффициент амплитуды (отношение максимального значения к действующему) -
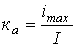 .
. - Коэффициент формы (отношение действующего значения к среднему по модулю) -
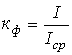 .
. - Коэффициент искажений (отношение действующего значения первой гармоники к действующему значению переменной) -
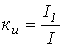 .
. - Коэффициент гармоник (отношение действующего значения высших гармонических к действующему значению первой гармоники) -
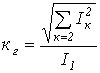 .
.
Свойства периодических кривых, обладающих симметрией
Как было показано выше, действующим называется среднеквадратичное за период значение величины. При наличии аналитического выражения функции i(t) и возможности взятия интеграла от ее квадрата действующее значение i(t) определяется точно. Однако в общем случае на практике действующее значение переменной определяется на основе информации о действующих значениях конечного ряда гармонических.
Пусть
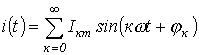 .
.
Тогда
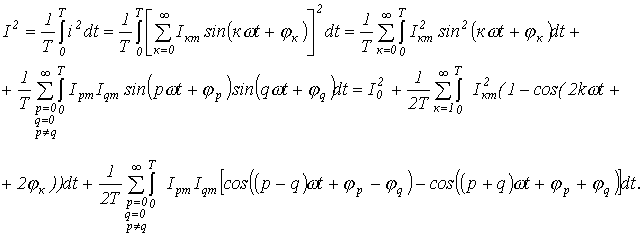
Очевидно, что каждый из интегралов от тригонометрических функций в последнем выражении равен нулю. Таким образом,
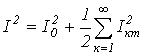
или
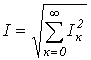 .
.
Аналогичные выражения имеют место для ЭДС, напряжения и т.д.
Мощность в цепях периодического несинусоидального тока
Пусть
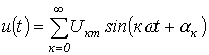 и
и 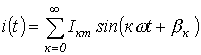 .
.
Тогда для активной мощности можно записать
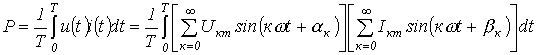 .
.
Как было показано при выводе соотношения для действующего значения несинусоидальной переменной, среднее за период значение произведения синусоидальных функций различной частоты равно нулю. Следовательно,
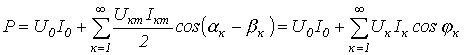 ,
,
где 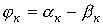 .
.
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармонических:
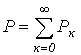 .
.
Аналогично для реактивной мощности можно записать
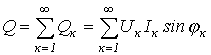 .
.
Полная мощность
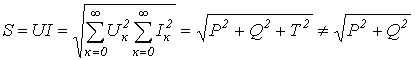 ,
,
где Т –мощность искажений,зависящая от степени отличия форм тока и напряжения.
Понятие об амплитудном и фазовом спектре сигнала
Простейшим периодическим (синусоидальным) сигналом является гармоническое колебание, которое можно записать в следующем виде:
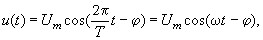
где 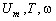 и
и 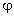 - амплитуда, период, частота и начальная фаза соответственно.
- амплитуда, период, частота и начальная фаза соответственно.
Пусть заданная в интервале 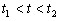 функция
функция 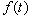 периодически повторяется с частотой
периодически повторяется с частотой 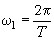 , где
, где 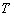 - период повторения, причём выполняются условия Дирихле:
- период повторения, причём выполняются условия Дирихле:
1. В любом конечном интервале функция 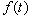 непрерывна или имеет конечное число разрывов первого рода;
непрерывна или имеет конечное число разрывов первого рода;
2. В пределах одного периода функция 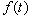 имеет конечное число максимумов и минимумов
имеет конечное число максимумов и минимумов
Ряд Фурье в тригонометрической форме запишем в следующем виде:
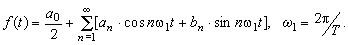 ……………… (2)
……………… (2)
Здесь 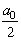 - среднее значение функции за период или постоянная составляющая, а
- среднее значение функции за период или постоянная составляющая, а 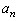 и
и 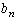 - амплитуды косинусоидальных и синусоидальных членов разложения
- амплитуды косинусоидальных и синусоидальных членов разложения  .
.
Эти величины определяются выражениями:
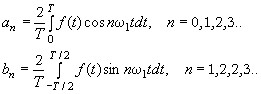 ……………. (3)
……………. (3)
Выражение (2) можно представить в виде суммы только косинусоид или только синусоид, но с различными фазами, например
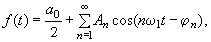 …………………….(4)
…………………….(4)
где амплитуда и фаза n-ой гармоники определяются выражениями
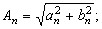 …………………………………………(5)
…………………………………………(5)
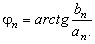 …………………………………………..(6)
…………………………………………..(6)
Совокупность значений 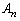 и
и 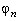 называется спектром функции
называется спектром функции 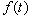 . График амплитудного спектра (5) изображён на рис. 1.
. График амплитудного спектра (5) изображён на рис. 1.
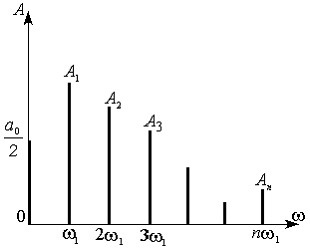
Рис 1. Графическое представление амплитудного спектра периодической функции.
Из выражения (5) и рис. 1 видно, что спектр периодической функции (сигнала) состоит из отдельных линий, отображающих в заданном масштабе амплитуды гармоник (5), соответствующих частотам 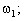
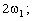
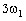 и т.д. Такой спектр называется линейчатым или дискретным.
и т.д. Такой спектр называется линейчатым или дискретным.
Для полной характеристики сигнала необходимо вычислить по формуле (6) фазу каждой гармоники и представить графически аналогично с амплитудным спектром, показанным на рис.1. Только по оси ординат в масштабе откладывают начальные фазы гармоник.
Дата добавления: 2017-09-01; просмотров: 1274;

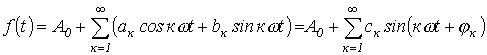 .
.
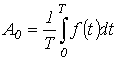 - постоянная составляющая или нулевая гармоника;
- постоянная составляющая или нулевая гармоника; 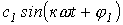 - первая (основная) гармоника, изменяющаяся с угловой частотой
- первая (основная) гармоника, изменяющаяся с угловой частотой 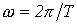 , где Т – период несинусоидальной периодической функции.
, где Т – период несинусоидальной периодической функции.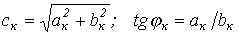 , где коэффициенты
, где коэффициенты 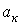 и
и 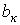 определяются по формулам
определяются по формулам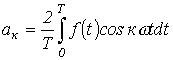 ;
;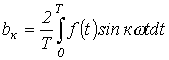
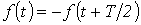 . В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е.
. В их разложении отсутствуют постоянная составляющая и четные гармоники, т.е. 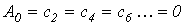 .
.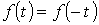 .
. 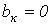 .
.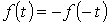 При разложении таких кривых отсутствуют постоянная составляющая (нулевая гармоника) и косинусные составляющие, т.е.
При разложении таких кривых отсутствуют постоянная составляющая (нулевая гармоника) и косинусные составляющие, т.е. 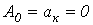 .
.








