Что такое Дисперсия

Для волновых процессов в реальных материальных средах характерно явление дисперсии. Проявляется оно в том, что локализованное начальное возмущение (волновое поле), распространяясь в пространстве, с течением времени претерпевает изменения, иногда довольно значительные. Рассмотрим, к примеру, цуг волн, генерируемый источником возмущений в фиксированной точке пространства в форме гармонического колебания заданной частоты, амплитуда которого отлична от нуля и постоянна в течение некоторого конечного интервала времени. Графически зависимость амплитуды исходного колебания от времени имеет форму прямоугольника. Если среда, в которой распространяется описанное возмущение, является диспергирующей средой, то с течением времени по мере удаления возмущения от места расположения источника колебаний описанный выше прямоугольник «расплывается», теряет первоначальный облик. В этих условиях возникают затруднения с определением скорости распространения возмущения и распознаванием сигнала. Человечеству повезло: звуковые волны распространяются в воздухе практически без дисперсии – человек пользуется голосом для передачи информации и способен её воспринимать; электромагнитные волны (включая световые) в разреженном пространстве и в воздухе обладают тем же свойством – человек может пользоваться радиосвязью и, главное, видеть окружающие предметы. Но не всегда так просто обстоит дело. Даже на самом простом и, казалось бы, изученном явлении преломления луча света на поверхности жидкости – это явление известно более двух тысяч лет, приходится учитывать явление дисперсии.

Плоская гармоническая волна, заполняющая всё пространство и существующая в течение неограниченного времени, имеет постоянную амплитуду, постоянную длину волны (волновое число), постоянное направление распространения, постоянную частоту колебаний (период колебаний). Совместное рассмотрение структуры волны и волнового уравнения в материальной среде приводит к дисперсионному уравнению: параметрической зависимости круговой частоты волны от волнового числа (волнового вектора). Дисперсионное уравнение позволяет вычислить фазовую скорость гармонической волны 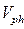и связать её с физическими параметрами среды. Явление дисперсии имеет место, если оказывается, что фазовая скорость гармонической волны 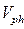зависит от круговой частоты (от длины или волнового числа) волны.

Для одиночных плоских гармонических волн явление дисперсии только тем и характерно, что фазовые скорости каждой из них в диспергирующей среде могут иметь различные значения. Сложнее дело обстоит с распространением сигнала (пакет гармонических волн) – совокупности гармонических волн различных частот и амплитуд в такой среде. Если поверхность равных фаз каждой составляющей сигнала распространяется с разной скоростью, то, естественно, начальная огибающая колебаний (форма сигнала) в произвольной точке пространства должна претерпевать искажение.

Помимо понятия «фазовая скорость»

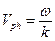, (1)

приходится вводить понятие «групповая скорость»

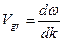(2)

для описания трансформации огибающей колебаний (формы сигнала) в процессе распространения волнового возмущения. Из определения фазовой и групповой скоростей непосредственно следуют зависимости, выявляющие влияние волнового числа или длины волны на величину различия групповой и фазовой скорости волны

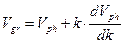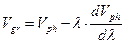, . (3)

Ещё раз подчеркнём, что явление дисперсии имеет место, если фазовая скорость волны зависит от волнового числа волны (частоты, или длины волны).

Явление дисперсии в поглощающей среде.

Рассмотрим одномерное линейное волновое уравнение с учётом эффектов поглощения:

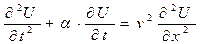. (4)

Здесь величина 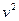является параметром, зависящим от свойств среды. Величина 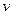имеет размерность скорости, в однородной среде эту величину принимаем постоянной. Физическое содержание величины 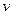, в частности, её связь со скоростью распространения волны выясним ниже. Параметр 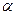, постоянный в рассматриваемом случае, характеризует интенсивность поглощения (для электромагнитной волны эта величина пропорциональна проводимости среды). Уравнение (4) возникает в теории распространения плоской электромагнитной волны в однородной изотропной среде с отличной от нуля электропроводностью. К этому же уравнению сводится и описание распространения поперечной волны в струне без изгибной жёсткости при условии, что колебания точек струны происходят в материальной среде, сила сопротивления при этом пропорциональна скорости точек струны. Заметим, что и параметр 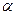, и параметр 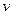в реальных условиях могут зависеть, в частности, от круговой частоты колебаний 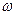. Ниже рассмотрена простейшая модель процесса распространения волны, позволяющая выявить характерные стороны явления.

Если в пространстве, заполненном рассматриваемой средой, распространяется плоская гармоническая волна

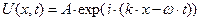, (5)

то, подставляя зависимость (5) в уравнение (4), приходим к дисперсионному уравнению:

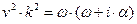. (6)

Из физических соображений решение дисперсионного уравнения запишем в виде:

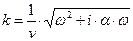. (7)

Выделим в зависимости (4) действительную и мнимую части:

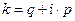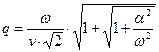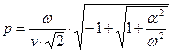, , . (8)

Асимптотические зависимости соотношений (8) при малых значениях параметра 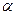имеют вид:

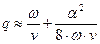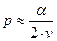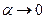, , . (9)

Плоская гармоническая волна с учётом соотношений (8) приобретает форму:

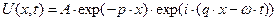. (10)

Величина р является параметром, описывающим изменение амплитуды колебаний с изменением координаты точки наблюдения, а величина q – параметром, входящим в определение мгновенной фазы колебаний в точке наблюдения. Поэтому в соответствии с определение фазовой скорости, получаем:

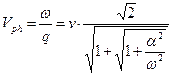. (11)

Характер зависимости (11) показан на рис.1.

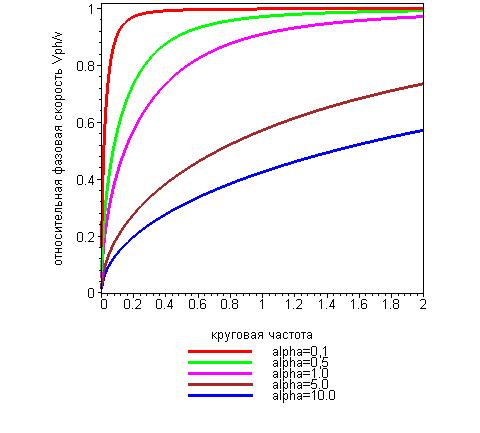
Рис.1. Зависимость безразмерной фазовой скорости волны

от круговой частоты 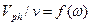для различных значений параметра .

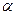Легко видеть, что фазовая скорость волны в рассматриваемом случае не совпадает с величиной параметра 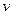и асимптотически стремится к этому пределу при больших значениях круговой частоты. Это различие особенно заметно для больших значений параметра 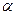, хотя характер зависимости фазовой скорости от круговой частоты сохраняется для всех значений параметра .

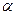Групповая скорость в рассматриваемом случае определяется выражением:

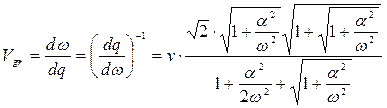. (12)

Графическая иллюстрация этой зависимости приведена на рис.2.

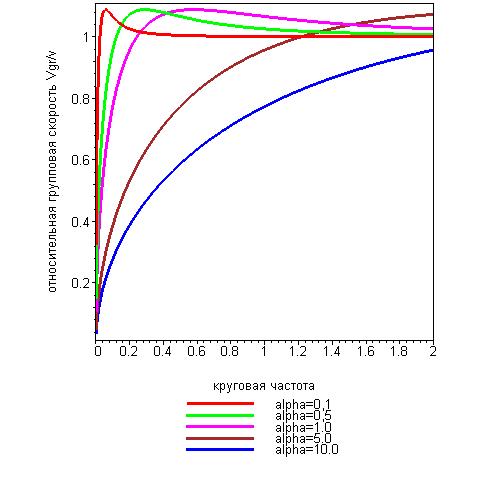
Рис.2. Зависимость безразмерной групповой скорости волны

от круговой частоты 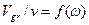для различных значений параметра .

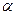Рассматривая рис.2, можно заметить, что существует интервал изменения круговой частоты, для которого групповая скорость волны имеет значения меньшее, чем значение параметра 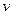, и интервал изменения круговой частоты, в котором групповая скорость больше, чем величина параметра 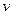. При больших значениях круговой частоты групповая скорость асимптотически стремится к пределу, равному значению параметра .

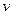Произведение фазовой скорости волны на групповую скорость оказывается равным

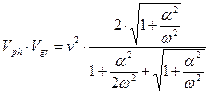. (13)

Характер изменения этого произведения с изменением круговой частоты показан на рис.3.

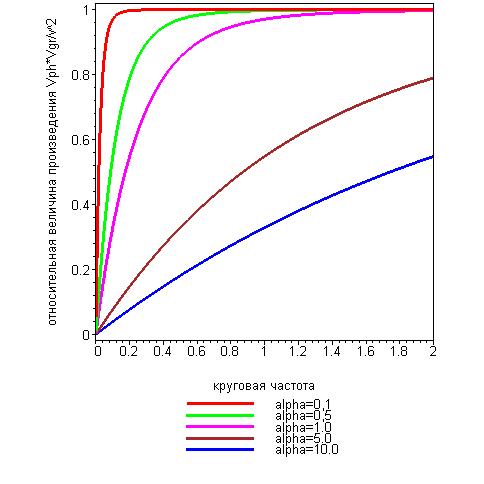
Рис.3. Зависимость безразмерного произведения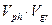

от круговой частоты 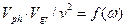для различных значений параметра .

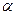Заметим, что соотношение

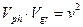(14)

имеет место только в случае 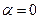, или, что эквивалентно, при условии , .

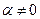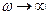Явление дисперсии в среде без поглощения.

Как правило, явление дисперсии связывают с наличием процессов поглощения. Однако это явление имеет место и в средах, в которых поглощение волны отсутствует.

Рассмотрим одномерную форму волнового процесса произвольной физической природы в линейной диспергирующей среде:

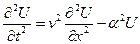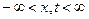, . (15)

Уравнение (15), в частности, описывает поперечные колебания однородной струны без изгибной жёсткости в упругой среде, в этом случае на элемент струны действует дополнительная возвращающая сила, пропорциональная смещению рассматриваемого элемента струны.

В уравнении (15) предполагаем, что выполнены условия 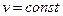и 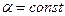, при этом необходимо сделать оговорку, что величина 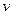характеризует динамические свойства системы с распределёнными параметрами и, хотя и имеет размерность скорости, не является в общем случае фазовой скоростью гармонической волны.

Предполагаем, что решение волнового уравнения (15) можно записать в виде: 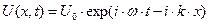. (16)

Здесь амплитуда, круговая частота и волновое число гармонической волны определены соотношениями:

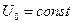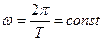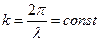, , . (17)

В результате использования зависимости (16) в уравнении (15) с учётом соотношений (17) приходим к дисперсионному уравнению:

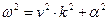. (18)

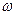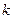Заметим, что форма волнового уравнения (4) была выбрана специальным образом: дисперсионное уравнение (18) можно изучать в действительной области изменения и - параметров задачи.

Разделим левую и правую части уравнения (18) на величину :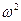

.

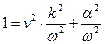Полученное соотношение в соответствии с определением фазовой скорости гармонической волны можно переписать в форме:

.

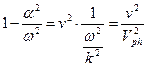В итоге получаем зависимость фазовой скорости волны от круговой частоты 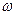и свойств среды, в которой эта волна распространяется:

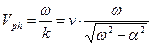. (19)

Привлекательность соотношения (19) для формирования физических представлений о явлении дисперсии состоит в том, что в нём явно выражена зависимость фазовой скорости от круговой частоты 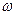и наглядно видно различие физических величин 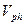и .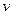

Переписывая дисперсионное уравнение (18) «в дифференциалах», получим:

,

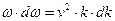поскольку параметр 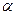в рассматриваемой модели явления считается постоянной величиной. Теперь несложно получить соотношение:

.

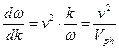Вычислим групповую скорость гармонической волны в соответствии с её определением

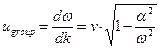. (20)

На рис.4 приведена графическая иллюстрация зависимостей фазовой и групповой скорости волны в рассматриваемой среде от круговой частоты при некоторых заданных значениях параметра .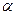

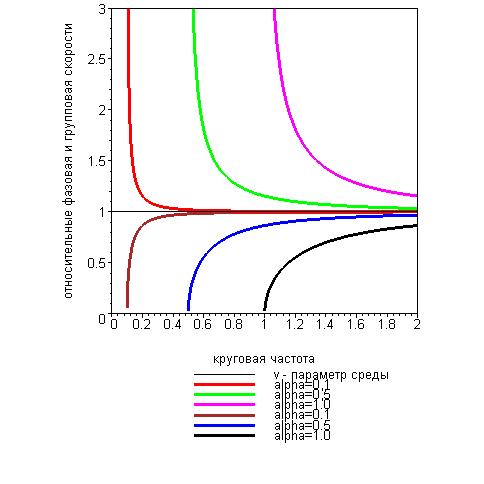
Рис. 4. Зависимости безразмерных величин фазовой 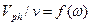и групповой 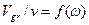скоростей от круговой частоты 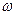. (верхние кривые – фазовая скорость, нижние – групповая)

Заметим, что фазовая и групповая скорости гармонической волны в диспергирующей не поглощающей среде не совпадают между собой. В отсутствие явления дисперсии фазовая и групповая скорости гармонической волны не зависят от круговой частоты и совпадают с величиной 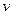. В рассматриваемом случае это возможно при выполнении условия 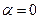. Если выполнено условие 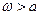, имеют место зависимости:

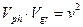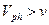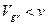, , , (21)

Из соотношения (21) следует, что групповая и фазовая скорости волны специфическим образом связаны между собой.

Современные физические представления не накладывают ограничений на величину фазовой скорости гармонической волны, она может быть и меньше и больше скорости света в вакууме. Относительно групповой скорости говорят, что она должна быть меньше скорости света в вакууме, поскольку никакой сигнал быстрее скорости света в вакууме распространяться не может.