Теорема Гаусса для электростатического поля в вакууме.

Вектор напряженности электростатического поля 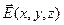в силу своей физической природы обладает двумя специфическими свойствами. Первое из них вскрывает связь пространственного расположения неподвижных электрических зарядов, создающих вокруг себя электростатическое поле, с некоторыми интегральными и дифференциальными выражениями для вектора напряженности электростатического поля. Второе свойство является следствием закона Кулона, согласно которому силы электростатического взаимодействия являются центральными, а это обуславливает потенциальный характер электростатического поля. Настоящий раздел посвящен обсуждению первого, а следующий – второго свойства электростатического поля.

2.3.1. Поток вектора.

Пусть в некоторой области пространства известен вектор напряженности электростатического поля 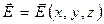. Допустим, что в окрестности произвольной фиксированной точки пространства имеется элемент поверхности площади 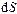, ориентацию которого можно задать с помощью вектора единичной (безразмерной) нормали 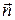к этому элементу поверхности. Поскольку элемент поверхности является двусторонним объектом, то направление нормали можно выбрать произвольно. Введем в рассмотрение объект

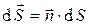, (1)

- вектор элемента площади поверхности (рис.1).

В соответствии с определением (1) этот вектор численно равен площади элемента поверхности, имеет размерность площади и направлен вдоль 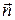, то есть вдоль нормали к элементу поверхности.

Элементарный поток 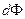вектора 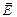через площадку 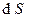по определению равен скалярному произведению векторов 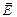и :

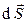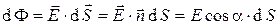. (2)

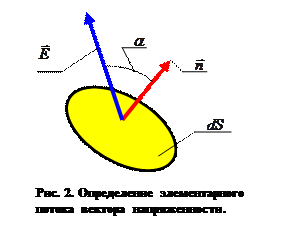
Угол 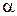в выражении (2) измеряется между направлением вектора 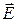и направлением нормали 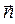к площадке 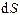(рис.2).

При 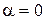, то есть при 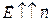, значение элементарного потока вектора максимально, а при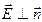 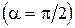элементарный поток обращается в нуль. Это свойство элементарного потока легко понять, если привлечь понятие силовой линии векторного поля. В первом случае силовые линии перпендикулярны площадке 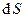, а во втором случае они “скользят” вдоль площадки, не пересекая ее. Заметим, что 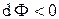, если угол 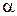- тупой.

Если рассматривать поверхность конечных (или бесконечных) размеров, то можно определить поток вектора 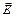через эту поверхность как алгебраическую сумму элементарных потоков вектора 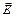через ориентированные в пространстве элементы поверхности :

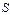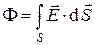. (3)

В определении (3) подразумевается, что поверхность 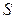достаточно гладкая, направления нормалей к двум соседним элементам поверхности не сильно различаются между собой. Последнее означает, что все элементы поверхности 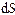построены “на одной стороне” поверхности 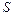. В случае бесконечных размеров поверхности 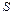, а иногда и для поверхности конечных размеров, встает вопрос о существовании интеграла (3). Если поверхность 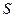является замкнутой поверхностью, то, как правило, поток вектора через поверхность 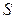рассчитывают с использованием внешней нормали по отношению к объему, заключенному внутри поверхности :

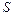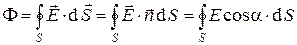, (4)

где кружок у интеграла означает, что поверхность 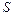- замкнутая. Приведенное выше определение можно записать в форме

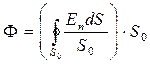. (5)

Здесь индекс «ноль» у символа 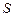введён только для того, чтобы подчеркнуть, что величина площади поверхности 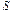в знаменателе подынтегрального выражения является неизменяемой величиной. В этом случае абстрактное определение потока вектора через поверхность 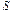можно наполнить следующим содержанием: