Оценки сложности алгоритмов дискретной оптимизации

Проблема оценки сложности алгоритмов и задач оптимизации в зависимости от размерности задачи представляет большой теоретический и практический интерес и позволяет получить представление о трудоемкости решения задач дискретной оптимизации.

Введем оценку сложности алгоритма ДО[9]. Известно, что множество решений задачи 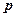булева программирования образует множество вершин n–мерного единичного куба 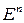. Пусть 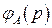– число просмотренных вершин куба 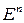после того, как индивидуальная задача ДО 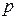решена с помощью алгоритма .

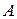Определение 5.18.Оценкой эффективности (сложностью) алго­ритма 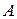на классе задач 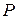называется величина

.

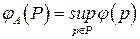Таким образом, введенная оценка сложности является оценкой «в худшем случае», в дальнейшем вычислительную временну́ю сложность алгоритмов ДО будем называть оценкой эффективности алгоритмов.

Отметим некоторые результаты теории сложности в ДО.

В [10] показано, что для задач целочисленного линейного прог­раммирования с булевыми переменными, таких, что

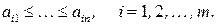
ОЭ аддитивного алгоритма Балаша имеет следующий вид:

.

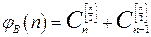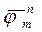В [11] анализируется другая оценка сложности алгоритма Балаша – среднее число итераций, причем получено, что оценка среднего числа итераций алгоритма Балаша решения задач ЦЛП с 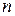булевыми переменными и 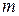ограничениями:

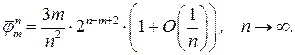
Эффективность алгоритма ветвей и границ при решении задач дискретного программирования оценивается числом решенных подзадач, т.е. числом вершин в дереве ветвления. Приведем без доказательства пример плохой (патологической) задачи, построенный Ю.Ю. Финкельштейном[12], в которой число вершин дерева ветвления несущественно отличается от :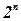

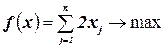
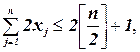
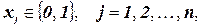
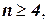
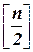‑ целая часть от .

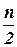Конструкция примера проста. Все множество оптимальных решений состоит из всех булевых векторов 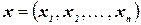, содержащих 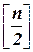единиц и 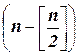нулей. Для точного решения задачи применяется алгоритм Ленд и Дойг.

Теорема 5.5. Для числа 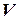вершин дерева ветвления имеет место равенство

.

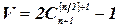Используя формулу Стирлинга, получим следующее асимптотическое равенство:

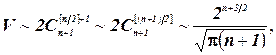
т.е. 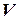несущественно отличается от оценки полного перебора, равной .

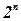[1] Алан М. Тьюринг ‑ английский математик.

[2] Таким алфавитом может быть двоичный алфавит или набор символов ASCII.

[3] Такой набор называется выполняющим.

[4] Хачиян Л. Г. Полиномиальный алгоритм в линейном программировании // Докл. АН СССР. — 1979. — Т. 244, № 5. — С. 1093-1096.

[5] Karmarkar N. A new polynomial-time algorithm for linear programming // Combinatorica. – 1984. ‑ №4. – P. .373–395.

[6] Михалевич В.С., Кукса А.И. Методы последовательной оптимизации. ‑ М.: Наука, 1983. ‑ 205 с.

[7] Klee V., Minty G.J. How good is the simplex algorithm? // Inequalities, III / O. Shisha (ed.). ‑ New York: Academic Press, 1972. ‑ P. 159-175.

[8] Dempe S. Worst-case and average-case analysis of an algorithm solving a generalized knapsack problem // Mathematische Operationsforschung und Statistik. ‑ 1983. ‑ V. 14. ‑ P. 551-564.

[9] Гришухин В.П. Алгоритмы ветвей и границ в задачах с булевыми переменными, оценка их эффективности // Экономика и математические методы. ‑ 1976. ‑ 12, № 4. ‑ С. 757-766.

[10] Гришухин В.П. Оценка сложности алгоритма Балаша // Математические методы решения экономических задач. ‑ М.: Наука. ‑ 1972. ‑ Вып.3. ‑ С. 93-105.

[11] Гришухин В.П. О среднем числе итераций алгоритма Балаша // Исследования по дискретной математике. ‑ М.: Наука. ‑ 1973. ‑ С. 58-68.

[12] Финкелъштейн Ю. Ю. Приближенные методы и прикладные задачи дискретного программирования. — М.: Наука, ‑ 1976.