Схема триггера на биполярных транзисторах

Состоит из двух ключей на транзисторах, между которыми организо-

ваны положительные обратные связи. Схема имеет два устойчивых состоя-

ния: на выходе есть напряжение (одно состояние), на выходе нет напряжения (другое состояние). Переход из одного состояния в другое осуществля-

ется под действием управляющих импульсов. После изменения состояния

на противоположное управляющие сигналы могут отсутствовать. Сохране-

ние состояния при этом обеспечивается за счёт положительных обратных

связей. Схема представлена на рис.158. При нарисовании триггерной схе-

мы сначала рисуются два ключа и добавляются обратные связи. Обратная связь-это связь с выхода на вход.

Работа схемы. Пусть VT₂ закрыт. Под действием напряжения на его коллекторе через R_б3 протекает ток, удерживающий VT₁ в открытом состоянии. В то же время открытый VT₁ закорачивает базовую цепь транзистора VT₂ с резистором R_б4. Закрытое состояние VT₂ соответствует значению выхода Q=1. Открытое состояние VT₁ - 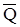=0. Напряжение на коллекторе закрытого транзистора (Q=1) равно:

U_Q=Uп×R_б3/(R_К2+R_б3) .

Для того, чтобы сменить состояние триггера на противоположное, необходимо подать сигналы на вход R или S. Входные сигналы обычно являются импульсными. Наличие напряжения на входе S (S=1) устанавливает Q=1, а наличие напряжения на входе R (R=1) устанавливает Q=0. Одновременная подача сигнала на входы S и R запрещена, т.к. триггер при этом перестаёт быть триггером (не будет противоположного состояния Q и ).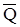

Диаграммы работы при наличии входных импульсных сигналов показаны на рис. 159. На интервале между импульсами на входах S и R триггер помнит то состояние, в которое он был установлен по этим входам, т.е. триггер - элемент памяти.

Расчет элементов схемы. Триггер в большинстве случаев является симметричной схемой, поэтому R_к1=R_к2, R_б3=R_б4 и можно рассчитывать половинку триггера. Уравнения для расчета:

I_б=I_к/(1,5¸2) h_21э,

где (1.5¸2) -коэффициент насыщения;

I_к=Uп/R_к.

Сопротивления R_к1 и R_к2 обычно заданы, поэтому I_к известен, тогда

R_б=U_Q/I_б.

Выражение для U_Q -смотри выше.