Если рассматриваются совместные события, вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности совместного их наступления.
Символически это записывается следующей формулой:
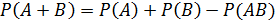
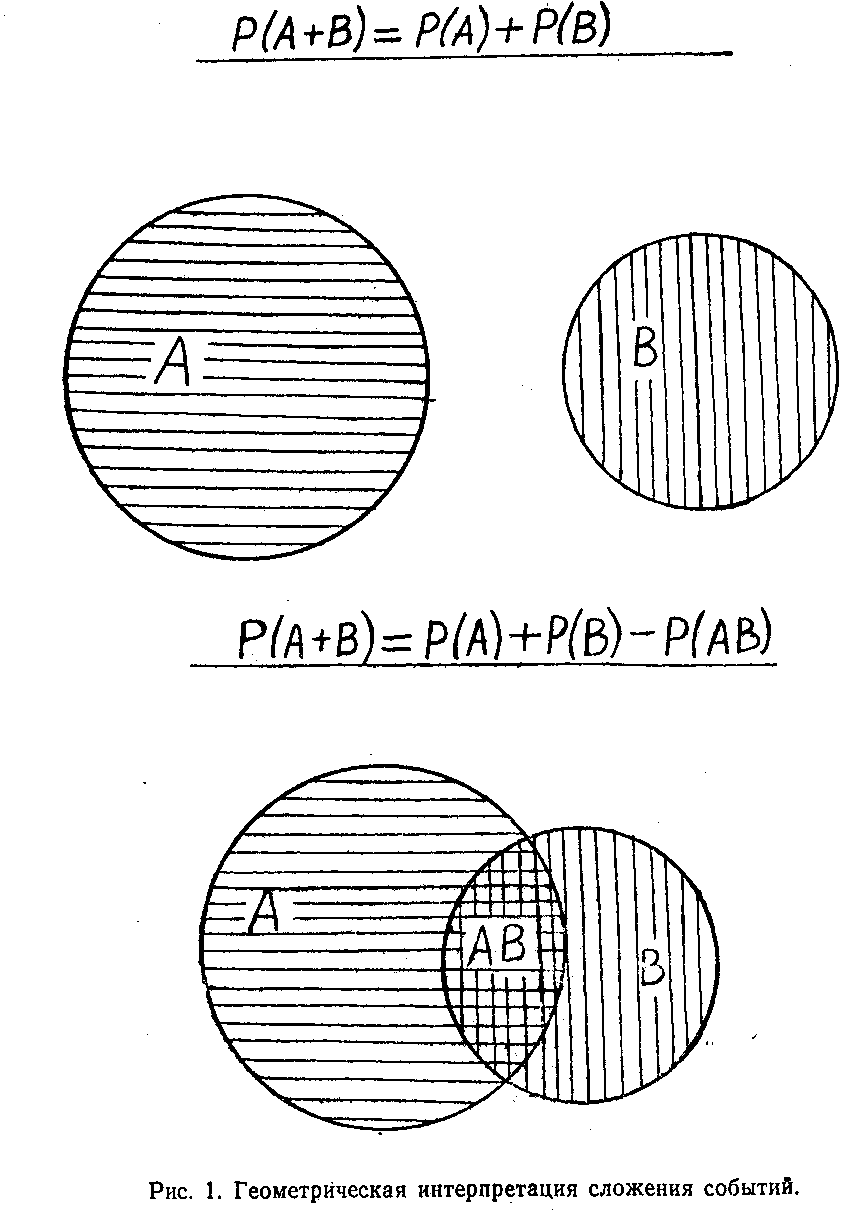
Если представить себе, что событие А заключается в попадании при стрельбе в мишень, заштрихованную горизонтальными полосами, а событие В — в попадании в мишень, заштрихованную вертикальными полосами, то в случае несовместных событий по теореме сложения вероятность суммы равна сумме вероятностей отдельных событий. Если же эти события совместны, то есть некоторая вероятность, соответствующая совместному наступлению событий А и В. Если не ввести поправку на вычитаемое Р(АВ), т.е. на вероятность совместного наступления событий, то эта вероятность будет учтена дважды, так как площадь, заштрихованная и горизонтальными, и вертикальными линиями, является составной частью обеих мишеней и будет учитываться как в первом, так и во втором слагаемом.
На рис. 1 дана геометрическая интерпретация, наглядно иллюстрирующая данное обстоятельство. В верхней части рисунка помещены непересекающиеся мишени, являющиеся аналогом несовместных событий, в нижней части — пересекающиеся мишени, являющиеся аналогом совместных событий (одним выстрелом можно попасть сразу и в мишень А, и в мишень В).
|
Прежде чем перейти к теореме умножения, необходимо рассмотреть понятия независимых и зависимых событий и условной и безусловной вероятностей.
Независимым от события В называется такое событие А, вероятность появления которого не зависит от появления или непоявления события В.
Зависимым от события В называется такое событие А, вероятность появления которого зависит от появления или непоявления события В.
Пример. В урне находятся 3 шара, 2 белых и 1 черный. При выборе шара наугад вероятность выбрать белый шар (событие А) равна: Р(А) = 2/3, а черный (событие В)Р(В) = 1/3. Мы имеем дело со схемой случаев, и вероятности событий рассчитываются строго по формуле. При повторении опыта вероятности появления событий А и В остаются неизменными, если после каждого выбора шар возвращается в урну. В этом случае события А и В являются независимыми. Если же выбранный в первом опыте шар в урну не возвращается, то вероятность события (А) во втором опыте зависит от появления или непоявления события (В) в первом опыте. Так, если в первом опыте появилось событие В (выбран черный шар), то второй опыт проводится при наличии в урне 2 белых шаров и вероятность появления события А во втором опыте равна: Р(А) = 2/2= 1.
Если же в первом опыте не появилось событие В(выбран белый шар), то второй опыт проводится при наличии в урне одного белого и одного черного шаров и вероятность появления события А во втором опыте равна: Р(А)=1/2. Очевидно, в этом случае события А и В тесно связаны и вероятности их появления являются зависимыми.
Условной вероятностью события А называется вероятность его появления при условии, что появилось событие В. Условная вероятность символически обозначается Р(А/В).
Если вероятность появления события А не зависит от появления события В, то условная вероятность события А равна безусловной вероятности:
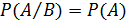
Если вероятность появления события А зависит от появления события В, то условная вероятность никогда не может быть равна безусловной вероятности:
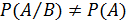
Выявление зависимости различных событий между собой имеет большое значение в решении практических задач. Так, например, ошибочное предположение о независимости появления некоторых симптомов при диагностике пороков сердца по вероятностной методике, разработанной в Институте сердечно-сосудистой хирургии им. А. Н. Бакулева, обусловило около 50% ошибочных диагнозов.
Теорема умножения
Вероятность произведения двух событий А и В равна произведению вероятности одного из них (А) на условную вероятность другого (В), вычисленную при условии, что первое имело место.
Символически это записывается следующим образом:
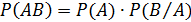
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Следствие 2. Вероятность произведения независимых событий равна произведению вероятностей этих событий.
Как уже говорилось, под произведением событий понимается совместное их появление.
Для двух событий по теореме умножения имеем:

Но поскольку события независимы, справедливо равенство Р(В/А) = Р(В), и тогда получаем: 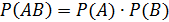
Для трех событий по аналогии получаем: 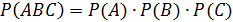
Пример. Из урны, в которой находятся 1 черный и 2 белых шара ( 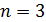 ), выбираем два шара подряд. Какова вероятность того, что оба шара белые?
), выбираем два шара подряд. Какова вероятность того, что оба шара белые?
Решение. Обозначим интересующее нас событие через А, а события, заключающиеся в выборе белого шара первый и второй раз — через A1 и А2, соответственно. Интересующее нас событие равно произведению событий A1 и А2: 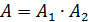 .
.
По теореме умножения имеем: 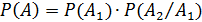 .
.
Так как всего шаров три и из них два белых, то 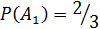 .
.
Так как после появления события 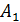 (после выбора белого шара первый раз) осталось всего два шара, из них белых – один, то
(после выбора белого шара первый раз) осталось всего два шара, из них белых – один, то 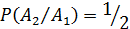 .
.
Тогда:
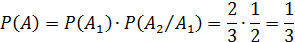
Если после выбора белого шара первый раз его возвращают в урну, то события 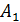 и
и 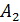 будут независимыми и равными:
будут независимыми и равными:
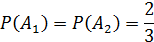
Тогда искомая вероятность будет равна:
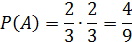
Дата добавления: 2016-06-05; просмотров: 2380;











