Подход и модели для получения параметрических ограничений

Получение параметрических ограничений в условиях неопределенности для динамических систем

Учет параметрических ограничений в задачах идентификации неразрывно связан с проблемой робастности. Обычно при синтезе адаптивных систем используются параметрические ограничения, полученные на основе анализа априорной информации. Такой же подход применяется при задании ограничений на структурные возмущения в системе. В условиях априорной неопределенности такая информация, как правило, отсутствует. Проблеме получения апостериорных параметрических ограничений в условиях неопределенности уделялось большое внимание в работах по гарантированному оцениванию, исходя из информации о возмущениях. Нами предложен метод синтеза моделей для оценки параметрических ограничений в условиях неопределенности на основе нахождения мажорирующих решений для динамической системы, который в отличие от не требует данных о неконтролируемых возмущениях.

Ниже рассматривается задача формирования параметрических ограничений и ограничений на неопределенность для непрерывной нестационарной динамической системы с обобщенным входом на основе адаптивного подхода и нахождения мажорирующих решений для динамической системы.

Постановка задачи

Рассматривается непрерывная динамическая система, описываемая в пространстве “вход-выход” системой уравнений

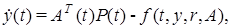(1)

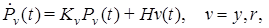(2)

где 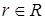, 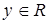— вход и выход системы; 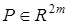— обобщенный вход, 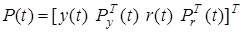, , 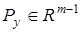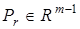; 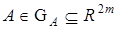— вектор параметров, принадлежащий ограниченной, но априори неизвестная области 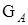; 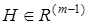— известный вектор; 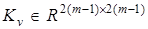— гурвицева матрица; 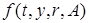— неопределенность. Пара 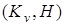является управляемой.

Предполагается, что при 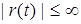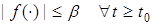, где 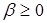. Передаточная функция системы (1), (2) является положительной действительной.

Введение обобщенного входа 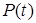(его еще называют регрессионным) связано с приведением динамической системы 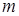-го порядка к идентификационной форме (неминимальная реализация) относительно выхода 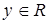. 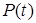включает в себя как сам вход 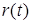, так и выход системы 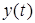и их преобразования 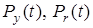, полученные в результате пропускания 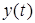и 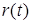через систему (2). Отсюда название вектора .

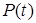Для системы (1), (2) известна информация

,

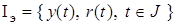где 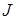— интервал наблюдения.

Ставится задача: на основе анализа данных 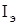о функционировании системы (1), (2) найти оценки для области 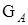и верхнюю границу для числа .

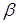Подход и модели для получения параметрических ограничений

Решение уравнения (1) имеет вид

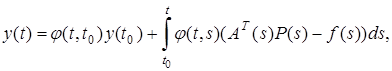(3)

где 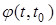— переходная функция. Дискретный аналог уравнения (3):

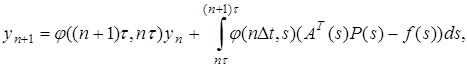(4)

где 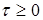— интервал дискретизации, 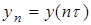. Из (4) получаем оценку

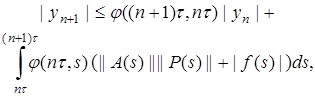(5)

где 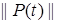— норма вектора 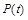в соответствующем пространстве.

Неравенство (5) давно известно и широко применяется в теоретических исследованиях. Одним из достоинств оценки (5) является то, что она связывает между собой элементы множества 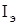, вектор 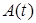и неопределенность 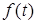. Поэтому в дальнейшем область 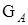будем представлять в виде

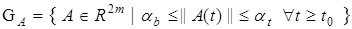, (6)

где 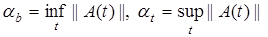являются границами области 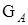. Из допущений, сделанных в §1.1 относительно системы (1), (2), следует, что .

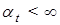Неравенство (5) затруднительно применять для идентификации границ области 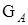. Поставим в соответствие (5) некоторое уравнение, которое позволяло бы использовать элементы множества 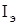или их преобразования. Воспользуемся идеей мажорирующих уравнений (верхних и нижних), которые применяются в теории устойчивости для построения систем сравнения.

Прежде чем приводить мажорирующие уравнения, получим множество 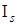на основе преобразования элементов множества 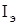. Для каждого 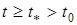будем определять функции

.

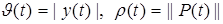В результате получим множество 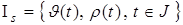. Выделим в 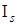два подмножества

,

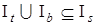где 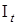содержит “верхнее” значение функции 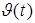и соответствующие им 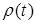для заданного 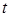, 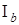— “нижние” значения, .

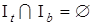Для классификации множества 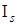на два подмножества 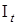и 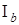введем некоторое число (порог) 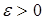, которое можно выбирать как на основе анализа априорной информации, так и определять в результате обработки множества 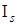(в условиях неопределенности). Тогда алгоритм формирования множеств 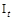, 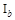примет вид

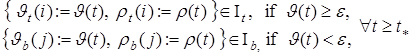, (7)

где 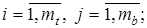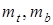— соответственно мощность множеств 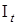, 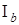; 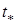— момент начала классификации функций 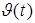, 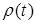; := — знак присвоения.

Из процедуры (7) следует, что 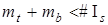, где 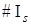— мощность множества 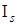, что и отражает (7).

Предположим, что 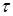является достаточно малым и 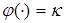, 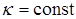. Тогда верхнее решение (T-решение) неравенства (7) с учетом (6) и (7) запишем в виде

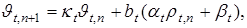(8)

где 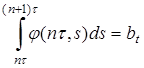. Аналогично получаем нижнее решение:

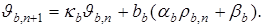(9)

В дальнейшем для удобства ссылки (8) и (9) будем соответственно называть T- и B-системой.

Итак, задача получения параметрических ограничений 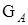для (1), (2) сведена к оценке параметров T-и B-системы. Прежде, чем переходить к синтезу адаптивных алгоритмов, опишем процедуру получения порога. Изложенная процедура реализует алгоритмы адаптивного интервального оценивания.