Регрессионные и авторегрессионные модели
СИНТЕЗ РЕГРЕССИОННЫХ МОДЕЛЕЙ
Основные понятия и определения
Регрессионный анализ относят к классическим статистическим методам. Благодаря своим широким возможностям различные регрессионные процедуры давно и успешно используются в инженерной практике для идентификации процессов, однако их применение к идентификации многомерных процессов в реальном масштабе времени стало возможным только с развитием и внедрением быстродействующих компьютеров.
Методы идентификации, основанные на регрессионных процедурах с использованием метода наименьших квадратов, применимы как к линейным, так и к нелинейным процессам и облегчают проведение идентификации по нескольким входам одновременно. Более того, регрессионные методы позволяют осуществлять идентификацию в реальном масштабе времени, поскольку они основаны на измерениях входных и выходных сигналов, которые можно получить в процессе нормального функционирования системы.
Термин "регрессия" был введён Френсисом Гальтоном в конце 19-го века. Гальтон обнаружил, что дети родителей с высоким или низким ростом обычно не наследуют выдающийся рост и назвал этот феномен "регрессия к посредственности". Сначала этот термин использовался исключительно в биологическом смысле. После работ Карла Пирсона этот термин стали использовать и в статистике.
В статистической литературе различают регрессию с участием одной свободной переменной (входом системы) и с несколькими свободными переменными (вектор входа) — парную и многомерную регрессию. Различают линейную и нелинейную регрессию. Если регрессионную модель не является линейной комбинацией функций от параметров, то говорят о нелинейной регрессии. При этом модель может быть произвольной суперпозицией функций из некоторого набора. Нелинейными моделями являются, экспоненциальные, тригонометрические и другие, полагающие зависимость между параметрами и зависимой переменной нелинейной.
Различают параметрическую и непараметрическую регрессию. Строгую границу между этими двумя типами регрессий провести сложно. Сейчас не существует общепринятого критерия отличия одного типа моделей от другого. Например, считается, что линейные модели являются параметрическими, а модели, включающие усреднение зависимой переменной по пространству свободной переменной —непараметрическими. Пример параметрической регрессионной модели: линейный предиктор, многослойный персептрон. Примеры смешанной регрессионной модели: функции радиального базиса. Непараметрическая модель — скользящее усреднение в окне некоторой ширины. В целом, непараметрическая регрессия отличается от параметрической тем, что зависимая переменная зависит не от одного значения свободной переменной, а от некоторой заданной окрестности этого значения.
Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть 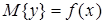 , где , где 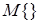 — знак математического ожидания. — знак математического ожидания.
|
Регрессионный анализ сводится к поиску такой функции 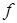 , которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих
, которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих
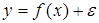
где 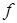 — функция регрессионной зависимости, а e — аддитивная случайная величина. Предположение о характере распределения этой величины называется гипотезой порождения данных. Обычно предполагается, что величина e имеет гауссово распределение с нулевым средним и дисперсией
— функция регрессионной зависимости, а e — аддитивная случайная величина. Предположение о характере распределения этой величины называется гипотезой порождения данных. Обычно предполагается, что величина e имеет гауссово распределение с нулевым средним и дисперсией 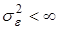 .
.
Регрессионные и авторегрессионные модели
Для описания систем могут применяться статические (описываются системой алгебраических уравнений) и динамические регрессионные уравнения.
Для системы с одним выходом регрессионное линейное относительно параметров уравнение имеет вид (Р-модель)
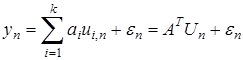 , (1)
, (1)
где 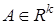 — вектор параметров,
— вектор параметров, 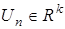 — вектор входа,
— вектор входа, 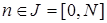 — дискретное время.
— дискретное время.
Из (1) при 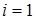 получаем парную регрессию, при
получаем парную регрессию, при 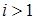 (1) описывает множественную регрессию.
(1) описывает множественную регрессию.
Для описания динамических процессов применяется обобщение (1), имеющее АР часть
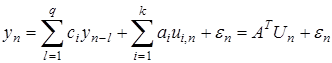 . (2)
. (2)
(1) и (2) могут содержать некоторые нелинейные составляющие и им соответствует нелинейная регрессия.
Дата добавления: 2017-02-13; просмотров: 2766;











