Расчет балок из хрупких материалов
Хрупкие; материалы применяют для изготовления некоторых работающих на изгиб элементов машиностроительных конструкций. В частности, из серого чугуна отливают различного рода рамы, станины, подшипниковые подвески и т. и. Как известно, серый чугун работает на сжатие значительно лучше, чем на растяжение; отношение соответствующих допускаемых напряжений
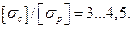
Очевидно, применение сечения, симметричных относительно нейтральной оси, в рассматриваемом случае нерационально - материал в сжатой зоне бруса будет значительно недогружен, что приведет к его излишней затрате, а значит, к увеличению массы конструкции.
Для балок из хрупких материалов, различно сопротивляющихся растяжению и сжатию, целесообразно применять сечения, не симметричные относительно нейтральной оси, например тавровое, несимметричное двутавровое, П-образное. При этом целесообразно располагать сечение таким образом, чтобы большая часть балки находилась в растянутой зоне, при этом растянутые волокла оказываются приближенными к центру тяжести сечения.
Очевидно, следует стремиться к тому, чтобы максимальные растягивающие и максимальные сжимающие напряжения в опасном поперечном сечении балки были одновременно равны соответствующим допускаемым напряжениям, .т. е.
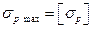 ;
; 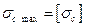 .
.
При этом материал балки используется наиболее рационально. Но
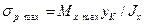 и
и 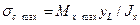
где 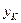 и
и 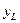 - расстояния от нейтральной оси соответственно до наиболее удаленных дочек растянутой и сжатой зон сечения. Следовательно, для обеспечения указанного условия наиболее рационального использования материала сечение должно иметь такую конфигурацию, при которой
- расстояния от нейтральной оси соответственно до наиболее удаленных дочек растянутой и сжатой зон сечения. Следовательно, для обеспечения указанного условия наиболее рационального использования материала сечение должно иметь такую конфигурацию, при которой
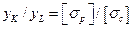 .
.
Полученное соотношение выполняется далеко не всегда, поэтому условие прочности чугунной балки выражается двумя неравенствами:
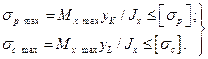
Задача.
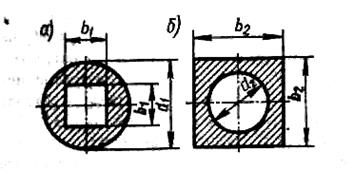
Две балки с поперечными сечениями, показанными на рисунке, нагружены вертикально направленной изгибающей нагрузкой. Выяснить, как изменится допускаемая нагрузка для каждой из балок при повороте их вокруг продольных осей на 450.
Решение.
Из формулы 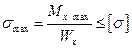 следует, что допускаемое значение максимального изгибающего момента определяется по зависимости
следует, что допускаемое значение максимального изгибающего момента определяется по зависимости
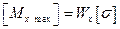
т. е. при заданном значении допускаемого напряжения допускаемый изгибающий момент зависит только от момента сопротивления поперечного сечения балки. Для обоих заданных сечений любая центральная ось - главная, поэтому при повороте балки (сечения) момент инерции относительно нейтральной оси остается постоянным.
Для сечения, показанного на рисунке а:
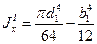 .
.
Дня этого сечения постоянным остается и момент сопротивления
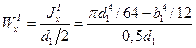 ,
,
так как расстояние от нейтральной оси до максимально удаленных от нее точек сечения не изменяется.
Для сечения, показанного на рисунке б:
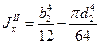
Для этого сечения при расположений, показанном на чертеже:
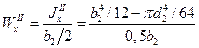 ,
,
а при повернутом на 450, когда нейтральная ось совпадает с одной из диагоналей квадрата,
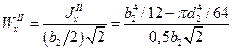 .
.
Таким образом, при повороте второго из заданных сечений на 450 допускаемая нагрузка соответствующей балки уменьшится на 29%.
Тема: «Понятия о касательных напряжениях в продольных сечениях брусьев при прямом изгибе»
В поперечных сечениях балок, как было установлено выше, при чистом изгибе возникают только нормальные, а при поперечном, изгибе - как нормальные, так и касательные напряжения.
Из закона парности касательных напряжений следует, что в продольных сечениях балки, параллельных нейтральному слою, также возникают касательные напряжения (рисунок 1). Для данной точки балки касательное напряжение 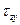 , возникающее на площадке поперечного сечения, равно касательному напряжению
, возникающее на площадке поперечного сечения, равно касательному напряжению 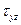 , возникающему на площадке продольного сечения, проведенного через ту же точку.
, возникающему на площадке продольного сечения, проведенного через ту же точку.
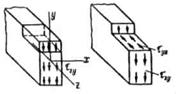
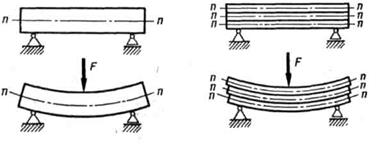
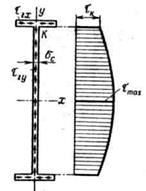
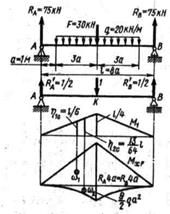
Рисунок 1. Рисунок 2. Рисунок 3.
Наличие касательных напряжений в продольных сечениях балок подтверждается также и результатами следующего простого опыта. Представим себе две одинаково нагруженные двухопорные балки (рисунок 2), одна из которых состоит из ряда отдельных положенных друг на друга и ничем не скрепленных брусьев. Каждый из этих брусьев деформируется независимо от других (влияние сил трения между брусьями не учитываем), имея собственный нейтральный слой. В результате деформации отдельные брусья, составляющие балку, взаимно сдвинутся. В целой балке взаимного сдвига ее продольных слоев не происходит; это и указывает на наличие в продольных плоскостях касательных напряжений, препятствующих этим сдвигам. Попутно заметим, что прогибы целой балки будут значительно меньше, чем балки, состоящей из отдельных брусьев.
Касательное напряжение в произвольной точке поперечного сечения бруса ( 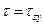 ) при прямом поперечном изгибе определяется по формуле
) при прямом поперечном изгибе определяется по формуле
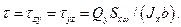
Здесь 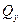 - поперечная сила, возникающая в рассматриваемом поперечном сечении бруса;
- поперечная сила, возникающая в рассматриваемом поперечном сечении бруса; 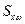 - статический момент относительно нейтральной оси поперечного сечения его части, расположенной по одну сторону от прямой, проведенной через исследуемую точку параллельно нейтральной оси;
- статический момент относительно нейтральной оси поперечного сечения его части, расположенной по одну сторону от прямой, проведенной через исследуемую точку параллельно нейтральной оси; 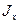 - момент инерции всего поперечного сечении относительно его нейтральной оси;
- момент инерции всего поперечного сечении относительно его нейтральной оси; 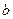 - ширина поперечного сечения — размер в направлении, параллельном нейтральной оси (при переменной ширине сечения значение
- ширина поперечного сечения — размер в направлении, параллельном нейтральной оси (при переменной ширине сечения значение 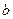 надо брать на уровне исследуемой точки).
надо брать на уровне исследуемой точки).
Эту зависимость называют формулой Журавского.
В балке прямоугольного сечения максимальные касательные напряжения возникают в тех точках, где нормальные напряжения равны нулю (на нейтральной оси), и, наоборот, в крайних точках сечения, где нормальные напряжения максимальны, касательные напряжения равны нулю. Сказанное справедливо также для балок круглого сечения.
Результат, полученный для балки прямоугольного сечения, можно использовать для вычисления касательных напряжений в стенке двутавровой балки. Не останавливаясь на доказательствах, укажем, что в полках двутавровых балок возникают горизонтально направленные касательные напряжения 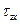 , а вертикальные
, а вертикальные 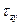 близки к нулю, при этом для вычисления последних формула Журавского неприменима. На рисунке 3 показано направление касательных напряжений в полке и стенках двутаврового профиля и дана эпюра
близки к нулю, при этом для вычисления последних формула Журавского неприменима. На рисунке 3 показано направление касательных напряжений в полке и стенках двутаврового профиля и дана эпюра 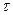 в стенке.
в стенке.
Напряжения в верхней (нижней) точке стенки найдем, подставляя в формулу 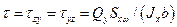 статический момент площади полки
статический момент площади полки 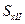 относительно нейтральной оси и принимая ширину сечения равной толщине стенки:
относительно нейтральной оси и принимая ширину сечения равной толщине стенки:
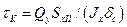 .
.
Максимальное касательное напряжение (возникает в точках нейтральной оси) найдем из выражения
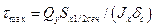 ,
,
где 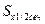 — статический момент полусечения относительно нейтральной оси.
— статический момент полусечения относительно нейтральной оси.
В прокатной или сварной двутавровой балке, имеющей сравнительно большую высоту, касательные напряжения могут быть значительны при условии, что балка нагружена большими сосредоточенными силами и длина ее невелика или эти силы приложены близко к опорам. В этом случае помимо основного расчета на прочность по нормальным напряжениям следует проверить максимальные касательные напряжения в том сечении, где поперечная сила имеет наибольшее значение. Обычно принимают (для стальных балок) 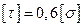 .
.
Тема: «Условия жесткости и расчета на жесткость при изгибе»
Работающие на изгиб элементы строительных и машиностроительных конструкций во многих случаях должны быть рассчитаны не только на прочность, но и на жесткость. При этом зачастую оказывается, что требуемые размеры поперечного сечения бруса (балки), определенные из расчета на жесткость, получаются большими, чем требуемые по условию прочности.
В большинстве случаев условие жесткости выражается неравенством
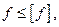
т. е. максимальный прогиб (стрела прогиба f) не должен превышать допускаемого 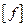 . Значение допускаемого прогиба зависит от назначения и условий работы рассчитываемой конструкции и колеблется в широких пределах. Обычно допускаемую стрелу прогиба указывают в долях пролета (межопорного расстояния
. Значение допускаемого прогиба зависит от назначения и условий работы рассчитываемой конструкции и колеблется в широких пределах. Обычно допускаемую стрелу прогиба указывают в долях пролета (межопорного расстояния 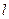 ) балки.
) балки.
Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости — ограничение угла поворота опорных сечений:
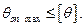
При этом допускаемый угол поворота составляет в среднем 0,001 рад.
В тех случаях, когда конструктивные и технологические требования не накладывают особых ограничений на форму поперечных сечений проектируемого элемента конструкции, следует применять такие сечения, которые обеспечивали бы возможно большую жесткость при наименьшем расходе материала. Жесткость балки прямо пропорциональна моменту инерции Jx ее поперечного сечения относительно нейтральной оси, а расход материала (масса балки) прямо пропорционален площади сечения А. Для оценки рациональности формы поперечного сечения балки, размеры которой определяются из расчета на жесткость, удобна безразмерная характеристика 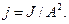
Для ускорения и упрощения расчетов на жесткость в таблице 1 приведены значения прогибов и углов поворота сечений для некоторых часто встречающихся балок.
Таблица 1
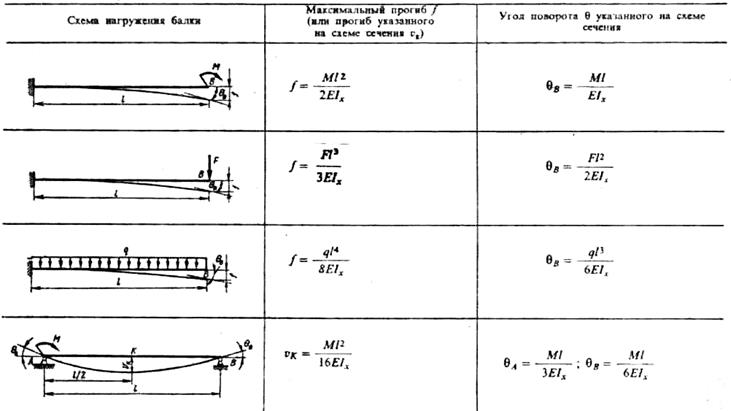
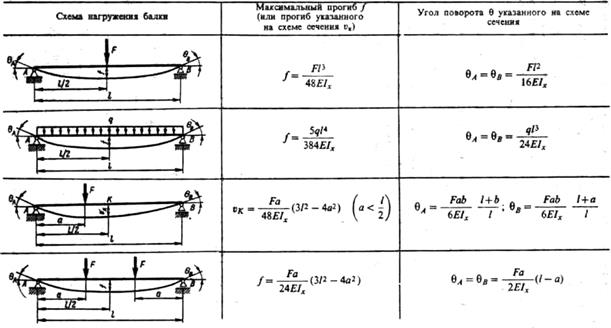
Задача.
Проверить прочность и жесткость стальной балки, если 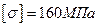 и
и 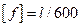 . Поперечное сечение балки - двутавр № 50;
. Поперечное сечение балки - двутавр № 50; 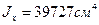 ;
; 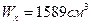 .
.
Решение.
Наибольший изгибающий момент возникает в сечении по середине пролета. В силу симметрии нагружения балки максимальным будет прогиб также по середине продета. Обращаем внимание на то, что сечении с максимальным изгибающим моментом и имеющее максимальный прогиб совпадают отнюдь не всегда.
Максимальный изгибающий момент 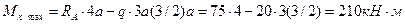 .
.
Максимальные нормальные напряжения в опасном сечении
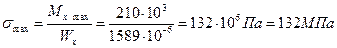 .
.
Максимальные напряженна ниже допускаемых на 17,5%.
Для определения максимального прогиба прикладываем к раздруженной балке по середине пролета единичную силу, строим эпюру 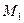 и расслоенную эпюру
и расслоенную эпюру 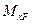 . Перемножая эпюры
. Перемножая эпюры 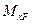 и
и 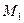 для одной половины балки и удваивая результат, найдем стрелу прогиба:
для одной половины балки и удваивая результат, найдем стрелу прогиба:
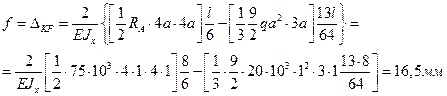
Допускаемый прогиб 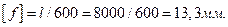
Следовательно, максимальный прогиб превышает допускаемый на 24,0 %, т.е. жесткость балки недостаточна.
Тема: «Совместное действие изгиба и растяжения (сжатия) на брусья большой жесткости»
 Рассмотрим сочетание пространственного изгиба и растяжения (или сжатия) прямого бруса (рисунок 1, а). Если в числе действующих на брус нагрузок есть силы, направления которых не совпадают ни с одной из главных центральных осей, их следует разложить на составляющие по этим осям, т. е. привести схему нагружения к аналогичной схеме, представленной на рисунке, 1, б.
Рассмотрим сочетание пространственного изгиба и растяжения (или сжатия) прямого бруса (рисунок 1, а). Если в числе действующих на брус нагрузок есть силы, направления которых не совпадают ни с одной из главных центральных осей, их следует разложить на составляющие по этим осям, т. е. привести схему нагружения к аналогичной схеме, представленной на рисунке, 1, б.
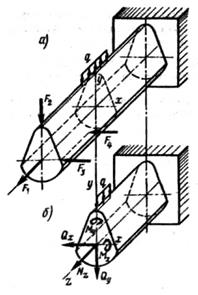
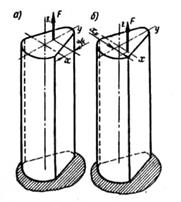
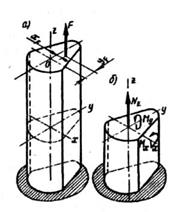
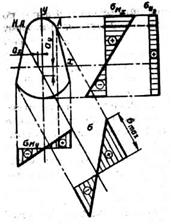
Рисунок 1. Рисунок 2. Рисунок 3. Рисунок 4.
В произвольном поперечном сечении бруса возникают пять внутренних силовых факторов (рисунок, 1, б): продольная сила 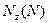 ; поперечные силы
; поперечные силы 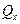 и
и 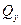 ; изгибающие моменты
; изгибающие моменты 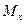 и
и 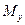 . В частных случаях некоторые из указанных величин могут быть равны нулю. Например, если равны нулю поперечная сила
. В частных случаях некоторые из указанных величин могут быть равны нулю. Например, если равны нулю поперечная сила 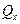 и изгибающий момент
и изгибающий момент 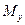 будет сочетание прямого изгиба в главной плоскости
будет сочетание прямого изгиба в главной плоскости 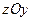 с растяжением или сжатием. Влияние поперечных сил учитывать не будем.
с растяжением или сжатием. Влияние поперечных сил учитывать не будем.
Для определения положения опасного поперечного сечения следует построить эпюры 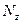 ,
, 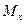 и
и 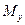 ; при этом может оказаться, что эти внутренние силовые факторы достигают своих наибольших значении не в одном и том же сечении. Следовательно, и расчет на прочность приходится выполнять для двух, а иногда и большего числа предположительно опасных сечений.
; при этом может оказаться, что эти внутренние силовые факторы достигают своих наибольших значении не в одном и том же сечении. Следовательно, и расчет на прочность приходится выполнять для двух, а иногда и большего числа предположительно опасных сечений.
Линейные перемещения определяют путем геометрического суммирования перемещений в трех взаимно перпендикулярных направлениях - вдоль осей х, у, z.
Применение принципа независимости сил при определении перемещений (а также внутренних силовых факторов и, следовательно, напряжении) допустимо лишь при условии, что, рассчитываемый брус обладает достаточно большой жесткостью. Для бруса малой жесткости было бы ошибочным определять прогибы только от нагрузки q, не учитывая влияния сжимающей силы F. Точно также, определяя изгибающий момент в каком-либо сечении, например в заделке, следует учесть, что в результате деформации бруса сила 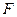 кроме сжатия вызывает и изгиб - дает в заделке изгибающий момент, равный
кроме сжатия вызывает и изгиб - дает в заделке изгибающий момент, равный 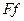 , который суммируется с моментом от нагрузки
, который суммируется с моментом от нагрузки 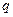 .
.
Будем считать, что рассчитываемый брус всегда имеет настолько большую жесткость что, можно не учитывать изменений, происходящих в расположении сил при его деформировании (так называемый принцип начальных размеров), и вести расчет на основе принципа независимости действия сил.
При нагружении бруса внеценренно приложенной силой, параллельной его продольной оси (рисунок 2, а), также получается сочетание изгиба с растяжением или сжатием (в зависимости от направления силы). Применив метод сечений, легко установить, что в любом поперечном сечении бруса возникают три внутренних силовых фактора (рисунок 2, б):
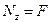 ;
; 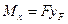 ;
; 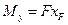
где 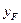 и
и 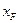 - координаты полюса (точки, приложения силы) в системе главных центральных осей.
- координаты полюса (точки, приложения силы) в системе главных центральных осей.
Таким образом, в общем случае внецентренного растяжения (сжатия) получается сочетание чистого косого изгиба с центральным растяжением или сжатием.
Чистый косой изгиб, в свою очередь, сводится к двум частым прямым изгибам во взаимно перпендикулярных плоскостях.
Конечно, определение каждого из изгибающих моментов как произведения силы на соответствующую координату полюса допустимо лишь при условии достаточно большой жесткости бруса, позволяющей пренебрегать изменениями расстояний от силы до главных осей какого-либо сечения, вызванными деформацией бруса.
В отличие от схемы нагружения на рисунке 1, а при внецентренном растяжении (сжатии) значения внутренних силовых факторов не зависят от положения поперечного сечения по длине бруса. Они одинаковы во всех поперечных сечениях (силу тяжести бруса не учитываем). Это обстоятельство упрощает расчет на прочность, так как вопрос об определении опасного сечения отпадает - здесь все сечения равноопасны.
В частных случаях, когда полюс находится не одной из главных центральных осей сечения (рисунок 3, а, б), получается сочетание чистого прямого изгиба с растяжением или сжатием. По схеме, данной на рисунке 3, а,- чистый изгиб относительно оси х и растяжение, а на рисунке 3, б - чистый изгиб относительно оси у и также растяжение.
Изгиб бруса будет прямым (независимо от положения полюса) также в случаях, когда форма поперечного сечения такова, что все его центральные оси - главные (круг, кольцо и т. п.).
Нормальные напряжения, возникающие в поперечном сечении бруса, нагруженного, как показано на рисунках 1 или 2, можно на основе принципа независимости действия сил рассматривать как результат наложения трех систем напряжений: определяемых его растяжением или сжатием ( 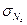 ), напряжений от прямого изгиба в главной плоскости
), напряжений от прямого изгиба в главной плоскости 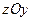 (
( 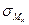 ), то же, прямого изгиба в главной плоскости
), то же, прямого изгиба в главной плоскости 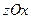 (
( 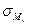 ).
).
Эпюры нормальных напряжений 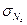 ,
, 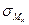 ,
, 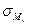 изображены на рисунке 4. Напряжения
изображены на рисунке 4. Напряжения 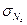 распределены по сечению равномерно, и соответствующая эпюра может быть расположена произвольно, но удобнее, когда ось этой, эпюры параллельна одной из главных центральных осей сечения, как показано на рисунке. Знаки на эпюрах поставлены в соответствии с направлениями внутренних силовых факторов, показанных на рисунках 1,б и 2, б.
распределены по сечению равномерно, и соответствующая эпюра может быть расположена произвольно, но удобнее, когда ось этой, эпюры параллельна одной из главных центральных осей сечения, как показано на рисунке. Знаки на эпюрах поставлены в соответствии с направлениями внутренних силовых факторов, показанных на рисунках 1,б и 2, б.
Нормальное напряжение в произвольной точке поперечного сечения определяется как алгебраическая сумма трех указанных напряжений: 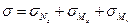 или
или 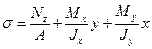
Каждое из слагаемых должно быть подставлено в эту формулу со своим знаком, определяемым по соответствующим эпюрам нормальных напряжений или, что то же самое, по характеру деформации бруса.
Для бруса из пластичного материала опасной будет точка, наиболее удаленная от нейтральной линии и условие прочности запишется в виде
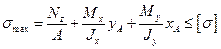
Для брусьев из хрупкого или хрупкопластичного материала в случаях 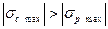 приходится вести расчет для двух точек. Условия, прочности:
приходится вести расчет для двух точек. Условия, прочности:
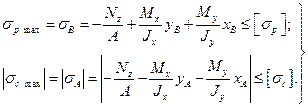
Для бруса из материала, различно сопротивляющегося растяжению и сжатию, условия прочности записываются в виде
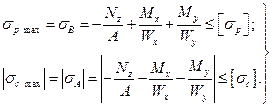
Тема: «Совместное действие изгиба с кручением и кручения с растяжением (сжатием)»
Валы различных машин представляют собой в большинстве случаев прямые брусья круглого сплошного или реже кольцевого сечения, работающие на совместное действие изгиба и кручения.
Применение гипотез прочности позволяет рассчитывать валы, учитывая совместное действие изгиба и кручения.
При расчете валов, а также других элементов конструкций, испытывающих одновременное действии изгиба и кручения, влиянием поперечных сил, как правило, пренебрегают, так как соответствующие им касательные напряжения в опасных точках бруса невелики по сравнению с касательными напряжениями от кручения и нормальными напряжениями от изгиба.
На рисунке 1, а показан вал, на который насажены зубчатое колесе диаметром 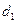 и шкив ременной передачи диаметром
и шкив ременной передачи диаметром 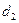 . На зубчатое колесо действуют окружная
. На зубчатое колесо действуют окружная 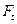 и радиальная
и радиальная 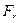 , силы, на шкив – силы
, силы, на шкив – силы 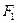 и
и 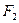 натяжения ветвей ремня. Для составления расчетной схемы вала (рисунок 1,б) все силы должны быть приведены к его оси. При переносе силы
натяжения ветвей ремня. Для составления расчетной схемы вала (рисунок 1,б) все силы должны быть приведены к его оси. При переносе силы 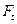 , к оси вала добавляется скручивающая пара с моментом
, к оси вала добавляется скручивающая пара с моментом 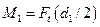 (рисунок 1, в); аналогично, при приведении сил
(рисунок 1, в); аналогично, при приведении сил 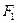 и
и 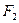 получается скручивающая пара с моментом
получается скручивающая пара с моментом 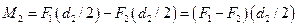 (Рисунок 1, г).
(Рисунок 1, г).
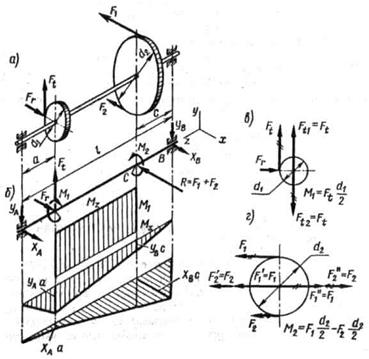
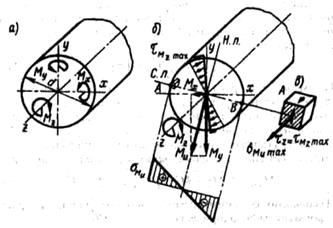
Рисунок 1. Рисунок 2
При равномерном вращении вала (только такой случай и рассматривается) 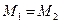 , что следует из основного уравнения динамики для вращательного движения.
, что следует из основного уравнения динамики для вращательного движения.
Подшипники, на которое опирается вал, рассматриваются при его расчете как пространственные шарнирные опоры, т. е. связи, препятствующие линейным перемещениям, но не мешающие повороту поперечных сечений вала.
На основе расчетной схемы определяют опорные реакции и строят эпюры 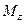 ,
, 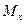 и
и 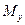 , по которым определяют опасное сечение вала. Как известно из предыдущего, расчет на изгиб бруса круглого поперечного сечения ведется по результирующему изгибающему моменту
, по которым определяют опасное сечение вала. Как известно из предыдущего, расчет на изгиб бруса круглого поперечного сечения ведется по результирующему изгибающему моменту 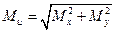 , следовательно, для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий
, следовательно, для вала, диаметр которого по всей длине постоянен, опасным будет сечение, в котором одновременно возникают наибольшие крутящий 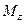 и изгибающий
и изгибающий 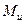 моменты. В рассматриваемом случае опасным будет сечение С под серединой шкива.
моменты. В рассматриваемом случае опасным будет сечение С под серединой шкива.
Проанализируем вопрос об опасных точках поперечного сечения. На рисунке 2, а показаны моменты в сечении, проведенном бесконечно близко слева от С. Применяя векторное изображение изгибающих моментов, найдем положение силовой и нулевой линий и построим зпюру нормальных напряжений 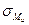 (рисунок 2, б). Касательные напряжения от кручения распределены вдоль любого радиуса по линейному закону и достигают максимального значения в точках контура сечения. Очевидно, опасными являются точки пересечения контура с силовой линией, в которых одновременно и нормальные напряжения от изгиба, и касательные напряжения от кручения имеют наибольшие значения.
(рисунок 2, б). Касательные напряжения от кручения распределены вдоль любого радиуса по линейному закону и достигают максимального значения в точках контура сечения. Очевидно, опасными являются точки пересечения контура с силовой линией, в которых одновременно и нормальные напряжения от изгиба, и касательные напряжения от кручения имеют наибольшие значения.
Для пластичного материала точки А и В равноопасны, для хрупкого или хрупкопластичного опаснее точка А, в которой от изгиба возникают нормальные напряжения растяжения.
На рисунке 2, в показан элемент, выделенный у опасной точки А, и возникающие на его гранях напряжения
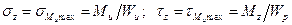 .
.
В опасной точке возникает упрощенное плоское напряженное состояние.
Валы, как правило, изготовляют из среднеуглеродистой конструкционной или реже легированной стали. Их расчет выполняют на основе третьей и пятой гипотез прочности.
Составим расчетную зависимость по третьей, гипотезе прочности.
По формуле 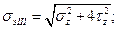 подставляя в нее значения
подставляя в нее значения 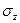 и
и 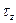 получаем
получаем
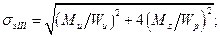 .
.
Учитывая, что для круглого (сплошного или кольцевого) сечения 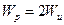 , имеем
, имеем
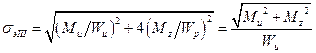
Внешне эта формула аналогична расчетной зависимости для определения максимальных нормальных напряжений при изгибе, поэтому величину, стоящую в числителе, называют эквивалентным (или приведенным) моментом, при этом условие прочности имеет вид
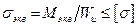 .
.
Таким образом, расчет бруса круглого поперечного сечения на изгиб с кручением ведется аналогично расчету на изгиб, но вместо изгибающего момента в расчетную формулу входит так называемый эквивалентный момент, который зависит от изгибающих и крутящего моментов, а также от принятой гипотезы прочности. По гипотезе наибольших касательных напряжений,
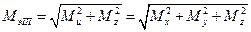 .
.
Независимо от применяемой гипотезы прочности расчетную формулу можно привести к виду 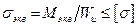 .
.
Если выполнить расчет по пятой теория прочности, то, воспользовавшись формулой 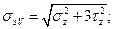 , после преобразовании, аналогичных рассмотренным, подучим
, после преобразовании, аналогичных рассмотренным, подучим
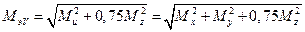 .
.
При проектном расчете определяют требуемое значение момента сопротивлении поперечного сечении:
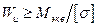 .
.
Учитывая, что для сплошного круглого сечения 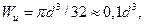 получаем следующую формулу для определения требуемого диаметра вала:
получаем следующую формулу для определения требуемого диаметра вала:
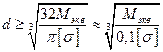 .
.
Понятие «эквивалентный момент» не имеет смысла при изгибе с кручением бруса некруглого поперечного сечения. Неприменимо оно и в случае, если помимо изгиба и кручения брус круглого сечения испытывает растяжение или сжатие.
Тема: «Гипотезы прочности и их назначение. Условие прочности при изгибе с кручением по различным гипотезам прочности»
В случае одноосного напряженного состояния оценка прочности в данной точке конструкции производится путем непосредственного сопоставления возникающего в ней рабочего напряжения либо с предельным, либо допустимым напряжением. Коэффициент запаса прочности равен отношению предельного напряжения к рабочему (расчетному): 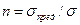 .
.
Предельное напряжение определяют при механических испытаниях данного материала на одноосное растяжение и сжатие. Для пластичных материалов за предельное напряжение принимают предел текучести 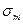 ; для хрупкопластичных материалов
; для хрупкопластичных материалов 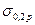 или
или 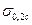 - условный предел текучести при растяжении или сжатии; дня хрупких материалов
- условный предел текучести при растяжении или сжатии; дня хрупких материалов 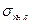 - предел прочности соответственно при растяжении или сжатии. В случае кручения (при чистом сдвиге) для многих материалов возможно также непосредственное определение коэффициента запаса прочности, так как имеются установленные экспериментально значения
- предел прочности соответственно при растяжении или сжатии. В случае кручения (при чистом сдвиге) для многих материалов возможно также непосредственное определение коэффициента запаса прочности, так как имеются установленные экспериментально значения 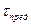 .
.
Возникает вопрос, как подойти к оценке прочности в общем случае сложного (объемного или плоского) напряженного состояния.
Пусть в исследуемой точке возникает напряженное состояние характеризуемое определенными из расчета главными напряжениями 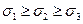 . Как известно из предыдущего, три главных напряжения полностью определяют напряженное состояние в данной точке тела. Допустим далее, что в лабораторных условиях для данного материала осуществлено напряженное состояние, подобное заданному в опасной точке рассчитываемой детали. Подобными называют напряженные состояния, для которых отношения главных напряжений одинаковы, т. е.
. Как известно из предыдущего, три главных напряжения полностью определяют напряженное состояние в данной точке тела. Допустим далее, что в лабораторных условиях для данного материала осуществлено напряженное состояние, подобное заданному в опасной точке рассчитываемой детали. Подобными называют напряженные состояния, для которых отношения главных напряжений одинаковы, т. е.
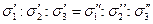 .
.
При некотором значений главных напряжений ( 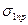 ,
, 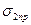 ,
, 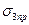 ) напряженное состояние в некоторой точке (точках) образца становится предельным, т. е. либо наступает текучесть, либо появляются признаки хрупкого разрушения. Величина, показывающая, во сколько раз нужно, увеличить возникающие в исследуемой точке, главные напряжения, для того чтобы напряженное состояние стало, предельным, представляет собой коэффициент запаса прочности
) напряженное состояние в некоторой точке (точках) образца становится предельным, т. е. либо наступает текучесть, либо появляются признаки хрупкого разрушения. Величина, показывающая, во сколько раз нужно, увеличить возникающие в исследуемой точке, главные напряжения, для того чтобы напряженное состояние стало, предельным, представляет собой коэффициент запаса прочности
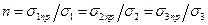 .
.
Подчеркиваем, что написанное выражение имеет смысл лишь в случае, если предельное состояние подобно заданному.
Практически изложенный подход к расчету на прочность при сложном напряженном состоянии возможен лишь в редких случаях. Действительно, разнообразие напряженных состояний безгранично, чрезвычайно велика также номенклатура применяемых материалов, и создать каждое из могущих встретиться на практике напряженных состояний, да к тому же для всех материалов в лабораторных условиях невозможно как по техническим, так и по экономическим причинам.
Следовательно, располагая ограниченными экспериментальными данными о свойствах определенного материала — значениями предельных напряжений при одноосном растяжении и сжатии, необходимо иметь возможность оценить его прочность в условиях любого сложного напряженного состояния. Это становится возможным при применении так называемых гипотез прочности (теорий предельных напряженных состояний)
Будем называть два напряженных состояния равноопасными или эквивалентными, если они переходят в предельные при, увеличении соответствующих им главных напряжений в одно и то же число ( 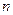 ) раз. Это означает, что коэффициенты запаса прочности для эквивалентных напряженных состояний одинаковы.
) раз. Это означает, что коэффициенты запаса прочности для эквивалентных напряженных состояний одинаковы.
Остается решить вопрос, что же является критерием (признаком) равноопасности различных по характеру (неподобных) напряженных состояний. Допустим, что решение этого вопроса существует (его дают гипотезы прочности). Тогда для расчета на прочность в случае сложного напряженного состояния следует заменить его равноопасным (эквивалентным) ему одноосным растяжением и сравнить соответствующее напряжение с предельным (или с допускаемым) для данного материала. Этот подход к оценке прочности при объемном (или плоском) напряженном состоянии иллюстрируется условной схемой, показанной на рисунке1.
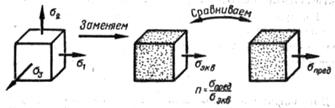
Рисунок 1.
Напряжение при одноосном растяжении заданному сложному напряженному состоянию называют эквивалентным напряжением 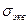 . Из приведенных рассуждений следует, что эквивалентное напряжение - это лишь некоторая условная расчетная величина, а не какое-либо реально возникающее напряжение. Значение эквивалентного напряжения зависит не только от заданного напряженного состояния (т. е: соответствующих ему главных напряжений), но и от принятого для расчета признака равноопасности напряженных состояний.
. Из приведенных рассуждений следует, что эквивалентное напряжение - это лишь некоторая условная расчетная величина, а не какое-либо реально возникающее напряжение. Значение эквивалентного напряжения зависит не только от заданного напряженного состояния (т. е: соответствующих ему главных напряжений), но и от принятого для расчета признака равноопасности напряженных состояний.
Гипотезы, указывающие признаки равноопасности (критерии эквивалентности) различных напряженных состояний, называют гипотезами прочности. Другие наименования: теория предельных напряженных состояний (гипотезы возникновения текучести и гипотезы прочности); гипотезы пластичности и хрупкого разрушения; теории прочности.
Как следует из изложенного, применение гипотез прочности избавляет от необходимости проведения громадного количества экспериментов. Эти эксперименты были бы неизбежны для установления предельных напряженных состояний, соответствующих различным комбинациям, возникающим в исследуемой точке детали главных напряжений. Вместе с тем сами гипотезы прочности нуждаются в экспериментальной проверке. Тот или иной критерий эквивалентности может быть основой для практических расчетов лишь при условии, что для ряда частных случаев он проверен опытным путем и результаты эксперимента оказались достаточно близки к результатам теоретического расчета.
Независимо от принятой гипотезы прочности после определения эквивалентного напряжения условие прочности можно представить в виде одного из следующих неравенств:
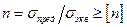
или
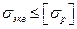 .
.
Рассмотрим критерии эквивалентности по трем гипотезам прочности, наиболее широко применяемым в современной расчетной практике, и приведем зависимости для вычисления эквивалентных напряжений.
Гипотеза наибольших касательных напряжений.
Согласно этой гипотезе, два напряженных состояния равноопасны, если максимальные касательные напряжения для них одинаковы.
Сформулированное условие, в частности, означает, что максимальные касательные напряжения для заданного напряженного состояния и эквивалентного ему одноосного растяжения одинаковы, т. е.
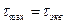 .
.
Для заданного напряженного состояния
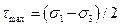 ;
;
для эквивалентного одноосного растяжения
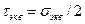
Учитывая, что рассматриваемую гипотезу часто называют третьей теорией прочности, будем обозначать эквивалентное напряжение 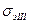 , с тем чтобы по этому обозначению без дополнительных пояснений было ясно, по какой гипотезе определяется эквивалентное напряжение. Так называемые первая я вторая теории прочности в настоящее время почти не применяются.
, с тем чтобы по этому обозначению без дополнительных пояснений было ясно, по какой гипотезе определяется эквивалентное напряжение. Так называемые первая я вторая теории прочности в настоящее время почти не применяются.
Приравнивая 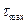 и
и 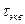 , получаем
, получаем
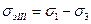 .
.
Очевидным недостатком этой гипотезы, обнаруживаемым даже по виду расчетной формулы, является пренебрежение влиянием промежуточного главного напряжения 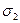 .
.
Гипотеза Мора.
Согласно этой гипотезе, два напряженных состояния равноопасны, если для соответствующих главных напряжений ( 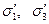 и
и 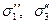 ) соблюдается соотношение
) соблюдается соотношение
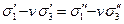 .
.
Отсюда, вытекает следующая формула для эквивалентного напряжения:
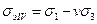
Индекс IV связан с тем, что эту гипотезу иногда называют четвертой теорией прочности. Коэффициент v представляет собой отношение предельных напряжений при одноосных растяжении и сжатии.
Гипотеза Мора не учитывает влияния промежуточного главного напряжения 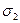 — это несомненный ее недостаток.
— это несомненный ее недостаток.
Гипотеза удельной потенциальной энергии изменения формы.
Согласно этой гипотезе, два напряженных состояния равноопасны, если удельная потенциальная энергия изменения формы для них одинакова.
Формулу для определения эквивалентного напряжения по рассматриваемой гипотезе, которую иногда называют пятой теорией прочности, имеет вид:
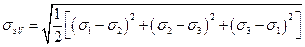 .
.
Эта гипотеза хорошо согласуется с опытными данными для пластичных материалов. Для них она точнее, чем гипотеза наибольших касательных напряжений. Подчеркнем, что согласно энергетической гипотезе условие эквивалентности определяется значениями всех трех главных напряжений.
Задача.
Сравнить опасность двух напряженных состояний (см. рисунок). Механические характеристики материалов имеют следующие значения: для первого элемента Дата добавления: 2019-09-30; просмотров: 1564;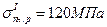 ,
, 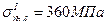 ; для второго элемента
; для второго элемента










