Тепловой пробой твердых диэлектриков

При сравнительно длительном воздействии напряжения на диэлектрик возможно значительное снижение его пробивного напряжения, связанное с выделением тепла в его толще. В этом случае пробой называется тепловым. Тепловой пробой может возникнуть, в частности, при длительном воздействии рабочего напряжения.

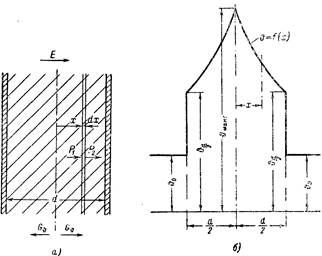
Рис. 4.3 – К расчету теплового пробоя диэлектрика в однородном поле. а— расчетная схема; б — распределение температуры по толще диэлектрика.

Под действием переменного напряжения через диэлектрик протекает емкостный ток (ток смещения) I_с и активный ток I_a, обусловленный диэлектрическими потерями в образце. Отношение I_a/I_c = tgδ называется коэффициентом диэлектрических потерь в изоляции. Для газовой изоляции при докоронных напряжениях tgδ практически равен нулю. Для твердых и жидких диэлектриков tgδ обычно лежит в пределах 0,01—0,03. С ростом температуры tgδ растет примерно по экспоненциальному закону

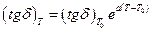(4.1)

где Т и T₀ – температуры, при которых определяется величина tgδ; а — постоянная. Выделяющееся в диэлектрике тепло расходуется на его нагрев. Основные закономерности наиболее просто удается рассчитать для плоского конденсатора с однородным диэлектриком (рис. 4.3,а), тепловой поток в котором направлен от центрального сечения диэлектрика к электродам, имеющим, как предполагается, постоянную температуру. Рассмотрим объем Sdx диэлектрика (S — площадь пластины конденсатора) на расстоянии х от оси конденсатора. В этом объеме выделяется мощность

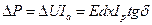(4.2)

Но

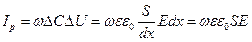(4.3)

Подставляя (4.3) в (4.2), получаем:

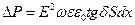(4.4)

Распространение тепла в твердом диэлектрике обусловлено напряженностью температурного поля 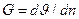, где п — координата в направлении наибольшего возрастания температуры. В конденсаторе на рис. 4.3,a 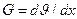. Тепловой поток (выраженный в ваттах), проходящий в единицу времени через поверхность S, равен P=kGS, где k — коэффициент внутренней тепловодности диэлектрика.

Тепловой поток, входящий в объем Sdx через сечение х, равен P₁ = kGS, а выходящий из этого объема через сечение x+dx равен 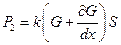. Их разность даст значение теплового потока, выходящего из объема Sdx:

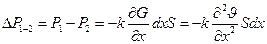(4.5)

Тепловое равновесие наступит, если этот поток будет равен мощности диэлектрических потерь в том же объеме ΔW. Из этого условия находим уравнение теплового баланса:

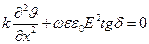(4.6)

Подставив в (4.6) зависимость (4.1), получаем:

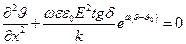(4.7)

На границе x=d/2 перепад температуры 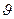равен:

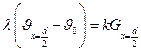(4.8)

где λ —коэффициент теплопроводности между диэлектриком и элек­тродом;

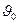— температура электродов, которая практически равна температуре окружающей среды (воздух, масло и т. п.). Решение уравнений (4.7) и (4.8) выражается функцией 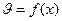, ход которой показан на рис. 4.3,б. Температура максимальна в среднем сечении. Чем выше напряженность Е при заданных tgδ₀ и а, тем выше температура 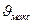. Эта зависимость показана на рис. 4.4.

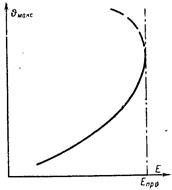
Рис. 4.4 – Зависимость максимальной температуры диэлектрика от напряженности поля.

При некоторой напряженности 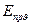касательная 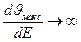Это и есть условие тепловой неустойчивости. При сколь угодно малом приращении Е температура 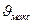будет расти неограниченно, что в конечном счете приведет к пробою изоляции. Пробивную напряженность 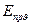можно определить из уравнения (4.7) по условию 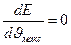для точек х=0, где температура максимальна.

Из изложенного следует, что тепловой пробой твердого диэлектрика есть проявление температурной неустойчивости на молекулярном уровне (в отличие от электрического пробоя).

Не останавливаясь на промежуточных, довольно сложных математических выкладках, приведем окончательные выражения для 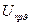твердого диэлектрика в плоском, а также цилиндрическом конденсаторах:

а) в плоском конденсаторе

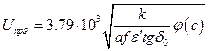(4.9)

б) в цилиндрическом конденсаторе

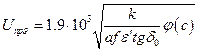(4.10)

В этих формулах: k — коэффициент внутренней теплопроводности диэлектрика, вт/см² °С;

а – температурный коэффициент tgδ, град^-1,

f – частота переменного тока, гц;

ε' – относительная диэлектрическая проницаемость;

tgδ₀ — начальное значение tgδ (при 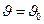); φ(c) – функция параметра c=αk/2k, показанная на рис. 4.5; α=d – вплоском конденсаторе и α = 2r₂ln(r₁/r₂) — в цилиндрическом конденсаторе; d и r — в сантиметрах; λ — коэффициент внешней теплопроводности между диэлектриком и электродом, вт/см²∙°С.

Изложенная теория теплового пробоя была разработана акад. В. А. Фоком.

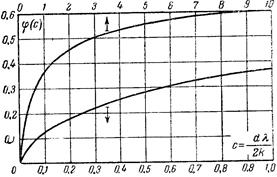
Рис. 4.5 – Зависимость φ(с) для расчета напряжения теплового пробоя.

Пример 4.1 Рассчитать пробивное напряжение стеклянной пластины толщиной d в пределах 1 – 4 см.

Коэффициент внутренней теплопроводности k для стекла равен 0,01 вт/см²∙°С, коэффициент внешней теплопроводности равен 0,017 вт/см²∙°С. Примем 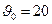°С (или 293°К). Значение tgδ₀=0,01, и температурный коэффициент a=0,0184 (°С^-1). Для стекла ε'=6.

Параметр c=αλ/2k при d, равном 1 и 4 см, будет соответственно равен: c(d=l см)=0,85; c(d = 4 см)= 3,4. По рис. 4.5 находим значения 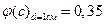, 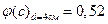. Подставив числовые значения в формулу (4.9), получим:

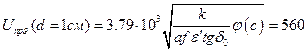кВ (4.11)

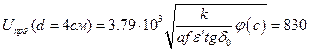кВ (4.12)

Произведя аналогичные расчеты для разных значений d, можно построить зависимость от d для величины среднего пробивного градиента .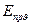

Пробивные градиенты падают с увеличением толщины образца, что объясняется ухудшением условий теплоотвода. Наоборот, малым толщинам должны соответствовать высокие 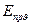. Однако в этом случае прочность диэлектрика определяется условиями электрического пробоя.

Пробивное напряжение снижается с повышением tgδ. Поэтому величина tgδ₀, которая обычно относится к температуре 20 °С, служит показателем прочности диэлектрика в отношении теплового пробоя. Резкое повышение tgδ₀ наблюдается при увлажнении диэлектрика. Поэтому увлажнение является наиболее вероятной причиной теплового пробоя. В наиболее тяжелых условиях находится изоляция (например трансформаторные вводы), нормально находящаяся при высокой температуре 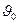и вследствие этого имеющая относительно высокий tgδ₀. К этой изоляции предъявляются повышенные требования в отношении значения при 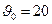°С.

Важной особенностью теплового пробоя служит зависимость 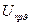от температуры окружающей среды 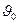. С ростом температуры 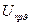снижается. Однако зависимость U_пр от температуры характерна также для электрического пробоя. Поэтому наличие такой зависимости еще не позволяет установить форму пробоя. Отличительной особенностью теплового пробоя является медленное его развитие, связанное с необходимостью разогрева диэлектрика под действием приложенного напряжения. Время пробоя снижается при возрастании U сверх 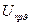,однако даже в худших случаях это время — порядка минут. При U,близких к 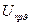, время пробоя исчисляется часами. Тепловой пробой наиболее вероятен в области наихудшего теплоотвода в изоляции. Электрический же пробой наиболее вероятен в области максимальных напряженностей поля на краях электродов.

Отметим еще, что сам термин «тепловой пробой» не вполнеточен. Пробой всегда имеет электрическую природу. Суть дела в том, что в результате тепловой нестабильности температура образца достигает значений, при которых возникает электропроводящий канал.

На постоянном напряжении потери в диэлектрике обусловлены только омической проводимостью материала, которая в здоровой изоляции очень мала. Поэтому на постоянном напряжении тепловой пробой указанного вида хотя принципиально и возможен, но в здоровой изоляции практически не возникает.