Лекция 2. Опытно-теоретический метод оценки показателей эффективности
Последовательность и содержание работ при использовании опытно-теоретического метода оценки показателей эффективности
Необходимость использования ОТМ оценки показателей эффективности БП и его сущность были рассмотрены выше (см.п. 1.1.1.)
Последовательность и содержание работ при использовании ОТМ оценки показателей эффективности кратко можно сформулировать следующим образом:
1. Содержательное описание задачи, связанной с оценкой эффективности, представляющее собой первый шаг на пути к ее формализации; уточнение степени и характера функциональной зависимости от характеристик составных частей, элементов БП, орудия и внешних условий; установление и выбор обобщенных параметров и показателей эффективности; определение требований по точности и достоверности получаемых оценок; отбор значимых факторов по априорным данным и т.д.;
2. Определение условий испытаний и выбор соответствующих методов оценки характеристик и показателей с учетом возможности использования информации о составных частях и изделия в целом, полученной различными способами (математическим моделированием, натурным экспериментом и т.д.);
3. Обоснование и выбор состава и структуры необходимых моделей и имитаторов.
4. Планирование и организация натурных испытаний, обоснование объема испытаний;
5. Отработка (калибровка) моделей по результатам натурных испытаний;
6. Оценка показателей эффективности в заданном диапазоне внешних условий.
Опытно-теоретический метод позволяет оценивать как отдельные характеристики и показатели составных частей, так и всего боеприпаса в целом в широком диапазоне условий эксплуатации (т.е. хранения транспортирования по назначению). При этом одновременно решается задача о наиболее рациональном использовании числа натурных испытаний и увязки их с результатами моделирования.
Основные принципы построения математических моделей
Моделирование – это экспериментирование на действующих физических и математических моделях, обладающих с некоторым приближением свойствами исследуемых реальных систем и их процессов.
Модели, используемые при испытаниях, можно классифицировать по основным признакам, следующим образом.
По способу отображения в модели реального процесса модели делятся на математические и физические. Математические модели по способу представления физических свойств процесса могут быть символическими и аналоговыми.
По виду моделируемого процесса все эти модели могут быть статическими и динамическими.
В зависимости от того, какой процесс реально рассматривается детерминистический или вероятностный модели могут быть детерминистическими или вероятностными.
По виду структурных связей вероятностные модели могут быть со стохастическими и детерминистическими связями.
При использовании ОТМ оценки эффективности боеприпасов находят применение вероятностные модели и более широкое – математические модели. Наглядно классификация моделей представлена на рисунке 1.2.
Классификация моделей.
| МОДЕЛИ |
| Физические |
| Математические |
| Статические |
| Динамические |
| Детерминистические |
| Вероятностные |
| Стохастические |
| С детерминистическими связями |
| Символические |
| Аналоговые |
По способу отображения в модели реального процесса
По способу представления физических свойств процесса
По виду моделируемого процесса
По виду структурных связей
Рисунок 1.2
Выбор структуры математических моделей, их отработка и оценка точности являются существенными для опытно-теоретического метода.
В общем случае для моделирования любого реального процесса можно построить множество различных моделей, отличающихся друг от друга той или иной степенью упрощения и приближения к оригиналу. В ОТМ целесообразно использовать максимально простые модели, учитывающие в своей структуре лишь те факторы и связи, значимость которых оказывается существенно заметной по выходным результатам. Но там как оценка значимости тех или иных факторов, а также и степени упрощения моделей, не может быть получена на основе общих рассуждений, то используют метод обработки моделей, позволяющий произвести оценку точности результатов моделирования. Суть методики отработки моделей сводится к выполнению следующей последовательности операций:
1. На основе априорных данных с учетом характера задач, для решения которых предназначается создаваемая модель, выбирают тип и структуру модели (полная, неполная, частичная) и отбирают релевантные факторы;
2. Для одних и тех же условий эксплуатации боеприпаса проводят несколько натурных экспериментов и набирают достаточное количество реализаций на модели. На основании сравнения результатов экспериментов и моделирования проводят параметрическую доработку модели при допущении, что выбранная ее структура удовлетворительна;
3. При наличии остаточной разности после параметрической доработки модели между выходными характеристиками по результатам сравнения данных эксперимента и моделирования на доработанной модели проводится структурная перестройка модели, заключающаяся в дополнительном учете отдельных факторов, значимость которых подтвердилась или к изменению и дополнению в структурной схеме модели отдельных связей;
4. Окончательно проверяют статистическую совместимость выходных характеристик по результатам натурных экспериментов и моделирования в ряде целенаправленно выбранных точек факторного пространства. Результаты в выбранных точках должны дать ответ не только о их статистической совместимости, но и характере поведения возможной методической ошибки моделирования во всей области рассматриваемого факторного пространства.
Подобный подход, как показала практика, позволяет создать работоспособную модель функционирования боеприпасов и достичь требуемой точности результатов моделирования.
Физическая модель – это упрощенные или уменьшенные «макеты» реальных систем.
Математическая модель представляет собой систему уравнений, описывающих функционирование боеприпаса и зависимость характеристик (показателей эффективности) всего боеприпаса от характеристик его составных частей, элементов и внешних условий.
В общем случае математическая модель может представлять собой систему дифференциальных, интегральных, алгебраических или смешанных уравнений.
Предположим, что математическая модель записана в виде
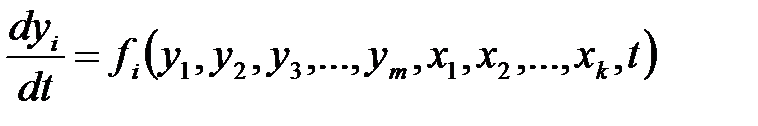 , (1.1)
, (1.1)
где 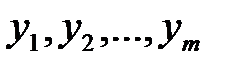 - оцениваемые характеристики (показатели);
- оцениваемые характеристики (показатели);
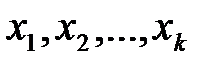 - параметры, характеризующие функционирование боеприпаса;
- параметры, характеризующие функционирование боеприпаса;
t - время.
Примером такой математической модели может служить система дифференциальных уравнений движения снаряда. Параметрами 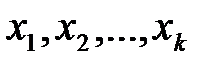 в этом случае будут начальные условия, параметры атмосферы, масса, моменты инерции, аэродинамические характеристики (Сх, Су, Сz…) и др. Поскольку реально они являются случайными величинами или случайными функциями, то и решения
в этом случае будут начальные условия, параметры атмосферы, масса, моменты инерции, аэродинамические характеристики (Сх, Су, Сz…) и др. Поскольку реально они являются случайными величинами или случайными функциями, то и решения 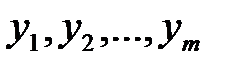 (например, координаты центра масс, составляющее скорости и ускорения, параметры движения вокруг центра масс и др.) являются случайными. Поэтому задача испытаний с помощью математической модели сводится к определению статистических характеристик решений системы (1.1). Чтобы определить статистические характеристики решений системы (1.1), необходимо знать статистические характеристики параметров
(например, координаты центра масс, составляющее скорости и ускорения, параметры движения вокруг центра масс и др.) являются случайными. Поэтому задача испытаний с помощью математической модели сводится к определению статистических характеристик решений системы (1.1). Чтобы определить статистические характеристики решений системы (1.1), необходимо знать статистические характеристики параметров 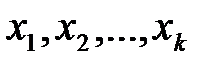 . Если выбрать их так, чтобы их легко было измерить при испытаниях, то используя эти измерения и математическое моделирование можно оценить интересующие нас характеристики или показатели эффективности системы (например, характеристики кучности стрельбы Вд, Вб).
. Если выбрать их так, чтобы их легко было измерить при испытаниях, то используя эти измерения и математическое моделирование можно оценить интересующие нас характеристики или показатели эффективности системы (например, характеристики кучности стрельбы Вд, Вб).
Рассматриваемая поставка задачи включает два направления: первое – создание математической модели, второе – накопление опытной информации на всех этапах опытной отработки и эксплуатации.
Приближенная методика калибровки математических моделей
При построении математических моделей выбором критерия оптимальности стремятся добиться такой эквивалентности модели реальной системе чтобы достичь некоторых вполне определенных свойств оценок, характеризующих показатели качества исследуемых изделий.
В самом общем случае критерий оптимальности определяет степень близости оценки показателя эффективности 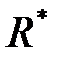 к его истинному значению
к его истинному значению 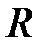 . Обычно качество оценки характеризуют с помощью некоторого заданного функционала
. Обычно качество оценки характеризуют с помощью некоторого заданного функционала 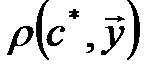 . Здесь c* – оценки параметров модели. Оценка
. Здесь c* – оценки параметров модели. Оценка 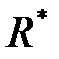 получена в результате статистического моделирования на математической модели, т.е. справедливо формальное равенство
получена в результате статистического моделирования на математической модели, т.е. справедливо формальное равенство 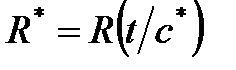 . Поэтому для каждого варианта построения модели функционал
. Поэтому для каждого варианта построения модели функционал 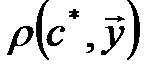 характеризует величину, зависящую от оценок вектора параметров модели c*. В свою очередь оценки вектора параметров модели функционально или статистически связаны с величинами или процессами
характеризует величину, зависящую от оценок вектора параметров модели c*. В свою очередь оценки вектора параметров модели функционально или статистически связаны с величинами или процессами 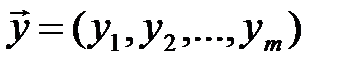 , которые наблюдались при проведении натурных экспериментов. Очевидно, что оценка вектор-параметров модели c* является случайной величиной. Поэтому целесообразно определить правило получения оценок
, которые наблюдались при проведении натурных экспериментов. Очевидно, что оценка вектор-параметров модели c* является случайной величиной. Поэтому целесообразно определить правило получения оценок 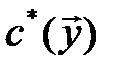 из условий минимизации функционала
из условий минимизации функционала
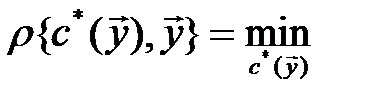 . (1.2)
. (1.2)
Однако, как показывает анализ [ ], решение задачи минимизации (1.2) связано со значительными трудностями. В связи с этим на практике обычно используют приближенную методику калибровки математических моделей по результатам натурных экспериментов.
Рассмотрим суть такой методики применительно к схеме, изображенной на рисунке 1.3.
На рисунке 1.3 приняты следующие обозначения:
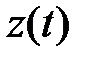 - реальный процесс на выходе реальной системы (или выходные характеристики в определенные моменты времени);
- реальный процесс на выходе реальной системы (или выходные характеристики в определенные моменты времени);
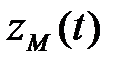 - то же на выходе модели;
- то же на выходе модели;
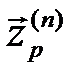 - оценка процесса на выходе реальной системы, полученная по результатам n натурных испытаний;
- оценка процесса на выходе реальной системы, полученная по результатам n натурных испытаний;
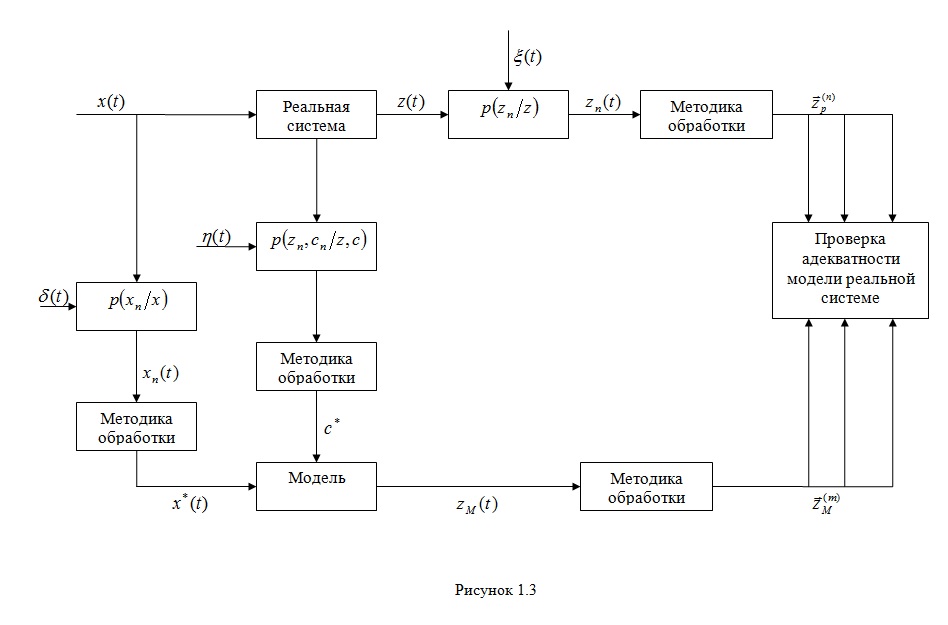
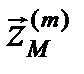 - то же по m реализациям модели;
- то же по m реализациям модели;
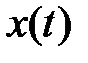 - внешние факторы, воздействующие на реальную систему;
- внешние факторы, воздействующие на реальную систему;
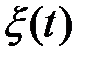 ,
, 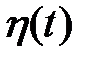 ,
, 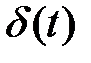 - соответствующие помехи с нулевыми математическими ожиданиями.
- соответствующие помехи с нулевыми математическими ожиданиями.
Если в математической модели пользоваться оценками параметров 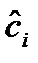 (i = 1,2,…,k), полученными на основании методов, разработанных для каждой отдельной составной части, то оценки показателя эффективности всего боеприпаса будут получаться неоптимальными и могут привести к неправильным выводам относительно выполнения боеприпасом заданных требований. В связи с этим возникает вопрос: а нельзя ли все же провести статистическое моделирование при найденных указанным выше образом оценках параметров модели
(i = 1,2,…,k), полученными на основании методов, разработанных для каждой отдельной составной части, то оценки показателя эффективности всего боеприпаса будут получаться неоптимальными и могут привести к неправильным выводам относительно выполнения боеприпасом заданных требований. В связи с этим возникает вопрос: а нельзя ли все же провести статистическое моделирование при найденных указанным выше образом оценках параметров модели 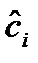 , а потом скорректировать оценки показателей эффективности боеприпаса так, чтобы они обладали всеми свойствами, которые предопределены выбранным критерием оптимальности.
, а потом скорректировать оценки показателей эффективности боеприпаса так, чтобы они обладали всеми свойствами, которые предопределены выбранным критерием оптимальности.
Возможности практической реализации такого подхода определяются сложностью выбранного критерия оптимальности и объемом моделирования, которое нужно провести для нахождения зависимости показателя эффективности R(t/c) как функции от вектора параметров c. Например, если выбором критерия оптимальности стремятся достичь определения точечных несмещенных оценок показателя R* , то можно скорректировать результаты моделирования, полученные на математической модели при введении в нее вектора оценок параметров c*, рассчитанного на основании методов, развитых для каждой составной части боеприпаса. В этом случае исследованию подлежат уравнения типа
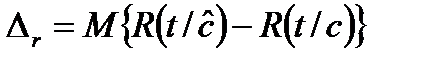 .(1.3.)
.(1.3.)
В уравнениях (1.3) операция математического ожидания осуществляется по распределению 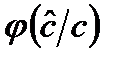 , определяющему множество всех возможных оценок
, определяющему множество всех возможных оценок 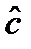 , которые могут быть получены в ходе физических экспериментов на элементах боеприпаса. Из-за высокой размерности вектора параметров c поиск точных решений уравнений (1.3) связан так же, как и при решений уравнений (1.2.), с довольно значительными трудностями вычислительного характера. Поэтому при разработке моделей конкретных БП задачу параметрической отработки моделей по результатам натурных испытаний, связанную с корректировкой результатов моделирования, рассматривают только относительно некоторых наиболее существенных факторов:
, которые могут быть получены в ходе физических экспериментов на элементах боеприпаса. Из-за высокой размерности вектора параметров c поиск точных решений уравнений (1.3) связан так же, как и при решений уравнений (1.2.), с довольно значительными трудностями вычислительного характера. Поэтому при разработке моделей конкретных БП задачу параметрической отработки моделей по результатам натурных испытаний, связанную с корректировкой результатов моделирования, рассматривают только относительно некоторых наиболее существенных факторов:
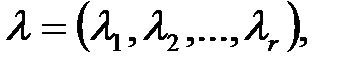
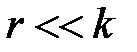 .
.
На практике математическая модель считается адекватной (в смысле возможностей практического использования результатов моделирования), реальной системе в том случае, когда доказано, что выборки моделируемых и реальных значений показателей эффективности системы имеют одинаковые законы распределения или принадлежат к одной и той же генеральной совокупности.
Для рассматриваемых условий методика калибровки моделей должна включать в себя следующие операции:
1. Обработка результатов натурных испытаний по единичным реализациям и по ансамблю реализаций на основе частных методик с целью получения исходных данных для моделирования (оценка параметров модели по результатам проведенных измерений).
Оценка параметров, для которых имеются априорные законы распределения, целесообразно осуществлять на основание байесовского подхода (т.е. определяются апостериорные законы распределения названных параметров), а при отсутствии априорной информации обработку результатов наблюдений производят с использованием методов максимального правдоподобия или наименьших квадратов.
2. Моделирование при исходных данных, полученных на основании частных методик обработки.
Основная цель такого моделирования – получить выборку значений выходного показателя 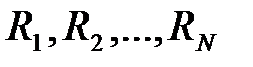 необходимого объема.
необходимого объема.
3. Корректировка результатов статистического моделирования из условий достижения их несмещенности. Необходимость этой операции объясняется хотя бы тем, что введение в модель оценок параметров 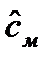 , полученных на основании метода максимального правдоподобия, приводит к тому, что оценки выходных показателей
, полученных на основании метода максимального правдоподобия, приводит к тому, что оценки выходных показателей 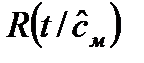 оказываются все же смещенными, даже если исходные параметры были несмещенными. Это является следствием того, что модель осуществляет нелинейное преобразование над входными воздействиями. Оценки выходного показателя
оказываются все же смещенными, даже если исходные параметры были несмещенными. Это является следствием того, что модель осуществляет нелинейное преобразование над входными воздействиями. Оценки выходного показателя 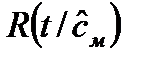 оказываются максимально правдоподобны, но вследствие указанной выше причины не удовлетворяют условно несмещенности оценок. Поэтому перед тем, как оценивать статистическую совместимость результатов моделирования с результатами натурных испытаний, нужно исключить смещение в результатах моделирования. Это позволит повысить точность получаемых результатов.
оказываются максимально правдоподобны, но вследствие указанной выше причины не удовлетворяют условно несмещенности оценок. Поэтому перед тем, как оценивать статистическую совместимость результатов моделирования с результатами натурных испытаний, нужно исключить смещение в результатах моделирования. Это позволит повысить точность получаемых результатов.
4. Проверка статистической совместимости результатов моделирования с результатами натурных испытаний.
При проверке этой гипотезы считаются заданными уровни значимости и тип используемого критерия. При выборе критерия обычно стремятся достичь такого положения, чтобы он для рассматриваемых условий позволял реализовать максимум вероятности правильного опознавания гипотезы в том случае, когда она верна, то есть использовать так называемый наиболее мощный критерий.
5. Принятие решения о пригодности модели к практическому использованию.
Такое решение обычно принимают по результатам проверки статистических гипотез о тождественности распределения моделируемых и реальных выборок. В случае, когда проверка гипотез дает положительный результат, модель считается в принятом смысле адекватной реальной системе и на ней можно проводить моделирование с целью определения показателей, характеризующих эффективность исследуемого боеприпаса.
Методы математического моделирования при испытаниях боеприпасов
Выше мы рассмотрели принципы разработки и калибровки математических моделей по результатам натурных испытаний. При этом мы еще не касались методов моделирования с использованием разработанной математической модели.
Обоснованный выбор метода математического моделирования в процессе опытной отработки такой сложной системы, какой является боеприпас, оказывает существенное влияние на повышение эффективности опытной отработки и качества создаваемого или модернизируемого образца.
В настоящее время получили распространение следующие методы математического моделирования:
- метод статистических испытаний (метод Монте-Карло);
- метод эквивалентных возмущений (метод Б.Г. Доступова);
- интерполяционный метод (метод В.И. Чернецкого).
Метод статистических испытаний
Для конкретности изложения будем полагать, что математическая модель записана в виде системы дифференциальных уравнений (1.1).
Сущность этого широко распространенного метода ясна из рисунка 1.4.
Общий алгоритм метода статистических испытаний
| нет |
| да |
| Ввод исходных данных |
Генерирование случайных чисел 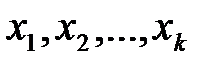 в соответст-вии с плотностями вероятности в соответст-вии с плотностями вероятности 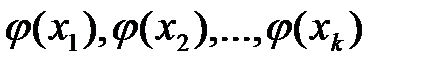 . .
|
Решение системы 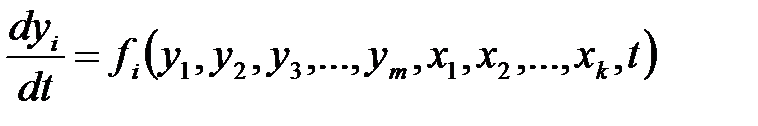 и нахождение
и нахождение 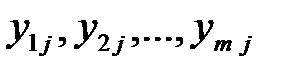 , j = 1,2,…,n , j = 1,2,…,n
|
Определение 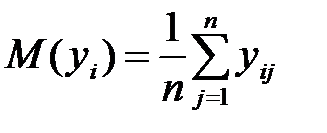 , ,
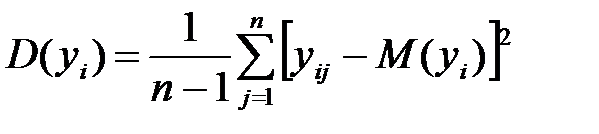
|
| Проверка условия n = nтр |
Рисунок 1.4
Метод реализуется, если случайные переменные 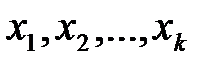 некоррелированы.
некоррелированы.
Его достоинствами являются простота реализации на вычислительных машинах, возможность получения законов распределения оцениваемых при моделировании характеристик, возможность получения все более и более точных оценок при увеличении числа статистических испытаний на модели (алгоритмы обработки обеспечивают при 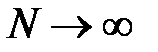
 сходимость по вероятности, т.е.
сходимость по вероятности, т.е. 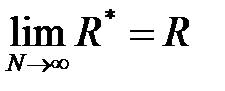 ).
).
К недостаткам метода статистических испытаний следует отнести тот факт, что этот метод для точностей, предъявляемых при практических оценках, приводит к довольно большому объему моделирования.
1.2.4.2. Метод эквивалентных возмущений
Метод применим в том случае, когда нас интересуют только математическое ожидание оцениваемой характеристики 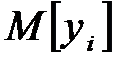 и дисперсия
и дисперсия 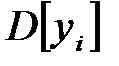 .
.
К достоинствам метода относятся следующие:
– при числе случайных переменных менее 20-30 объем вычислительных работ существенно меньше по сравнению с предыдущим;
– возможность проследить влияние каждого фактора 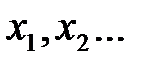 на случайные отклонения
на случайные отклонения 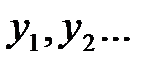 ;
;
– для задания 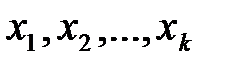 при моделировании нет необходимости обращаться к специальным программам выработки случайных чисел.
при моделировании нет необходимости обращаться к специальным программам выработки случайных чисел.
К недостаткам метода следует отнести:
– невозможность получить законы распределения оцениваемых при моделировании характеристик,
– сложность оценки точности получаемых при моделировании характеристик.
Сущность метода кратко заключается в следующем. Не снижая общности полученных ниже результатов будем полагать 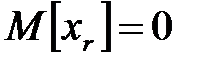 ,
, 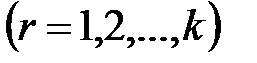 .
.
Будем полагать также, что существуют и известны моменты связи
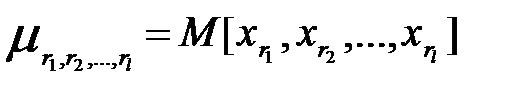 ,
, 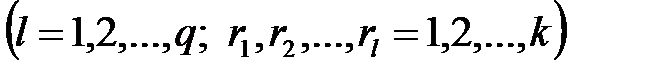 . (1.4)
. (1.4)
Решения системы (1.1) в общем случае можно представить в виде
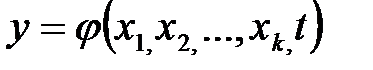 .
.
Предположим, что функция 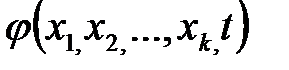 может быть разложена в ряд Маклорена по переменным
может быть разложена в ряд Маклорена по переменным 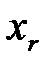 . Ограничиваясь членом q – й степени и опуская остаточный член, получим
. Ограничиваясь членом q – й степени и опуская остаточный член, получим
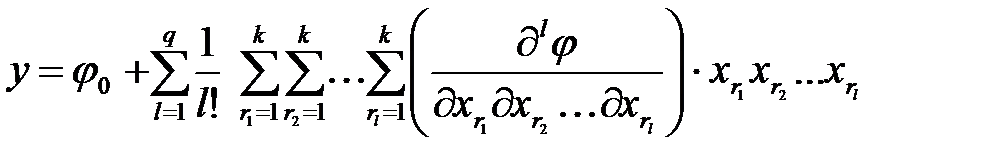 , (1.5)
, (1.5)
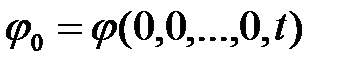 .
.
Подставим в выражение для 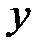 некоторые частные значения
некоторые частные значения 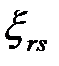 параметров
параметров 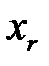 и проведем разложение функции
и проведем разложение функции 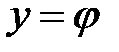 по этим параметрам. Аналогично (1.5) получим
по этим параметрам. Аналогично (1.5) получим
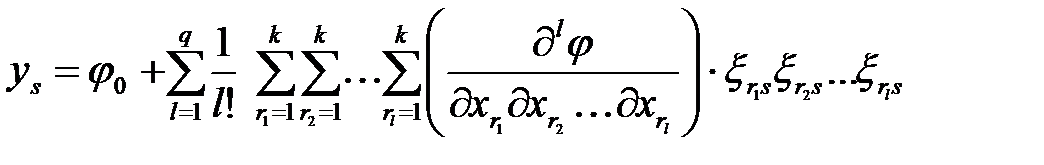 . (1.6)
. (1.6)
Величины 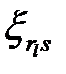 называются эквивалентными возмущениями. Выберем
называются эквивалентными возмущениями. Выберем 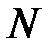 различных комбинаций эквивалентных возмущений
различных комбинаций эквивалентных возмущений 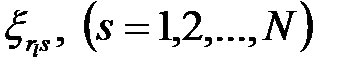
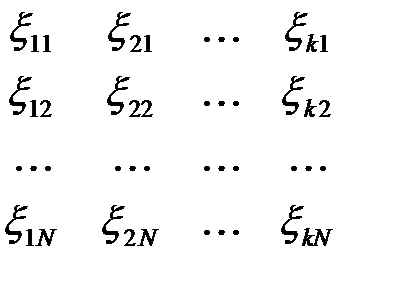
и подставим их в уравнение (1.6). Получим 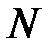 уравнений вида (1.5). Умножая обе части этих уравнений на некоторые, пока что неопределенные коэффициенты
уравнений вида (1.5). Умножая обе части этих уравнений на некоторые, пока что неопределенные коэффициенты 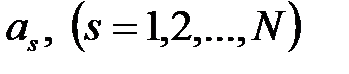 и суммируя полученные уравнения почленно, найдем
и суммируя полученные уравнения почленно, найдем
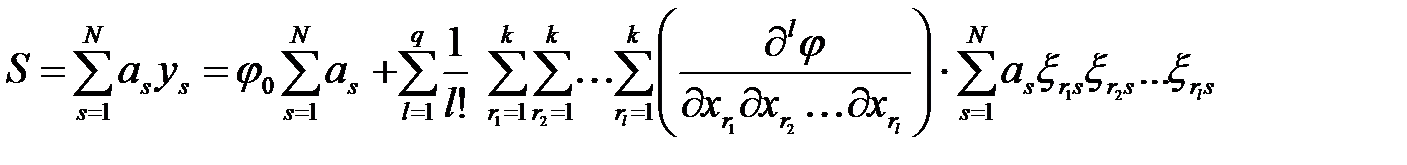 .(1.7)
.(1.7)
Математическое ожидание от (1.5) равно
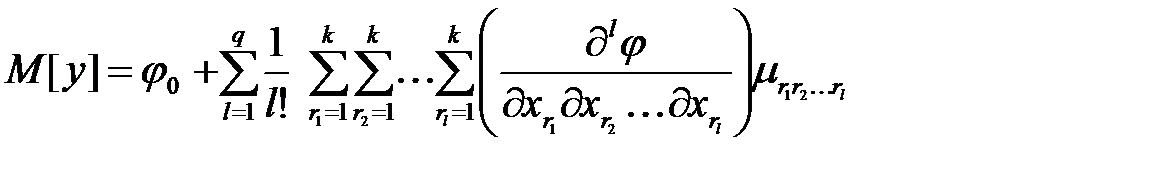 . (1.8)
. (1.8)
| (1.9) (1.10) |
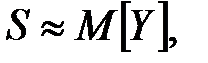
 если
если
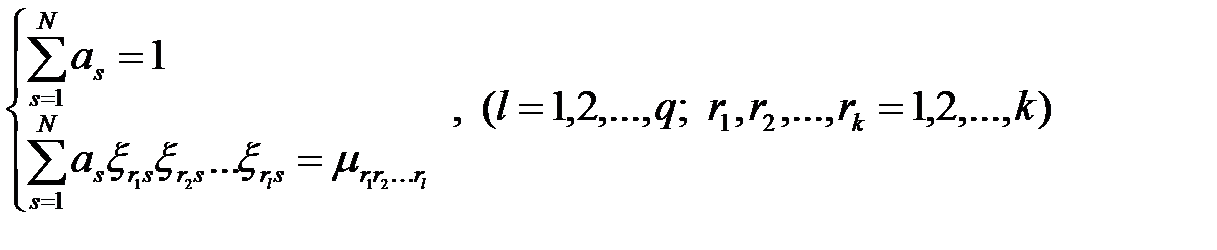 .
.
Выбирая в качестве величин 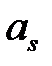 и
и 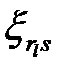 какое-либо действительное решение этой системы, получим
какое-либо действительное решение этой системы, получим
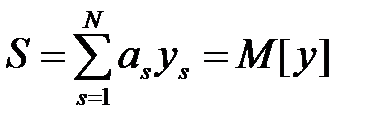 . (1.11)
. (1.11)
Величины 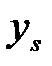 можно вычислить путем решения исходной системы (1.1.) при подстановке в эту систему соответствующих эквивалентных возмущений
можно вычислить путем решения исходной системы (1.1.) при подстановке в эту систему соответствующих эквивалентных возмущений 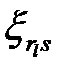 вместо случайных переменных
вместо случайных переменных 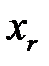 .
.
Аналогично можно показать, что
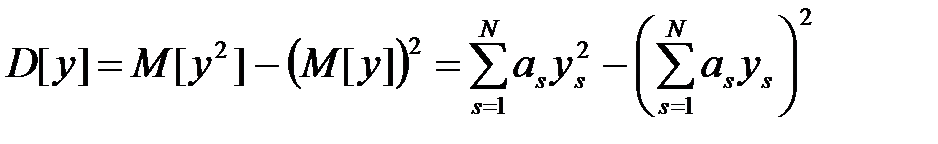 . (1.12)
. (1.12)
Точность полученных таким методом вероятностных характеристик зависит от вида уравнений (1.1) и степени аппроксимирующего полинома 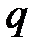 .
.
При q = 2 система уравнений (1.9), (1.10) запишется в виде:
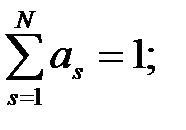 (1.13)
(1.13)
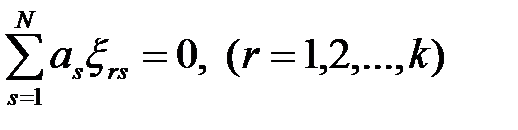 ; (1.14)
; (1.14)
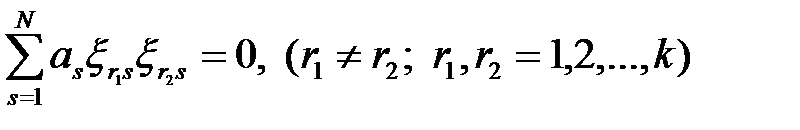 ; (1.15)
; (1.15)
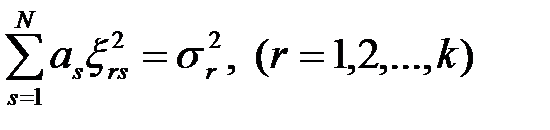 . (1.16)
. (1.16)
Число различных 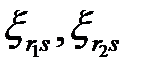 , при которых эта система уравнений имеет действительное решение, в общем случае определяется по формуле
, при которых эта система уравнений имеет действительное решение, в общем случае определяется по формуле
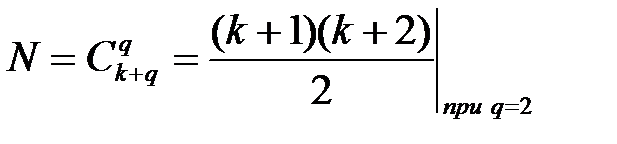
Специальным выбором 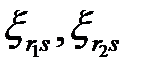 можно добиться обращения в ноль многих коэффициентов
можно добиться обращения в ноль многих коэффициентов 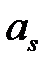 и существенно сократить число решений системы (1.1).
и существенно сократить число решений системы (1.1).
Предлагается, например, представить величины 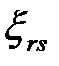 в соответствии с таблицей 1.1. [ 2 ]
в соответствии с таблицей 1.1. [ 2 ]
Таблица 1
| s | 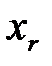
| ||||||
| . . . | k – 2 | k – 1 | k | ||||
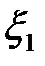
| . . . | ||||||
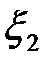
| . . . | ||||||
| . . . | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | ||||||
| k – 1 | . . . | 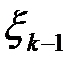
| |||||
| k | . . . | 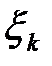
| |||||
| k + 1 | 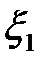
| 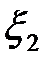
| 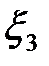
| . . . | 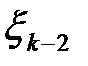
| 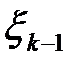
| 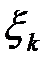
|
| k + 2 | - 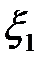
| - 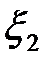
| - 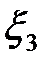
| . . . | - 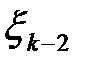
| - 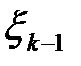
| - 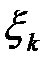
|
Примечание. Если 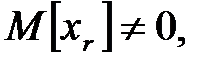 т.е.
т.е. 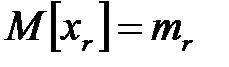 , то в таблице 1.1. вместо нулей необходимо записать
, то в таблице 1.1. вместо нулей необходимо записать 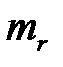 , а вместо
, а вместо 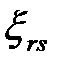 записать
записать 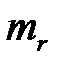 +
+ 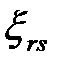 , вместо -
, вместо - 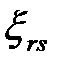 записать
записать 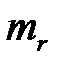 –
– 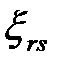 . В этом случае число решений системы (1.1)
. В этом случае число решений системы (1.1) 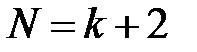 и первые два уравнения (1.13), (1.14) приводятся к виду
и первые два уравнения (1.13), (1.14) приводятся к виду
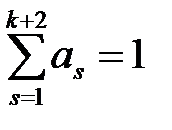 ; (1.17)
; (1.17)
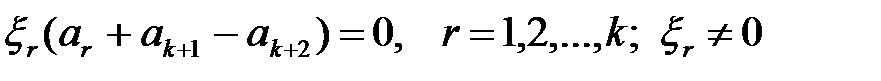 . (1.18)
. (1.18)
Суммируя все 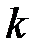 уравнений (1.18), найдем
уравнений (1.18), найдем
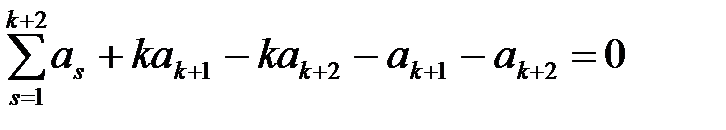 ,
,
или учитывая, что 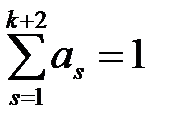 , получим
, получим
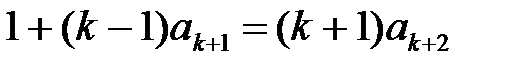 . (1.19)
. (1.19)
Уравнения (1.15), (1.16) в соответствии с таблицей 1.1 приводятся к виду:
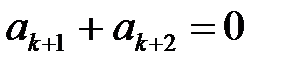 ; (1.20)
; (1.20)
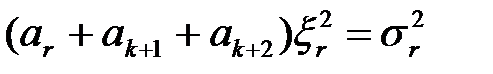 . (1.21)
. (1.21)
Отсюда имеем
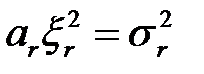 . (1.22)
. (1.22)
Из системы уравнений
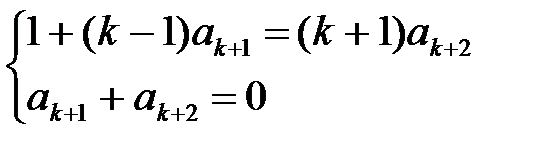
найдем
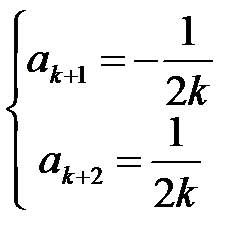 . (1.23)
. (1.23)
Подставив эти значения в уравнение (1.18), получим
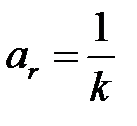 . (1.24)
. (1.24)
Подставив значение 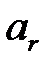 в (1.22), получим
в (1.22), получим
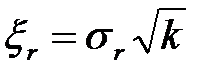 . (1.25)
. (1.25)
Таким образом, если в системе уравнений (1.1) содержится 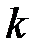 некоррелированных переменных
некоррелированных переменных 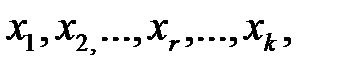 имеющих одинаковые законы распределения с известными математическими ожиданиями
имеющих одинаковые законы распределения с известными математическими ожиданиями 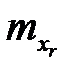 и среднеквадратическими отклонениями
и среднеквадратическими отклонениями 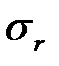 , то необходимо провести
, то необходимо провести 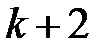 решения этой системы при подстановке в нее вместо случайных переменных эквивалентных возмущений, определенных по формуле (1.25), в соответствии с таблицей 1.1. В результате этих
решения этой системы при подстановке в нее вместо случайных переменных эквивалентных возмущений, определенных по формуле (1.25), в соответствии с таблицей 1.1. В результате этих 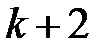 решений будет получено
решений будет получено 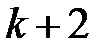 значения
значения 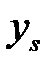
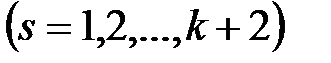 оцениваемых характеристик боеприпаса.
оцениваемых характеристик боеприпаса.
Имея эти значения 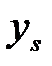 , учитывая значения известных теперь коэффициентов
, учитывая значения известных теперь коэффициентов 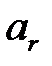 из формул (1.23), (1.24) и используя уравнения (1.11), (1.12), можно вычислить математическое ожидание и дисперсию по формулам:
из формул (1.23), (1.24) и используя уравнения (1.11), (1.12), можно вычислить математическое ожидание и дисперсию по формулам:
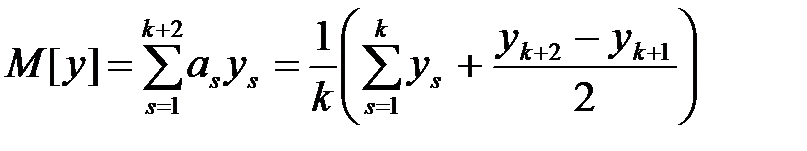 ; (1.26)
; (1.26)
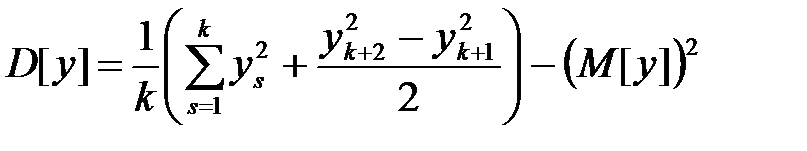 . (1.27)
. (1.27)
При кубической аппроксимации функции 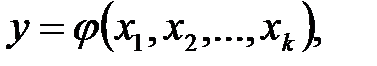 т.е. при
т.е. при 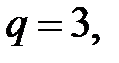 величины
величины 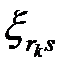 предлагается выбирать в соответствии с таблицей 1.2 [ 2 ].
предлагается выбирать в соответствии с таблицей 1.2 [ 2 ].
Таблица 1.2
| s | 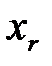
| |||||
| . . . | k - 1 | k | ||||
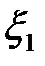
| . . . | |||||
- 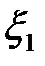
| . . . | |||||
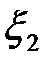
| . . . | |||||
- 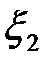
| . . . | |||||
| . . . | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | |||||
| 2k - 1 | . . . | 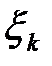
| ||||
| 2k | . . . | - 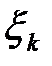
|
В рассматриваемом случае к системе уравнений (1.13) – (1.16) добавятся уравнения вида
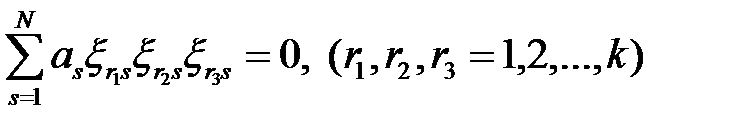 . (1.28)
. (1.28)
В соответствии с таблицей 1.2 будем иметь
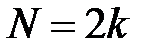 ; (1.29)
; (1.29)
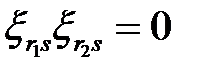 , при
, при 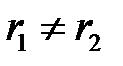 ; (1.30)
; (1.30)
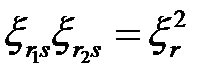 , при
, при 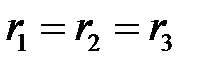 . (1.31)
. (1.31)
На основании равенства (1.30) заключаем, что все уравнения (1.15) при данном выборе величин 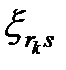 удовлетворяются. Уравнения (1.14), (1.16) и (1.28) приводятся к виду.
удовлетворяются. Уравнения (1.14), (1.16) и (1.28) приводятся к виду.
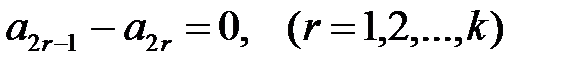 ; (1.32)
; (1.32)
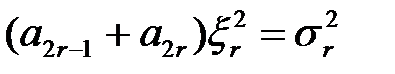 . (1.33)
. (1.33)
Выбирая все 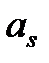 одинаковыми
одинаковыми 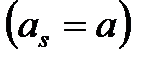 , удовлетворяем уравнениям (1.32), а из уравнений (1.13) и (1.33) получаем
, удовлетворяем уравнениям (1.32), а из уравнений (1.13) и (1.33) получаем
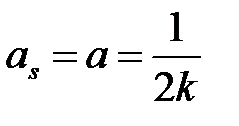 ; (1.34)
; (1.34)
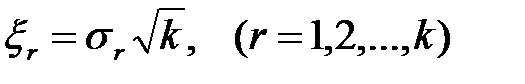 . (1.35)
. (1.35)
Если подставить в систему уравнений (1.1) вместо случайных переменных эквивалентные возмущения 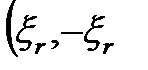 или
или 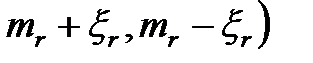 в соответствии с таблицей 1.2 и решить эту систему, то получим
в соответствии с таблицей 1.2 и решить эту систему, то получим 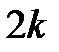 значений оцениваемой характеристики
значений оцениваемой характеристики 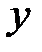 вида
вида
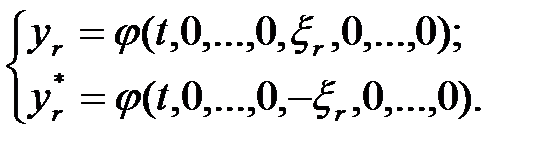 (1.36)
(1.36)
Математическое ожидание 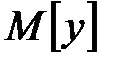 вычисляется по формуле
вычисляется по формуле
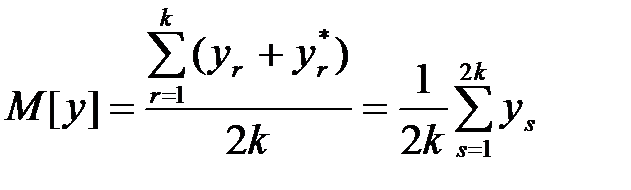 . (1.37)
. (1.37)
Дисперсия характеристики 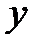 может быть определена по формуле
может быть определена по формуле
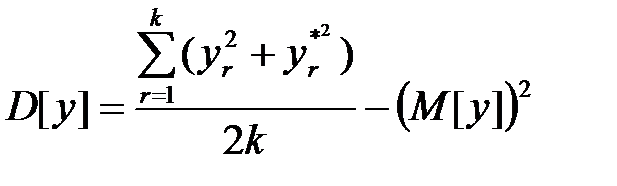 . (1.38)
. (1.38)
Если в системе уравнений (1.1) содержится только одна случайная переменная 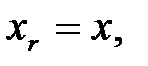 то формулы (1.37), (1.38) принимают вид
то формулы (1.37), (1.38) принимают вид
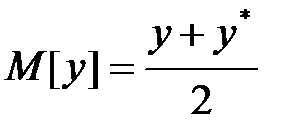 ;
;
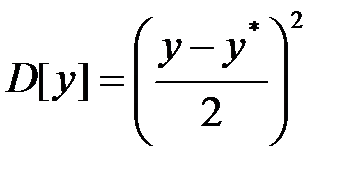 ,
,
т.е. математическое ожидание равно полусумме решений системы (1.1.), получающихся при подстановке вместо 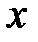 эквивалентных возмущений
эквивалентных возмущений 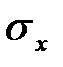 и –
и – 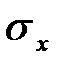 , а дисперсия равна квадрату полуразности этих решений.
, а дисперсия равна квадрату полуразности этих решений.
При большом числе случайных переменных (больших значений 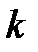 ) может оказаться, что величины
) может оказаться, что величины 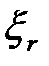 будут превосходить максимально возможные значения параметров
будут превосходить максимально возможные значения параметров 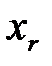 . При этом ошибка уравнения (1.5), обусловленная отбрасыванием остаточного члена разложения, может оказаться недопустимо большой.
. При этом ошибка уравнения (1.5), обусловленная отбрасыванием остаточного члена разложения, может оказаться недопустимо большой.
Однако можно легко получить формулы для определения математического ожидания и дисперсии характеристики 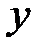 , не требующие подстановки больших значений
, не требующие подстановки больших значений 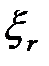 . Выберем
. Выберем 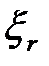 , фигурирующие в таблице 1.2, пропорциональными соответствующим среднеквадратическим отклонениям
, фигурирующие в таблице 1.2, пропорциональными соответствующим среднеквадратическим отклонениям 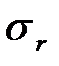 :
:
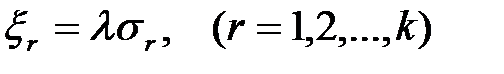 , (1.39)
, (1.39)
где 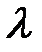 – постоянный коэффициент, не зависящий от
– постоянный коэффициент, не зависящий от 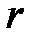 .
.
Можно получить для вычисления математического ожидания оцениваемой характеристики 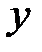 формулу [ 2 ]
формулу [ 2 ]
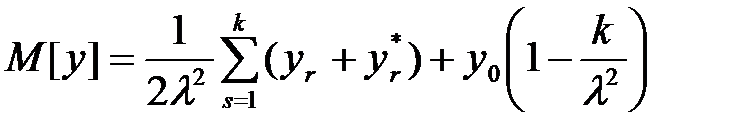 , (1.40)
, (1.40)
где 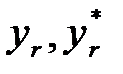 определяются уравнениями (1.36), а
определяются уравнениями (1.36), а 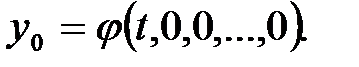 При
При 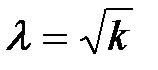 эта формула совпадает с (1.37).
эта формула совпадает с (1.37).
Интерполяционный метод
В отличие от метода эквивалентных возмущений интерполяционный метод разработан также и для расчета функций распределения вероятностей оцениваемых характеристик [ ], т.е. обладает такой же универсальностью, что и метод статистических испытаний (Метод Монте-Карло).
За счет оптимального выбора узлов интерполирования при одном и том же числе вариантов решений системы уравнений (1.1) интерполяционный метод дает более высокую точность, чем метод эквивалентных возмущений.
Имеются таблицы [ ] оптимальных чисел 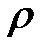 (числа Кристоффеля) и оптимальных вариантов узлов интерполирования (узлов Чебышева) для случайных величин, имеющих равномерный, нормальный или экспоненциальный законы распределения.
(числа Кристоффеля) и оптимальных вариантов узлов интерполирования (узлов Чебышева) для случайных величин, имеющих равномерный, нормальный или экспоненциальный законы распределения.
При практических расчетах необходимо преобразовать исходные случайные переменные к той или иной стандартной форме в зависимости от их законов распределения.
Если случайная величина 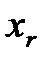 имеет равномерный закон распределения в промежутке
имеет равномерный закон распределения в промежутке 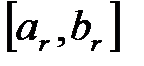 , то узлы типа Чебышева рассчитываются по формуле
, то узлы типа Чебышева рассчитываются по формуле
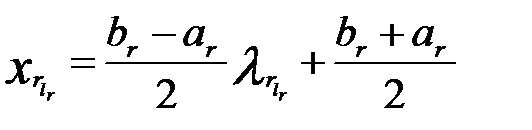 , (1.41)
, (1.41)
где 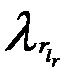 – стандартные узлы Чебышева для равномерного закона в промежутке [–1, 1].
– стандартные узлы Чебышева для равномерного закона в промежутке [–1, 1].
Если случайная величина 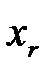 имеет нормальный закон распределения с параметрами
имеет нормальный закон распределения с параметрами 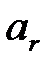 и
и 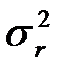 , то к стандартной форме она преобразуется по формуле
, то к стандартной форме она преобразуется по формуле
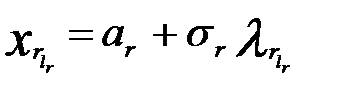 . (1.42)
. (1.42)
Стандартная случайная величина имеет распределение с параметрами 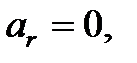
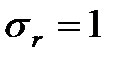 .
.
Случайная величина, имеющая экспоненциальное распределение с математическим ожиданием 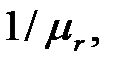 преобразуется к стандартной форме по формуле
преобразуется к стандартной форме по формуле
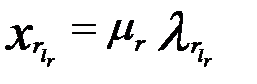 . (1.43)
. (1.43)
Математическое ожидание 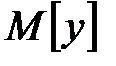 , дисперсия
, дисперсия 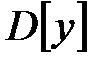
 и интегральный закон распределения
и интегральный закон распределения 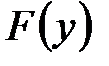 вычисляются по формулам:
вычисляются по формулам: 
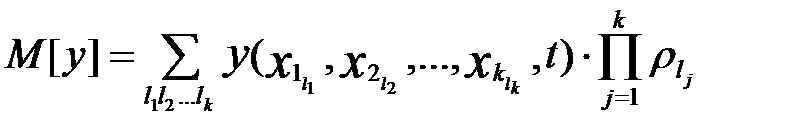 , (1.44)
, (1.44)
где 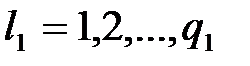 ;
; 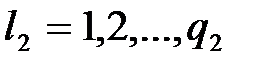 ; …
; … 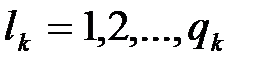 ;
;
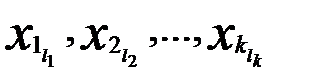
Дата добавления: 2022-05-27; просмотров: 113;










