Метод половинного деления
Пусть корень уравнения f(x)=0отделен на отрезке  [a;b], то есть на этом отрезке имеется единственный корень, а функция на данном отрезке непрерывна.
[a;b], то есть на этом отрезке имеется единственный корень, а функция на данном отрезке непрерывна.
Метод половинного деления позволяет получить последовательность вложенных друг в друга отрезков [a1;b1], [a2;b2], …,[ai;bi],…, [an;bn], таких что f(ai).f(bi) <0, где i=1,2,…,n, а длина каждого последующего отрезка вдвое меньше длины предыдущего:
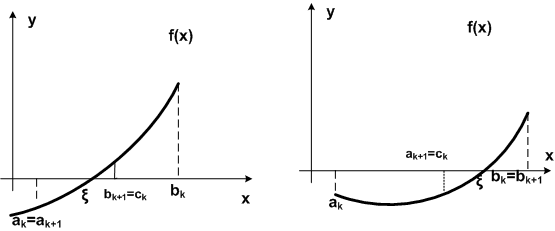
Рис.1.2.3-1
Последовательное сужение отрезка вокруг неизвестного значения корня  обеспечивает выполнение на некотором шаге n неравенства |bn - an|<e. Поскольку при этом для любого хÎ[an;bn] будет выполняться неравенство |
обеспечивает выполнение на некотором шаге n неравенства |bn - an|<e. Поскольку при этом для любого хÎ[an;bn] будет выполняться неравенство | 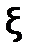 - х|<
- х|<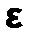 , то с точностью
, то с точностью 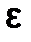 любое
любое
 может быть принято за приближенное значение корня, например его середину отрезка
может быть принято за приближенное значение корня, например его середину отрезка 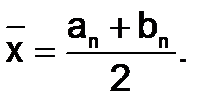
В методе половинного деления от итерации к итерации происходит последовательное уменьшение длины первоначального отрезка [a0;b0]в два раза (рис. 1.2.3-1). Поэтому на n-м шаге справедлива следующая оценка погрешности результата:
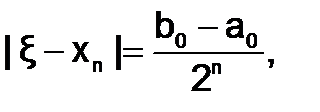 (1.2.3-1)
(1.2.3-1)
где  - точное значение корня, хnÎ [an;bn] – приближенное значение корня на n-м шаге.
- точное значение корня, хnÎ [an;bn] – приближенное значение корня на n-м шаге.
Сравнивая полученную оценку погрешности с заданной точностью  , можно оценить требуемое число шагов:
, можно оценить требуемое число шагов:
 (1.2.3-2)
(1.2.3-2)
Из формулы видно, что уменьшение величины e (повышение точности) приводит к значительному увеличению объема вычислений, поэтому на практике метод половинного деления применяют для сравнительно грубого нахождения корня, а его дальнейшее уточнение производят с помощью других, более эффективных методов.
| |
Рис. 1.2.3-2. Схема алгоритма метода половинного деления
Схема алгоритма метода половинного деления приведена на рис. 1.2.3-2. В приведенном алгоритме предполагается, что левая часть уравнения f(x)оформляется в виде программного модуля.
Пример 1.2.3-1.Уточнить корень уравнения x3+x-1=0 с точностью  =0.1, который локализован на отрезке [0;1].
=0.1, который локализован на отрезке [0;1].
Результаты удобно представить с помощью таблицы1.2.3-3.
Таблица 1.2.3-3
| k | a | b | f(a) | f(b) | (a+b)/2 | f((a+b)/2) | a k | b k |
| -1 | 0.5 | -0.375 | 0.5 | |||||
| 0.5 | -0.375 | 0.75 | 0.172 | 0.5 | 0.75 | |||
| 0.5 | 0.75 | -0.375 | 0.172 | 0.625 | -0.131 | 0.625 | 0.75 | |
| 0.625 | 0.75 | -0.131 | 0.172 | 0.688 | 0.0136 | 0.625 | 0.688 |
Послечетвертой итерации длина отрезка |b4-a4|=|0.688-0.625|=0.063 стала меньше величины e, следовательно, за приближенное значение корня можно принять значение середины данного отрезка: x = (a4+b4)/2 = 0.656.
Значение функции f(x) в точке x=0.656 равно f(0.656)= -0.062.
Метод итерации
Метод итераций предполагает замену уравнения f(x)=0 равносильным уравнением x=j(x). Если корень уравнения отделен на отрезке [a;b], то исходя из начального приближения x0Î[a;b], можно получить последовательность приближений к корню
x1 = j(x0), x2 = j(x1), …,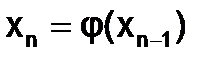 ,(1.2.3-3)
,(1.2.3-3)
где функция j(x) называется итерирующей функцией.
Условие сходимости метода простой итерации определяется следующей теоремой.
Пусть кореньх* уравнения x=j(x)отделен на отрезке [a;b]и построена последовательность приближений по правилу xn=j(xn-1). Тогда, если все члены последовательности xn=j(xn-1)Î [a;b]и существует такоеq (0<q<1), что для всех хÎ [a; b]выполняется |j’(x)| = q<1, то эта последовательность является сходящейся и пределом последовательности является значение корня x*, т.е. процесс итерации сходится к корню уравнения независимо от начального приближения.
Таким образом, если выполняется условие сходимости метода итераций, то последовательность x0, x1, x2, …, xn,…,полученная с помощью формулы xn+1 = j(xn), сходится к точному значению корня 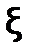 :
:
если 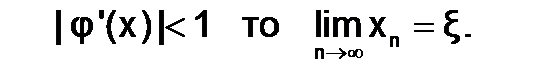
Условие j(x)Î[a;b] при xÎ[a;b] означает, что все приближения x1, x2, …, xn,…,полученные по итерационной формуле, должны принадлежать отрезку [a;b], на котором отделен корень.
Для оценки погрешности метода итерации справедливо условие
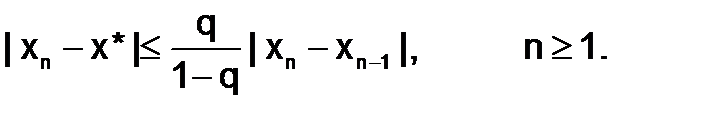 (1.2.3-4)
(1.2.3-4)
За число q можно принимать наибольшее значение |j'(x)|,а процесс итераций следует продолжать до тех пор, пока не выполнится неравенство
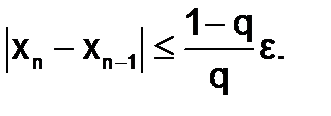 (1.2.3-5)
(1.2.3-5)
На практике часто используется упрощенная формула оценки погрешности. Например, если 0<q£½то
|xn-1 - xn|£ 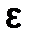 .
.
Использование итерационной формулы xn+1=j(xn) позволяет получить значение корня уравнения f(x)=0 с любой степенью точности.
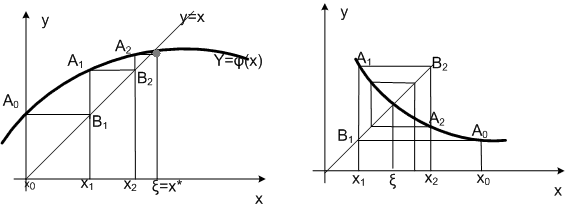
Геометрическая иллюстрация метода итераций. Построим на плоскости X0Y графики функций y=x и y=j(x). Корень уравнения х=j(x) является абсциссой точки пересечения графиков функции y = j(x) и прямой y=x. Возьмем некоторое начальное приближение x0Î [a;b]. На кривойy = j(x) ему соответствует точка А0 = j(x0). Чтобы найти очередное приближение, проведем через точку А0прямую горизонтальную линию до пересечения с прямой y = x (точкаВ1) и опустим перпендикуляр до пересечения с кривой (точкаА1), то естьх1=j(x0). Продолжив построение аналогичным образом, имеем ломаную линию А0, В1, А1, В2, А2…, для которой общие абсциссы точек представляют собой последовательное приближение х1, х2, …, хn («лестницу») к корню х*. Из рис. 1.2.3-3а видно, что процесс сходится к корню уравнения.
Рассмотрим теперь другой вид кривой y = j(x) (рис. 1.2.6b). В данном случае ломаная линия А0, В1, А1, В2, А2…имеет вид “спирали”. Однако, и в этом случае наблюдается сходимость.
a) b)
Рис. 1.2.3-3
Нетрудно видеть, что в первом случае для производной выполняется условие 0<j’(x)< 1,а во втором случае производная j’(x)<0иj’(x)>-1. Таким образом, очевидно, что если |j’(x)|<1, то процесс итераций сходится к корню.
Теперь рассмотрим случаи, когда |j’(x)|>1. На рис. 1.2.3-4а показан случай, когда j’(x)>1, а на рис. 1.2.3-4b – когда j’(x) < -1.В обоих случаях процесс итерации расходится, то есть, полученное на очередной итерации значение х все дальше удаляется от истинного значения корня.

a) b)
Рис. 1.2.3-4
Способы улучшения сходимости процесса итераций. Рассмотрим два варианта представления функции j(x) при переходе от уравнения f(x)кx=j(x).
1.Пусть функция j(x) дифференцируема и монотонна в окрестностях корня и существует числоk£ |j‘(x)|, где k³ 1 (т.е. процесс расходится). Заменим уравнение х=j(x) эквивалентным ему уравнением х=Y(х),где Y(х) = 1/j(x)(перейдем к обратной функции). Тогда

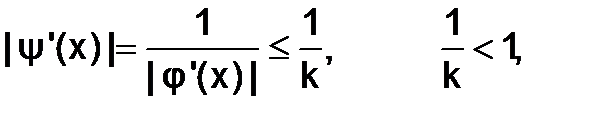 а значит q=1/k<1 и процесс будет сходиться.
а значит q=1/k<1 и процесс будет сходиться.
2.Представим функцию j(x) как j(x) = х - lf(x), где l- коэффициент,не равный
нулю. Для тогочтобы процесс сходился, необходимо, чтобы
0<|j¢(x)|=|1 - lf¢(x)|<1. Возьмем l= 2/(m1+M1), где m1иM1– минимальное и максимальное значенияf’(x) (m1=min|f’(x)|, M1=max|f’(x)|)для хÎ[a;b],т.е.0£ m1£ f¢(x) £ M1£1.Тогда
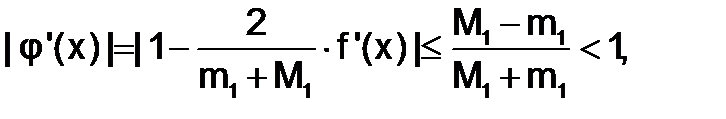
и процесс будет сходящимся, рекуррентная формула имеет вид
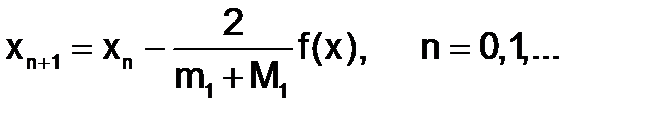
Если f¢(x) < 0, то в рекуррентной формуле f(x) следует умножить на -1.
Параметр λ может быть также определен по правилу:
Если 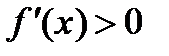 , то
, то 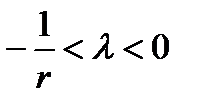 , а если
, а если  , то
, то 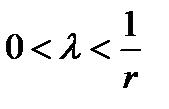 , где
, где 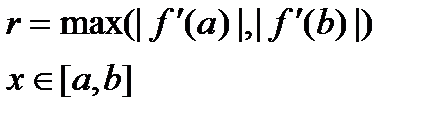 .
.
Схема алгоритма метода итерации приведена на рис. 1.2.3-5.
Исходное уравнение f(x)=0преобразовано к виду, удобному для итераций: 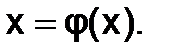 Левая часть исходного уравнения f(x) и итерирующая функция fi(x) в алгоритме оформлены в виде отдельных программных модулей.
Левая часть исходного уравнения f(x) и итерирующая функция fi(x) в алгоритме оформлены в виде отдельных программных модулей.
| |
Рис. 1.2.3-5. Схема алгоритма метода итерации
Пример 1.2.3-2.Уточнить корень уравнения 5x – 8∙ln(x) – 8 =0 с точностью 0.1, который локализован на отрезке [3;4].
Приведем уравнение к виду, удобному для итераций:
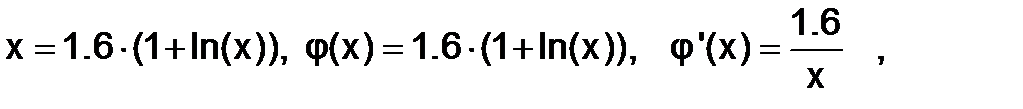


Следовательно, за приближенное значение корня уравнения принимаем значение x3=3.6892, обеспечивающее требуемую точность вычислений. В этой точке f(x3)=0.0027.
Дата добавления: 2016-05-31; просмотров: 3906;










