Метод конечных разностей.

Общий вид краевой задачи на отрезке для ОДУ второго порядка.

Краевая задача на отрезке 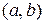для дифференциального уравнения второго порядка в общем случае представима в виде

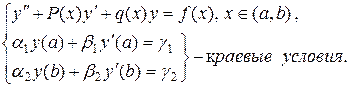(1.1)

Здесь все величины, кроме 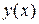, предполагаются заданными.

Отметим, что существует некоторое бесконечное множество функций, удовлетворяющих приведенному дифференциальному уравнению, и лишь наличие области изменения 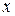( 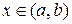– геометрическая характеристика конструкции) и условий на краях области обеспечивает единственность его решения. Однако и это решение (хотя оно и единственное), в общем случае, нельзя представить в аналитической форме. Поэтому, как правило, задача решается численным методом.

Метод конечных разностей.

Метод конечных разностей (МКР) – это наиболее простой и при этом достаточно эффективный способ численного решения краевой задачи. Его суть кратко опишем ниже.

Разобьем отрезок 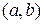на 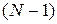отрезков (рис. 1.1).

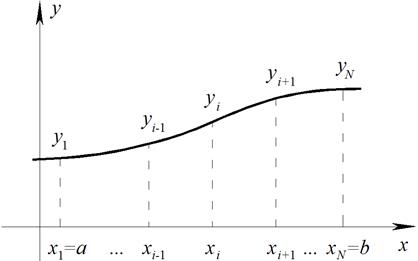
Рис. 1.1. Схема аппроксимации по методу конечных разностей.

Введем обозначения: 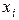– координаты точек разбиения (узлов); 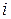– номер точки разбиения ( );

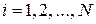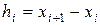(1.2)

– длина 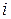-го отрезка (шаг разбиения);

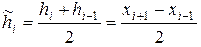(1.3)

– «средний» шаг;

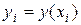, при этом 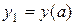, 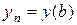; (1.4)

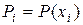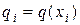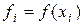; ; . (1.5)

Производные в 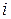-ой точке заменим разностными соотношениями:

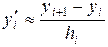(1.6)

– правая разность;

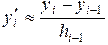(1.7)

– левая разность;

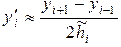(1.8)

– центральная разность.

При 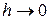в соответствии с известным определением производной все три величины будут стремиться к 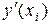. Использование той или другой из них зависит от конкретной ситуации.

Вторая производная в 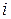-ой точке может быть приближенно представлена разностным отношением в виде разности от первых (вторая производная – это первая производная от первой производной), например

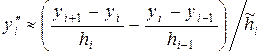. (1.9)

При 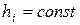формулу второй разности можно упростить:

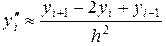. (1.10)

Пользуясь приведенными обозначениями и формулами, можно представить задачу (1.1) в каждой 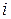-ой точке относительно величин 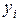следующим образом:

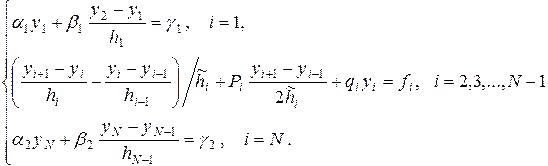(1.11)

Это и есть разностный аналог краевой задачи (1.1). Здесь 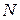неизвестных 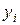и 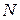линейных уравнений. Приводя подобные члены, получим систему линейных алгебраических уравнений относительно неизвестных величин :

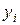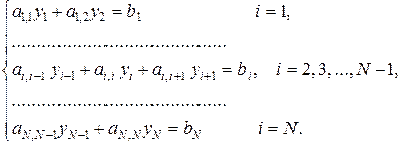(1.12)

или в матричном виде

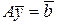, (1.13)

где

; ; ,

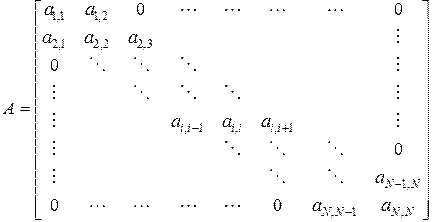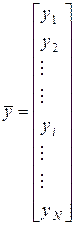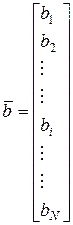(1.14)

при этом элементы матрицы и вектора правой части определяются формулами

, ; , ,

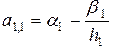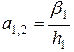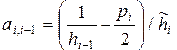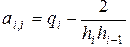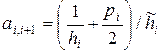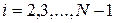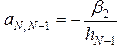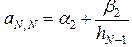, ; , ; (1.15)

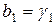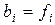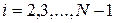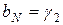; , ; . (1.16)

Следует отметить, что матрица 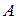трехдиагональная.

После решения системы (1.13) получим приближенное решение задачи (1.1) – значения искомой функции 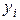в 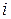-х точках. Соединяя 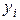ломаной линией, получаем приближенное решение 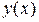во всех точках области .

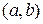Точность решения задачи (1.1) зависит от точности аппроксимации значений производных разностями, которая, в свою очередь, зависит от величины шага разбиения.