Порядок аппроксимации производных.

Для упрощения оценок предположим, что 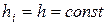. По формуле Тейлора получим:

,

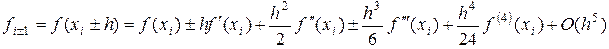где 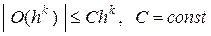. (1.17)

Тогда для правой разности получим

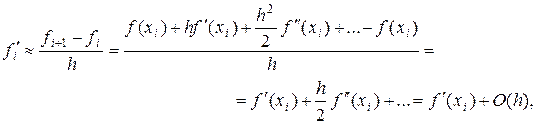
т.е. окончательно

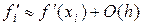(1.18)

и имеем аппроксимацию первого порядка.

Аналогично для левой разности

,

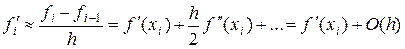т.е. также получаем результат (1.18) и первый порядок аппроксимации.

Рассмотрим также центральную разность.

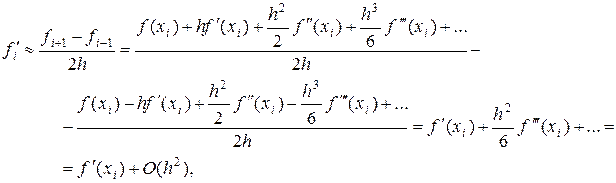
т.е. 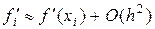(1.19)

и здесь имеем аппроксимацию второго порядка.

Следовательно, центральная разность является, как правило, более точной аппроксимацией первой производной.

Установим порядок аппроксимации для второй производной. Имеем:

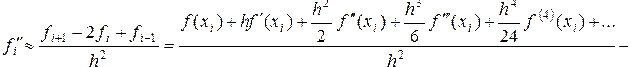
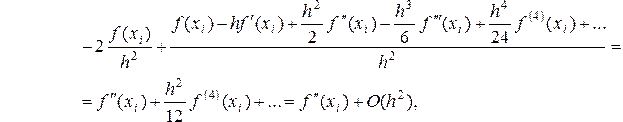
т.е. 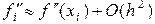. (1.20)

Итак, имеем аппроксимацию второго порядка. Аналогично можно установить порядок аппроксимации для любой разностной формулы.

1.4. Разностный аналог краевой задачи для случая .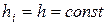

В этом случае вид системы (1.11) упрощается, а именно

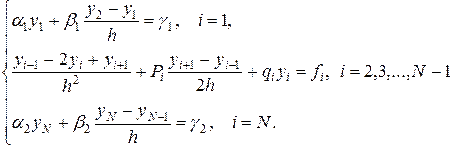(1.21)

Приводя подобные члены, получим

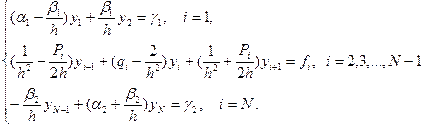(1.22)

Пример1. Методом конечных разностей решить краевую задачу

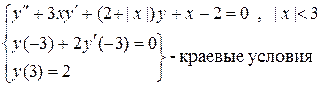
В этом случае

, ,

; ; ,

, , , , , .

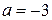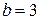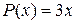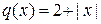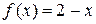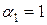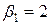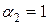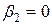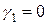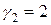Пример М-файла

function krz_odu2

a=input('ввести координату левого конца отрезка a=');

b=input('ввести координату правого конца отрезка b=');

al1=input('ввести параметр alfa1='); bt1=input('ввести параметр beta1=');

gm1=input('ввести параметр gamma1=');

al2=input('ввести параметр alfa2='); bt2=input('ввести параметр beta2=');

gm2=input('ввести параметр gamma2=');

n=input('ввести число точек n=');

l=b-a; h=l/(n-1); xi=(a:h:b)'; x=xi(2:n-1);

P=3*x;

q=2+abs(x);

f=2-x;

tm=1/h^2-P/(2*h);

t0=q-2/h^2;

tp=1/h^2+P/(2*h);

A=diag([tm;-bt2/h],-1)+diag([al1-bt1/h;t0;al2+bt2/h])+diag([bt1/h;tp],1);

disp('матрица системы разностных уравнений'),disp(A)

b=[gm1;f;gm2];

disp('вектор правой части системы разностных уравнений'),disp(b)

y=A\b;

disp('решение:'),disp(y)

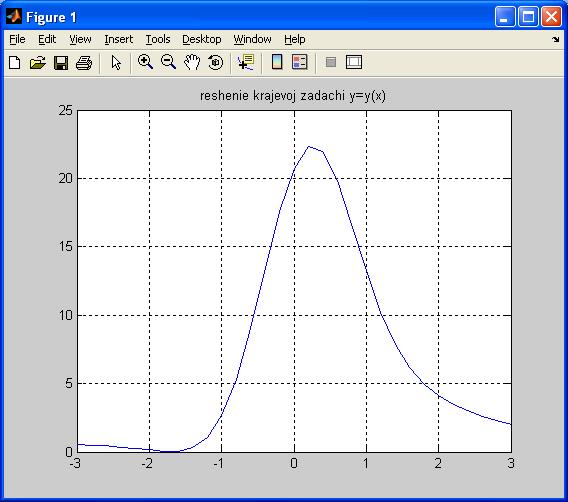
plot(xi,y),grid on,title('reshenie krajevoj zadachi y=y(x)')

Результаты решения при n=9

ввести координату левого конца отрезка a=-3

ввести координату правого конца отрезка b=3

ввести параметр alfa1=1

ввести параметр beta1=2

ввести параметр gamma1=0

ввести параметр alfa2=1

ввести параметр beta2=0

ввести параметр gamma2=2

ввести число точек n=9

матрица системы разностных уравнений

-1.67 2.67 0 0 0 0 0 0 0

6.28 0.69 -2.72 0 0 0 0 0 0

0 4.78 -0.06 -1.22 0 0 0 0 0

0 0 3.28 -0.81 0.28 0 0 0 0

0 0 0 1.78 -1.56 1.78 0 0 0

0 0 0 0 0.28 -0.81 3.28 0 0

0 0 0 0 0 -1.22 -0.06 4.78 0

0 0 0 0 0 0 -2.72 0.69 6.28

0 0 0 0 0 0 0 0 1.00

вектор правой части системы разностных уравнений

4.25

3.5

2.75

1.25

0.5

-0.25

решение:

-1.0629

-0.66432

-4.1819

-5.2704

43.962

44.862

7.6812

11.67

>>

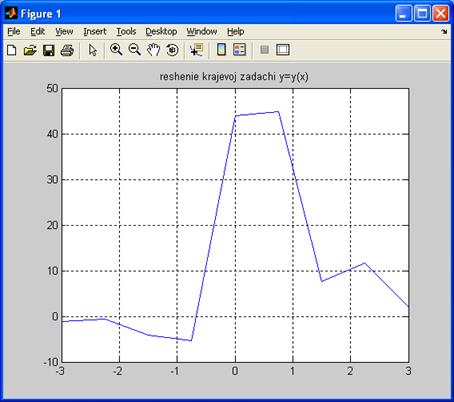
Результаты решения при n=17

ввести координату левого конца отрезка a=-3

ввести координату правого конца отрезка b=3

ввести параметр alfa1=1

ввести параметр beta1=2

ввести параметр gamma1=0

ввести параметр alfa2=1

ввести параметр beta2=0

ввести параметр gamma2=2

ввести число точек n=17

матрица системы разностных уравнений

………………………………………………

вектор правой части системы разностных уравнений

…………………………………………………………..

решение:

0.58

0.47

0.32

0.09

-0.14

0.81

5.26

13.34

20.52

22.21

17.38

10.81

6.50

4.44

3.32

2.56

2.00

>>

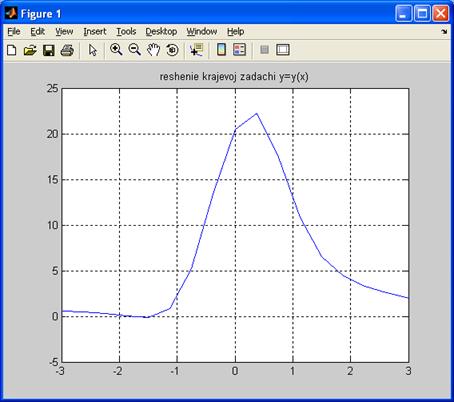
Результаты решения при n=31

ввести координату левого конца отрезка a=-3

ввести координату правого конца отрезка b=3

ввести параметр alfa1=1

ввести параметр beta1=2

ввести параметр gamma1=0

ввести параметр alfa2=1

ввести параметр beta2=0

ввести параметр gamma2=2

ввести число точек n=31

матрица системы разностных уравнений

………………………………………………

вектор правой части системы разностных уравнений

…………………………………………………………..

решение:

0.57

0.51

0.44

0.36

0.27

0.16

0.07

0.06

0.30

1.06

2.65

5.33

9.06

13.41

17.60

20.76

22.34

21.95

19.83

16.65

13.24

10.21

7.85

6.15

4.96

4.12

3.50

3.01

2.62

2.28

2.00

>>

Пример 2. Решить краевую задачу методом конечных разностей.

; ; ; ,

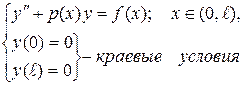
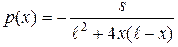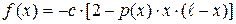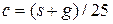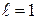где 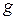– номер группы; 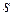– номер студента по журналу.

В этом случае

, ,

; ; ,

, , , , , .

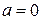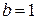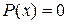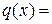
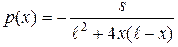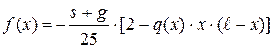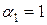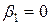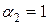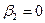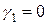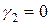Пример М-файла (для случая s=12, g=3)

a=input('ввести координату левого конца отрезка a=');

b=input('ввести координату правого конца отрезка b=');

al1=input('ввести параметр alfa1='); bt1=input('ввести параметр beta1=');

gm1=input('ввести параметр gamma1=');

al2=input('ввести параметр alfa2='); bt2=input('ввести параметр beta2=');

gm2=input('ввести параметр gamma2=');

n=input('ввести число точек n=');

l=b-a; h=l/(n-1); xi=(a:h:b)'; x=xi(2:n-1);

s=12;g=3;

P=zeros(n-2,1);

q=-s./(l^2+4*x.*(l-x));

f=-(s+g)/25*(2-q.*x.*(l-x));

tm=1/h^2-P/(2*h);

t0=q-2/h^2;

tp=1/h^2+P/(2*h);

A=diag([tm;-bt2/h],-1)+diag([al1-bt1/h;t0;al2+bt2/h])+diag([bt1/h;tp],1);

disp('матрица системы разностных уравнений'),disp(A)

b=[gm1;f;gm2];

disp('вектор правой части системы разностных уравнений'),disp(b)

y=A\b;

disp('решение:'),disp(y)

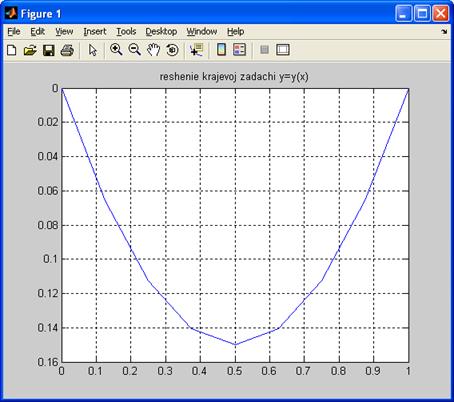
plot(xi,y),grid on,title('reshenie krajevoj zadachi y=y(x)')

Результаты решения при n=9

ввести координату левого конца отрезка a=0

ввести координату правого конца отрезка b=1

ввести параметр alfa1=1

ввести параметр beta1=0

ввести параметр gamma1=0

ввести параметр alfa2=1

ввести параметр beta2=0

ввести параметр gamma2=0

ввести число точек n=9

матрица системы разностных уравнений

1.0000 0 0 0 0 0 0 0 0

64.0000 -136.3478 64.0000 0 0 0 0 0 0

0 64.0000 -134.8571 64.0000 0 0 0 0 0

0 0 64.0000 -134.1935 64.0000 0 0 0 0

0 0 0 64.0000 -134.0000 64.0000 0 0 0

0 0 0 0 64.0000 -134.1935 64.0000 0 0

0 0 0 0 0 64.0000 -134.8571 64.0000 0

0 0 0 0 0 0 64.0000 -136.3478 64.0000

0 0 0 0 0 0 0 0 1.0000

вектор правой части системы разностных уравнений

-1.7478

-1.9714

-2.0710

-2.1000

-2.0710

-1.9714

-1.7478

решение:

0.0000

0.0656

0.1125

0.1406

0.1500

0.1406

0.1125

0.0656

>>