Независимость аксиом Пеано.
Множество натуральных чисел.
Определение. Натуральными числами назовем элементы множества N, в котором выделен элемент  и определено отображение
и определено отображение 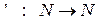 (
( 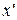 -следующий за
-следующий за  , удовлетворяющее следующим аксиомам:
, удовлетворяющее следующим аксиомам:
1. 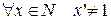 (1 не следует ни за каким натуральным числом);
(1 не следует ни за каким натуральным числом);
2. 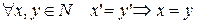 (инъективность);
(инъективность);
3.  .
.
Аксиомы 1-3 будем называть аксиомами Пеано.
Следствия из аксиом Пеано:
1) 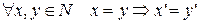 (однозначность).
(однозначность).
2)  .
.
Доказательство. Предположим, что 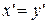 . Тогда, по аксиоме 2,
. Тогда, по аксиоме 2,  . Поучили противоречие с условием
. Поучили противоречие с условием  , следовательно, предположение ложно.
, следовательно, предположение ложно.
3)  .
.
Доказательство. Пусть  .
. 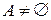 , т.к.
, т.к. 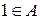 . Покажем, что
. Покажем, что 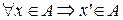 .
.  . Тогда, по 3 аксиоме Пеано,
. Тогда, по 3 аксиоме Пеано,  .
.
4) 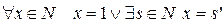 .
.
Доказательство. Пусть  .
. 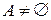 , т.к.
, т.к. 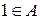 . Покажем, что
. Покажем, что 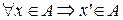 .
. 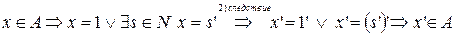 . Тогда, по 3 аксиоме Пеано,
. Тогда, по 3 аксиоме Пеано,  .
.
5) І форма метода математической индукции для множества натуральных чисел: Если утверждение 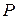 о натуральных числах верно для 1 и из истинности этого утверждения для всякого числа
о натуральных числах верно для 1 и из истинности этого утверждения для всякого числа  следует истинность его для
следует истинность его для 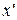 , то
, то 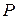 справедливо для каждого натурального числа.
справедливо для каждого натурального числа.
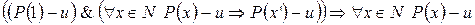 .
.
Доказательство. Пусть 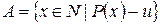 .
. 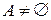 , т.к.
, т.к. 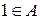 . Из условия теоремы имеем, что
. Из условия теоремы имеем, что 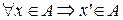 . Тогда, по 3 аксиоме Пеано,
. Тогда, по 3 аксиоме Пеано,  .
.
Независимость аксиом Пеано.
 Для доказательства независимости каких-либо двух аксиом от третьей достаточно построить модель теории, в которой указанные две выполняются, а третья – нет.
Для доказательства независимости каких-либо двух аксиом от третьей достаточно построить модель теории, в которой указанные две выполняются, а третья – нет.
Доказательство.
Построим модель теории, в которой
1) выполняются аксиомы 2 и 3, а 1-нет.
Очевидно, что 1 аксиома не выполняется, т.к. 1 следует за 1''.
2) выполняются аксиомы 1 и 3, а 2-нет.
Аксиома 2 не выполняется, т.к. 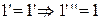 .
.

3) выполняются аксиомы 1 и 2, а 3-нет.
 Аксиома 3 не выполняется, т.к.
Аксиома 3 не выполняется, т.к.
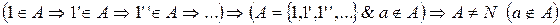 .
.
Дата добавления: 2022-04-12; просмотров: 264;











