Розподілювачі імпульсів. Лічильника Джонсона
Розподілювачами називають функціональні вузли, які циклічно розподіляють потік імпульсів по декількох каналах. Прикладом розподілювача може служити схема двійкового лічильника, на вхід якого подаються імпульси для підрахунку, а виходи приєднані до дешифратора. Збільшуваний або зменшуваний вихідний двійковий код лічильника дешифрується дешифратором по ряду каналів, створюючи в кожному з них послідовність імпульсів, що задається циклом роботи схеми. Аналіз такої схеми без урахування динамічних процесів показує, що створювані імпульсні послідовності можуть бути симетричними, якщо лічильник має модуль 2m. Якщо ж модуль перерахунку не відповідає такій кратності, то не всі вихідні послідовності матимуть симетричний вид. При врахуванні динамічних режимів перемикання лічильника на виході дешифратора виникають короткі сплески напруги – гонки, які ще більше спотворюють вихідні послідовності.
Функцію розподілювача може виконувати цифровий автомат, що складається з послідовно з’єднаних тригерів, якщо лише в один його тригер помістити одиничний сигнал. При подачі синхроімпульсів записана одиниця переміщуватиметься по іншим тригерам (розрядам), відображаючи на лінійній шкалі кількість поданих синхроімпульсів (наприклад, загоряння лампочки номеру поверху в ліфті). Значно більші можливості мають цифрові автомати, що мають зворотний зв’язок з виходів на вхід. У літературі такі схеми, у залежності від характеру зворотних зв’язків, називають кільцевими лічильниками, лічильниками Джонсона, лічильниками Мебіуса, лічильниками в коді Лібау-Крейга, кільцями Реженера.
Загальна структура кільцевого лічильника приведена на рис. 8.13.
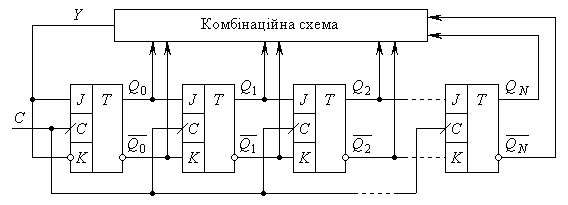
Рис.8.13.
Особливість її полягає в тому, що допоміжно вона має комбінаційну схему, яка обробляє вихідні сигнали кожного тригера і генерує черговий сигнал на вхід автомата:
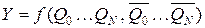 .
.
Тому можемо взаємозв’язок між входами/виходами кожного розряду зобразити у вигляді систем рівнянь:
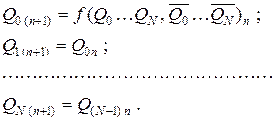
Ланка зворотного зв’язку формує сигнал 0 або1, задаючи тим самим черговий стан схем лічильника.
У загальному плані аналіз таких схем досить складний, тому розглянемо ряд конкретних широко використовуваних схем лічильників. Найпростіший варіант зворотного зв’язку має схема кільцевого лічильника, в якій виходи тригера старших розрядів безпосередньо з’єднані з входами тригера молодших розрядів (рис. 8.14).
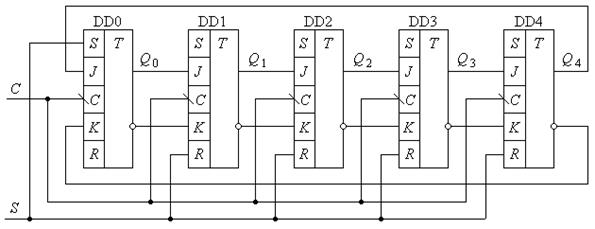
Рис.8.14.
Схема доповнена входом сигналу початкової установки S, високий рівень на якому встановлює тригер DD0 в одиничний стан, а решту – в нульовий. Часова діаграма лічильника при подачі серії синхроімпульсів матиме вигляд, приведений на рис.8.15. Записана в DD0 одиниця переміщується в черговий розряд (старший або молодший у залежності від напрямку зсуву) і затримується в ньому на інтервал часу, що дорівнює періоду синхроімпульсу TC . Решта тригерів знаходиться в нульовому стані.
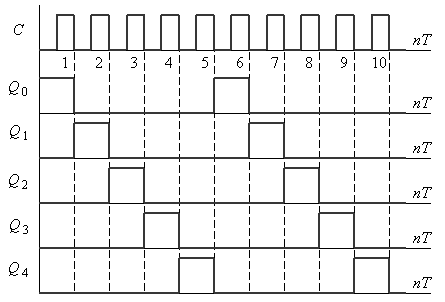
Рис.8.15.
Слід враховувати, що при вмиканні живлення тригери можуть встановлюватись довільним шляхом, тому необхідно мати можливість попередньої установки лічильника по входу S.
Розглянута схема може повністю замінити описану вище пару “двійковий лічильник - дешифратор” при перетворенні кількості вхідних імпульсів у код, що задається кількістю тригерів. Вихідна частота імпульсів по будь-якому з виходів дорівнює 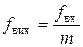 , де m – кількість тригерів. Оскільки в схемі, що розглядається, відсутні зовнішні логічні елементи, то кільцеві лічильники мають високу швидкодію. Але одним з недоліків кільцевих лічильників є велика кількість використовуваних тригерів.
, де m – кількість тригерів. Оскільки в схемі, що розглядається, відсутні зовнішні логічні елементи, то кільцеві лічильники мають високу швидкодію. Але одним з недоліків кільцевих лічильників є велика кількість використовуваних тригерів.
Розглянута схема має досить широке використання. Так вона може виконувати функцію розподілення імпульсів по декількох каналах, кількість яких рівна m.
Функції розподілення широко використовуються в керуванні пристроями енергетичної електроніки, керування кроковими двигунами. За допомогою кільцевих лічильників і допоміжної логіки можна створювати пристрої автоматичного формування сигналів тривоги, оповіщення і т. п.
Недолік кільцевого лічильника, обумовлений великою кількістю тригерів, необхідних для реалізації необхідного коефіцієнта перерахунку, може бути усунений, якщо один із зв’язків між тригерами зробити перехресним, тобто вхід одного з тригерів з’єднати з інверсним виходом попереднього. При цьому принципово не має значення той факт, між якими з тригерів установлений перехресний зв’язок (лічильник Мебіуса).
Після установки всіх тригерів у нульовий стан на вході першого тригера матимемо сигнал логічної одиниці, який з кожним синхроімпульсом передаватиметься вправо, не зникаючи в попередньому розряді до заповнення всіх розрядів. За рахунок зворотного зв’язку у наступному циклі по лічильнику нарощуватиметься кількість нулів.
На рис. 8.16 приводиться приклад такого десяткового лічильника, що має п’ять тригерів.

Рис. 8.16
Прийнявши, що в нульовому стані всі тригери лічильника встановлюються в нуль, отримаємо послідовність відліку, що приводиться у табл. 8.3.
Таблиця 8.3.

Отримана послідовність має 10 станів, які можна вибрати з табл. 8.3. Логічна схема ланки зворотного зв’язку DO може бути отримана таким чином: у стовпець таблиці DO заносяться необхідні значення сигналу DO для забезпечення послідуючого стану.
В результаті отримуємо:
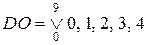 .
.
Переходячи до логічних змінних Q0…Q4 й мінімізуючи їх за допомогою карт Карно (рис. 8.17), отримуємо:
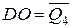 ,
,
що підтверджує відповідність схеми рис. 8.16 і табл. 8.3.
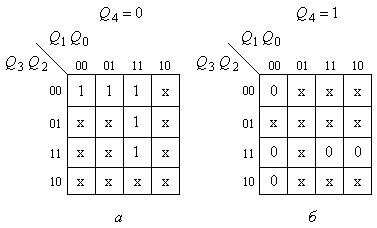
Рис. 8.17.
Організація десяткового відліку може бути забезпечена допоміжною логікою, яка призначена для декодування станів лічильника. Для визначення і мінімізації логіки декодування станів карти Карно, що зображені на рис. 8.17, дещо змінимо, вписавши до них номери станів (рис. 8.18).
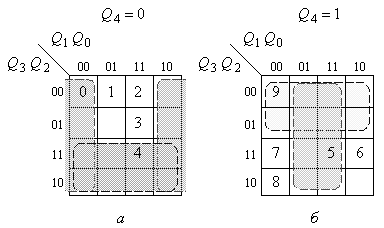
Рис. 8.18.
Використовуючи відомі засоби мінімізації, для функцій, що залежить від Q4 , маємо:

Аналогічно отримуються і функції, які не залежать від Q4 . Результати мінімізації представлені у табл. 8.3.
Для лічильника Джонсона, що розглядається, існують також три послідовності, відповідно до яких він може змінювати свої стани після дії перешкод:
1. S2 → S5 → S11 → S23 → S14 → S29 → S26 → S20 → S8 → S17 → S2 ;
2. S4 → S9 → S19 → S6 → S13 → S27 → S22 → S12 → S25 → S18 → S4 ;
3. S10 → S21 → S10 .
Вказані послідовності можуть бути відображені за допомогою карт Карно (рис. 8.19), цифри на яких відповідають вказаним послідовностям.
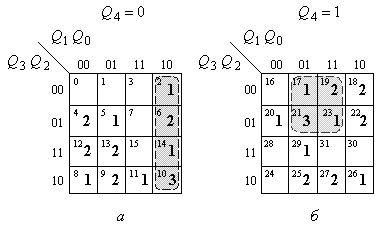
Рис. 8.19.
З карти, що приведена на рис. 8.19, а, бачимо, що чотири суміжні клітини зі станами S2 , S6 , S14 , S10 охоплюють стани всіх небажаних послідовностей. Такою ж групою клітин на рис. 8.19, б є клітки з номерами S17 , S19 , S21 , S23 . Функції, що описують ці групи кліток, мають вигляд:
 .
.
Є і інші варіанти таких функцій. Якщо використати одну з таких функцій для установки всіх тригерів, то через один цикл роботи лічильник відновить правильну послідовність зміни станів.
Лічильник Джонсона має парну довжину циклу відліку, яка дорівнює 2m. Але, як ми бачили з аналізу роботи лічильника і табл. 8.3, можна змінити функцію зворотного зв’язку з тим, щоб зменшити величину коефіцієнта перерахунку – наприклад, зробити її непарною. Такі задачі читачам пропонується розв’язати самостійно.
Приклад типової задачі. Знайти таку функцію зворотного зв’язку DO, щоб лічильник не мав станів 00000 і 11111.
Деякі мікросхеми лічильників побудовані на основі схеми Джонсона (наприклад, 564ИE8, 564ИE9).
На рис. 8.20 приводиться функціональна схема одного з таких лічильників, в якому функція зворотного зв’язку має вигляд:
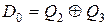 .
.
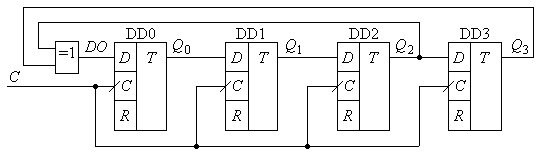
Рис.8.20.
Розглянемо особливості роботи лічильника. Оскільки на вхід DO не поступатимуть інформаційні сигнали при Q3 Q2 Q1 Q0 = 0000 = S0 , то задамо початкову умову:
Q3 Q2 Q1 Q0 = 0001 = S1 .
У цьому випадку
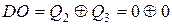
і при появі тактового імпульсу отримаємо новий стан 0010 = S2 .
У табл. 8.4 приведена послідовність зміни станів протягом одного циклу. У циклі маємо 15 різних станів, за винятком стану S0 = 0000, при якому лічильник є непрацездатним. Тобто максимальна довжина послідовності станів lд = 2m – 1. Послідовність максимальної довжини(ПМД) є однією з характеристик лічильника, що розглядається. Тільки конкретно визначені зв’язки функції зворотного зв’язку можуть дати ПМД.
Таблиця 8.4.
| Номер тактового імпульсу | S | Q3 | Q2 | Q1 | Q0 | DO |
| S1 | ||||||
| S2 | ||||||
| S4 | ||||||
| S9 | ||||||
| S3 | ||||||
| S6 | ||||||
| S4 | ||||||
| S10 | ||||||
| S5 | ||||||
| S11 | ||||||
| S7 | ||||||
| S15 | ||||||
| S14 | ||||||
| S12 | ||||||
| S8 | ||||||
| S1 |
Приклад типової задачі. Визначити максимальну довжину циклу, якщо в схемі, приведеній на рис. 8.20, одним з входів суматора за модулем 2 взяти не Q2 , а Q1 . Побудувати таблицю станів.
У табл. 8.5 ПМД приводяться вирази для функції зворотного зв’язку, використання яких дозволяє сформувати ПМД для деяких лічильників з кількістю розрядів від 1 до 18 [Голдсуорт].
Таблиця 8.5.
| Кількість розрядів m | Рівняння зворотного зв’язку |
| Q0 | |
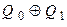
| |

| |
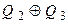
| |
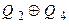
| |
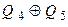
| |
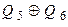
| |
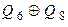
| |
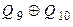
| |
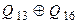
| |
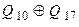
|
Можливо також створити інші ПМД, використовуючи не тільки двовходові логічні елементи ВИКЛ. АБО, а й ЛЕ з більшою кількістю входів.
Дата добавления: 2016-09-26; просмотров: 2623;











