Линейные пространства

Модуль над кольцом, пространство над полем.

Определение. Пусть 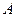- абелева группа по сложению, 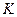- кольцо.

Если задана операция внешнего умножения 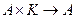, удовлетворяющая свойствам: :

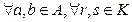1) .

2) 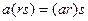(ассоциативность)

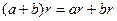3а) 3б) . (дистрибутивность)

То 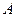называется модулем над кольцом 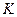и обозначается 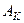(правый 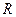-модуль).

В том случае, когда не просто кольцо, а поле, модуль называется пространством над .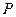

Определение.Абелева группа 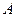называется линейным пространством над полем 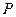, если задана внешняя операция (умножение на константу) 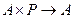, и верны такие свойства для внешней операции умножения :

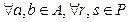1) .

2) 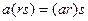(ассоциативность)

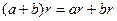3а) 3б) . (дистрибутивность)

Понятие «линейное пространство» более общее, чем «векторное пространство». Примеры: пространство матриц размера , пространство многочленов порядка 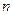, пространство функций. Так, например, функции тоже можно, как и векторы, складывать и умножать на коэффициент, существует тождественно нулевая функция, а для всякой 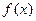существует .

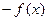Здесь видна граница между алгеброй и геометрией: векторное пространство это геометрическое понятие, а если рассматривать абстрактное множество с похожими свойствами, то уже алгебраическое.

- - - Перерыв - - -

ЛЗС, ЛНС, ранг системы векторов.

Определение.Пусть 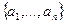- некоторая система элементов линейного пространства. 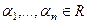- константы. Тогда 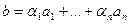называется линейной комбинацией .

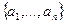(если все коэффициенты = 1, то это просто сумма).

Чаще всего мы будем формулировать в терминах векторов.

Пример. 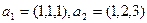. Пусть коэффициенты 2 и 1. Линейная комбинация это вектор (3,4,5): 2(1,1,1)+1(1,2,3) = (3,4,5).

В пространстве, рассмотрим 3 вектора: (1,0,0), (0,1,0) и (0,0,1). Любой вектор 3-мерного пространства можно представить как линейную комбинацию этих трёх векторов.

* Если все коэффициенты 0, то линейная комбинация есть 0 вектор в любом случае, какими бы ни были векторы.

* Рассмотрим векторы (1,0) и (-1,0). Если их сложить, то получим (0,0). Видим, что бывают ситуации, когда линейная комбинация ненулевых векторов - это нулевой вектор, даже если ненулевые коэффициенты! Аналогичная ситуация, если вектор с есть a+b, тогда a+b-c = 0. В связи с этим возникает определение линейно-зависимой и линейно-независимой системы векторов.

Определение.Если из равенства 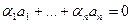следует, что 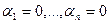, то система векторов называется линейно-независимой системой (ЛНС). Если же существует набор ненулевых коэффициентов 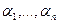, такой, что линейная комбинация = 0, то система называется линейно-зависимой системой (ЛЗС).

Примеры.

* Если вектор с есть a+b, тогда a+b-c = 0. Коэффициенты 1,1,-1.

* если 2 вектора коллинеарны, то они образуют ЛЗС.

* Система, состоящая из одного ненулевого вектора, ЛНС.

(чтобы при умножении его на число был 0-вектор, требуется 0 константа).

Теорема.Система линейно зависима 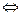хотя бы один из векторов этой системы является линейной комбинацией остальных.

Доказательство.

Необходимость. Если система ЛЗС, то 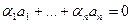, при этом хотя бы при каком-то векторе ненулевой коэффициент, тогда это слагаемое можно перенести в другую сторону и разделить всё равенство на этот коэффициент. Для определённости, например, пусть это будет n-й коэффициент. Тогда

, и 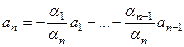, последний вектор выражен через остальные.

Достаточность. Если какой-то вектор выражен через остальные, его можно перенести в другую сторону равенства, ко всем остальным векторам, то есть в записи 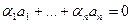ему будет соответствовать коэффициент (-1).

Так, если выражен 1-й вектор, то 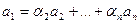, тогда 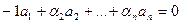. Получается, что ненулевой набор коэффициентов есть, а значит, система ЛЗС.

Лемма.Если система векторов содержит вектор , то она ЛЗС.

Докажем этот факт. Коэффициент при 0-векторе может быть любым числом, т.к. он всё равно не влияет на сумму векторов, а значит, существует набор коэффициентов, в котором не все нули, и значит, формально по определению такая система векторов ЛЗС.

Лемма.

1. Если подсистема ЛЗС, то система ЛЗС.

2. Если система ЛНС, то подсистема ЛНС.

Доказательство.Пусть подсистема из 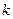векторов линейно - зависима, то есть равенство 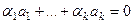, где 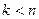, выполняется при некоторым наборе коэффициентов, отличных от нуля. Тогда в системе из 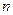векторов также получится, что такое равенство выполняется при некотором ненулевом наборе коэффициентов, ведь даже если все после номера k сделать нулевыми, то в левой части остаются ненулевые.

.

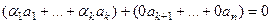Пункт 2 следует из 1 логически, т.к. если система ЛНС и допустить, что её подсистема ЛЗС, то по п.1. вся система ЛЗС.

Определение. Максимальная линейно-независимая подсистема называется базисом системы векторов, а число векторов в ней - рангом системы векторов.

Примеры.

1. Если в плоскости есть 2 неколлинеарных вектора, и добавлены 10 векторов в той же плоскости, всё равно .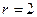

2. Если 3 вектора, из которых 2 коллинеарны. Ранг = 2.

3. Если 3 вектора, все 3 коллинеарны. Ранг = 1.

4. Если 2 вектора на оси , третий нет. Базис можно составить

из 1-го и 3-го а также 2-го и 3-го. Базис не единственный.

Определение. Максимальная линейно-независимая система векторов линейного пространства называется базисом пространства, а число векторов (или иных элементов), из которых она состоит - размерностью пространства.

Теорема. Всякий вектор n-мерного пространства можно, причём единственным образом, представить в виде линейной комбинации векторов базиса.

Доказательство.Пусть 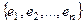- базис. Так как пространство n-мерно, то при добавлении в систему ещё одного вектора , система становится линейно-зависимой:

ЛЗС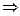

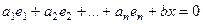
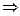
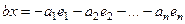на коэффициент 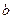можно поделить, т.к. он отличен от 0, иначе было бы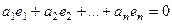

и тогда система 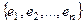сама была бы ЛЗС.

Итак, 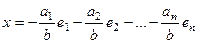, вектор выражен через базис.

Единственность.

Пусть существует 2 различных разложения по базису.

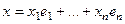и . Тогда

, причём не все разности равны 0.

Тогда система векторов 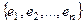линейно-зависима, что противоречит тому, что она образует базис.

Итак, теорема доказана.

Определение. Коэффициенты линейного разложения вектора по базису будем называть координатами вектора относительно данного базиса.

Лекция 4

ГЛАВА 2. Матрицы.

Перестановки.

Перестановки. Транспозиции. Изменение чётности.

Расположение первых n натуральных чисел 1,2,3,..., n в некотором порядке называется перестановкой из n чисел.

Теорема.Существует n! перестановок порядка n.

Доказательство.Для n = 2 это очевидно, перестановки только (12) и (21). Дальше, доказательство по индукции. Пусть теперь для (n-1) этот факт доказан. Рассмотрим для n. На первом месте может стоять любое из n чисел, и при каждой из этих ситуаций, остаётся (n-1) число, которые должны занять (n-1) место, а это возможно (n-1)! способами. Итак, получается 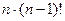что как раз равно n!, что и требовалось доказать.

В частности, при n = 3 получается 6 перестановок:

(123) (132) (213) (231) (312) (321)

На первом месте одно из 3 чисел, и при этом оставшиеся 2 числа можно расставить на 2 места двумя способами. Получается 6 способов. Заметим, что 3! = 6.

Определение.Пусть - некоторая перестановка из n чисел. Говорят, что пара 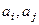образует инверсию, если , .

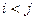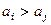Если число всех инверсий чётное, перестановка называется чётной, если нечётное - то нечётной.

Пример: всего 2 инверсии.

6 инверсий:

Переход от перестановки 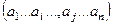к 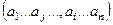(поменять элементы на местах i и j ) называется транспозицией.

Теорема.Транспозиция меняет чётность перестановки.

Доказательство.

1. Пусть 2 элемента, которые будем менять, расположены на соседних местах. Тогда при смене их порядка, одна инверсия или появляется, или напротив, исчезает. При этом относительно любого другого числа, если какое-то из них образовывало инверсию, то она так и остаётся (оно как было левее/правее этого блока, так и останется).

2. Общий случай. Пусть теперь 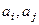расположены на произвольных местах. Чтобы поменять их местами, можно выполнить такие транспозиций: поменять 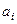с соседним справа 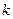раз ( 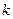- сколько чисел было между ними, 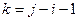, например, между 1-м и 3-м одно место). После этого 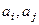окажутся соседними. Затем поменять их, затем 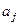менять 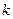раз с соседними слева, пока оно не окажется на том месте, где было 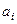. Итого, действий раз изменят чётность, а так как нечётное число, то в итоге чётность поменяется.