Філософи, що обідають

Класичною вже стала неформальна постановка завдання розподілу ресурсів, що носить назву "Проблеми філософів, що обідають," і показана на Малюнку 5.1.

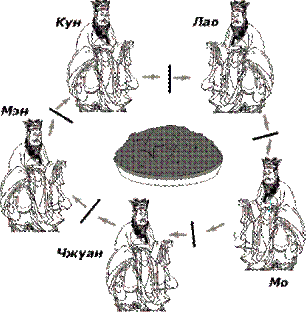Ріс.5.1. Філософи, що обідають. Безвихідь

П'ять філософів сидять за круглим столом, в центрі якого коштує блюдо з рисом. Між кожною парою філософів лежить паличка для їжі, паличок, отже, теж п'ять. Для того, щоб почати є, філософ повинен узяти дві палички - зліва і праворуч від себе. Таким чином, якщо один з філософів їсть, його сусіди справа і зліва позбавлені такої можливості, оскільки їм бракує палички. Кожен філософ "працює" по зацикленому алгоритму: спочатку він якийсь час думає, потім бере палички і їсть, потім знову думає і так далі Тимчасові інтервали мислення і їжі випадкові, дії філософів, отже, не синхронізовані. Нічого не мовиться в умові про те, яким чином філософ бере палички, - наше завдання якраз і полягає в тому, щоб забезпечити таку стратегію виділення паличок, яка б виключала безвихідь і нескінченне відкладання.

Якщо ми встановимо, що кожен філософ повинен узяти одну паличку і не випускати її з рук до тих пір, поки не візьме другу паличку, то ми можемо отримати ситуацію, показану на Ріс.5.1. (стрілка від філософа до палички означає, що філософ хоче узяти цю паличку, стрілка у зворотному напрямі - що цю паличку цей філософ вже узяв.) Кожен з філософів узяв паличку праворуч від себе, але не може узяти паличку зліва. Жоден з філософів не може ні є, ні думати. Ця ситуація і називається тупиками (deadlock).

Якщо ж ми встановимо, що філософ повинен узяти обидві палички відразу, то може виникнути ситуація, показана на Ріс.5.2. Філософ Чжуан хоче узяти палички, але виявляє, що його права паличка зайнята філософом Мо. Чжуан чекає. Тим часом філософ Мен бере свої палички і починає є. Мо є закінчує, але Чжуан не може почати є, оскільки тепер зайнята його ліва паличка. Якщо Мо і Мен їдять поперемінно, то Чжуан потрапляє в положення, яке називається голодуванням (starvation) або нескінченним відкладанням.

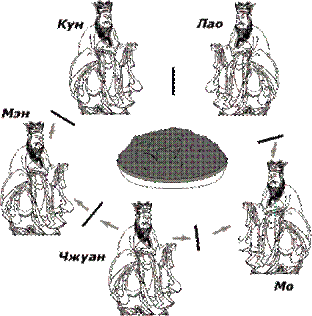Ріс.5.2. Філософи, що обідають. Нескінченне відкладання

Переходячи від філософів до обчислювальних систем, ми можемо проілюструвати безвихідь таким прикладом. Процес A використовує магнітну стрічку, але для завершення йому потрібний ще і принтер. В цей час процес B утримує за собою принтер, але йому потрібна ще магнітна стрічка. Процеси A і B блокують один одного, тобто, знаходяться в тупиків. У системах з множинними ресурсами і з високим рівнем мультипрограмування тупикові ситуації можуть бути і не такими очевидними. Безвихідь може бути локальною і глобальною. Так, якщо у вищенаведеному прикладі рівень мультипрограмування вище 2, то процеси A і B знаходяться в локальній тупиків, інші процеси, яким не потрібні ресурси, зайняті процесами A і B, можуть виконуватися. Філософи ж на Ріс.5.1 знаходяться в глобальній тупиків.

Нескінченне відкладання - ситуація навіть більш загальна, властива управлінню будь-якими ресурсами, а не тільки монопольними. Так, при плануванні процесорного часу по статичних пріоритетах низькопріоритетний процес може відкладатися до безкінечності, якщо в систему постійно поступають процеси з вищими пріоритетами.

Безвихідь є ситуацією небезпечнішу, ніж нескінченне відкладання: процеси, що потрапили в безвихідь, утримують при цьому системні ресурси. Навіть якщо безвихідь не глобальна, система продовжує працювати із зменшеним об'ємом ресурсів, отже, із зниженою продуктивністю. Нескінченне ж відкладання одного або декількох процесів може і не вплинути на середню пропускну спроможність системи, але, звичайно ж, впливає на показники справедливості обслуговування.