МЕРА ОБУСЛОВЛЕННОСТИ

Мерой скаляра служит абсолютное значение. Для сопоставления между собой векторов или матриц вводят понятие нормы вектора или матрицы как соответствующие обобщения абсолютной величины действительного числа.

Норму вектора можно вводить по-разному, но в любом случае она должна обладать некоторыми свойствами.

Пусть имеется n-мерное пространство Rⁿ. Если для любого вектора xÎ Rⁿ существует число ||x|| такое, что:

1) ||x|| ³ 0, причем ||x||=0 только тогда, когда х=0;

2) ||ax|| = |a|×||x||, где aÎR;

3) ||x+y|| £ ||x||+||y|| для любых x, y Î Rⁿ,

то ||x|| называется нормой вектора x= {x₁, x₂,…, x_n}.

В линейной алгебре наиболее часто используются следующие нормы:

а) евклидова норма

,

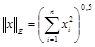которая совпадает с обычным понятием длины вектора;

б) норма Чебышева (sup-норма)

.

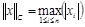Ввести норму для матрицы можно по аналогии с вектором, представив ее в виде «длинного» вектора А={a_ij}={a₁₁ , a₂₁ ,…, a_n1 , a₁₂ , a₂₂ ,…, a_nn} и применяя любую векторную норму к этому «длинному» вектору, например,

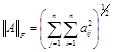– фробениусовская норма в пространстве R^n´n.

При анализе сходимости итерационных методов решения СЛАУ более полезной оказывается другая оценка матриц, связанная с их ролью операторов. Запись СЛАУ в виде Ах=b можно трактовать следующим образом: линейный оператор А переводит вектор х в вектор b. Тогда норма вектора ||Ax|| будет являться величиной образа вектора x при отображении его с помощью оператора А.

Поэтому норма матрицы определяется как максимальная величина, на которую А может растянуть любой вектор в заданной норме ||x||.

.

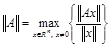Сразу отметим полезное неравенство ||Ax|| £ ||A||×||x||.

В зависимости от применяемой нормы вектора будут получаться различные значения нормы матрицы.

Например, если взять 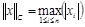, то подчиненная форма матрицы

.

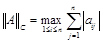Если взять евклидову норму вектора, то

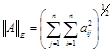
Линейные системы, чьи решения очень чувствительны к изменениям данных в этих системах, называются плохо обусловленными.

Пример 2.Рассмотрим две линейные системы:

;

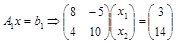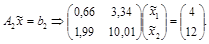
Обе системы имеют решение (1; 1)^Т.

Заменим вектор правой части b₁ на b₁ – (0,04; 0,06)^Т (это соответствует 0,43% -ому изменению этого вектора в евклидовой норме). Тогда новое решение первой системы станет равным (0,9930; 0,9968)^Т; относительное изменение решения составляет 0,51% .

Заменим вектор правой части b₂ на ту же самую величину (это будет соответствовать ее 0,55%-ому относительному изменению). Тогда новое решение второй системы будет равно (6; 0)^Т. Здесь относительное изменение решения равно 324%!

Графический анализ показывает, что уравнения второй системы – две почти параллельные прямые, так что малое смещение какой-либо одной из них существенно сдвигает точку пересечения.

Матрицы коэффициентов при неизвестных в таких смыслах тоже называются плохо обусловленными.

Классический пример плохо обусловленных матриц – матрицы Гильберта:

.

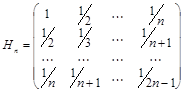С увеличением n эта матрица становится все более плохо обусловленной.

Но графический способ распознавания таких систем прост лишь для n=2. Найдем меру обусловленности линейных систем для любого n [8].

Пусть х_* – вектор решения СЛАУ Ах=b , тогда

Ах_*º b . (4.12)

Пусть коэффициенты и правые части известны с некоторой погрешностью DА и Db соответственно. Определим относительную погрешность решения Dх.

(А+DА)(х_*+ Dх)=b+Db; Ax_* + DAx_* + ADx + DADx = b + Db.

Пренебрегаем слагаемым второго порядка малости DADx и, пользуясь соотношением (4.12), получаем

Dх=A^–1Db – A^–1DAx_* .

Тогда относительная погрешность решения будет равна

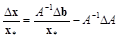
или, после преобразования,

.

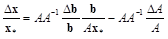Нормируем это выражение:

.

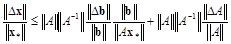Обозначим ||A||×||A^–1||=M_A и воспользуемся тем, что из (4.12) следует ||b|| £ ||A||×||x_*||.

Тогда .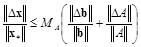

Таким образом, относительное изменение хзависит от суммы относительного изменения данных, умноженной на коэффициент М_А, который называется числом, или мерой обусловленности. Видно, что даже при малых относительных изменений данных изменение решения может быть очень велико – для больших М_А.