ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

3.1. АНСАМБЛЬ РЕАЛИЗАЦИЙ

В отличие от детерминированных сигналов, форму которых мы знаем точно, мгновенные значения случайных сигналов заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью, меньшей единицы. Характеристики таких сигналов являются статистическими, т. е. имеют вероятностный вид.

В радиотехнике существует два основных класса сигналов, нуждающихся в вероятностных описаниях. Во-первых, это шумы — хаотически изменяющиеся во времени электромагнитные колебания, возникающие в разнообразных физических системах из-за беспорядочного движения носителей заряда. Во-вторых, случайными являются все сигналы, несущие информацию, поэтому для описания закономерностей, присущих осмысленным сообщениям, также прибегают к вероятностным моделям.

Математическая модель изменяющегося во времени случайного сигнала называется случайным процессом. По определению, случайный процесс X(t) — это функция особого вида, характеризующаяся тем, что значения, принимаемые ею в любой момент времени t, являются случайными величинами.

Замечание 1

В литературе по радиотехнике термины «случайный сигнал» и «случайный процесс» часто используются как синонимы.

До регистрации (до приема) случайный сигнал следует рассматривать именно как случайный процесс, представляющий собой совокупность (ансамбль) функций Времени x_i (t), подчиняющихся некоторой общей для них статистической закономерности. Одна из этих функций, ставшая полностью известной после приема сообщения, называется реализацией случайного процесса. Эта реализация является уже не случайной, а детерминированной функцией времени. На рис. 3.1 приведен пример нескольких реализаций случайного процесса.

Для анализа свойств и характеристик случайного процесса, а также различных его преобразований, необходимо задать математическую модель случайного процесса. Такая модель может представлять собой описание возможных реализаций случайного процесса в сочетании с указанием относительной частоты их появления. Приведем несколько примеров моделей случайных процессов, задаваемых таким образом.

Пример 1. Гармонический сигнал со случайной начальной фазой. Во многих практических задачах используется модель случайного процесса, реализации которого представляют собой гармонические колебания с известными (детерминированными) амплитудой и частотой, но случайной начальной фазой. Таким образом, реализация рассматриваемого случайного процесса может быть записана как

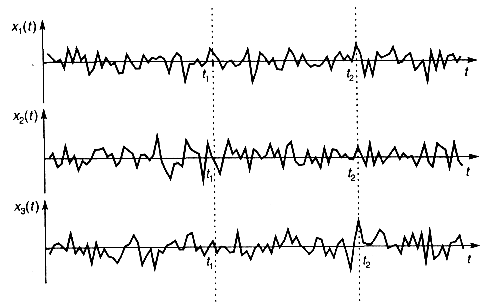
Рис. 3.1. Реализации случайного процесса

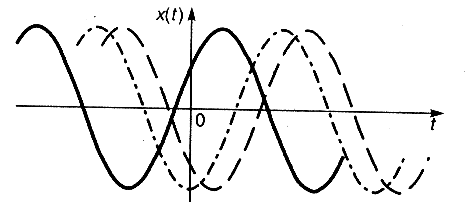
Рис. 3.2. Реализации гармонического сигнала со случайной начальной фазой

где А — амплитуда (детерминированная), ω₀ — частота (детерминированная), и φ — случайная начальная фаза, которая в большинстве практически интересных случаев может считаться равномерно распределенной на интервале О...2π, т. е. имеющей следующую плотность вероятности:

Графики нескольких реализаций данного случайного процесса, представляющие собой смещенные друг относительно друга по временной оси синусоиды, показаны на рис. 3.2.

Как видим, конкретный вид реализации процесса в данном случае определяется значением всего лишь одной случайной величины — начальной фазы.

Замечание 2

Случайные процессы, конкретный вид реализаций которых определяется значениями конечного числа параметров (случайных величин), иногда называют квазидетерминированными случайными процессами.

Пример 2. Сигнал с амплитудно-импульсной модуляцией. При использовании амплитудно-импульсной модуляции (АИМ) сигнал представляет собой сумму сдвинутых по времени импульсов известной формы s₀(t), амплитуды которых α_k являются случайными и определяют передаваемую полезную информацию:

Рис. 3.3. Реализация АИМ-сигнала (а) и формирующий импульс (б)

где Т— временной сдвиг между последовательными импульсами (рис. 3.3).

Замечание 3

На рис. 3.3 для большей наглядности импульсы изображены неперекрывающимися. В реальных системах связи отдельные импульсы могут перекрываться. Кроме того, множители α_k могут быть в том числе и отрицательными, так что использование в данном случае термина «амплитуда» является условным.

В этом примере реализация задается в общем случае бесконечным, но счетным множеством случайных величин α_k.

Замечание 4

Сами коэффициенты α_k образуют дискретный случайный процесс; речь о таких процессах пойдет в § 6.15.

Пример 3. Случайный телеграфный сигнал [11]. Таким сигналом называют случайный процесс, реализации которого принимают значения +1 и — 1, причем перепады уровня происходят в случайные моменты времени и число N перепадов уровня, происходящих за время τ, является случайной величиной с дискретным распределением вероятности, описывающимся законом Пуассона:

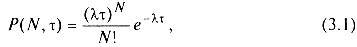
где λ — неотрицательный параметр, определяющий среднюю частоту возникновения перепадов уровня.

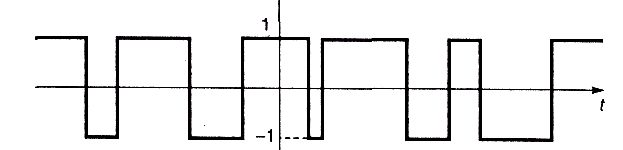
Рис. 3.4. Реализация случайного телеграфного сигнала

Скачки уровня происходят в случайные моменты времени t_k, поэтому аналитически записать формулу для отдельной реализации данного случайного процесса оказывается весьма затруднительно, а изобразить ее график можно лишь условно (рис. 3.4).

В данном случае, как и в предыдущем, конкретная реализация задается бесконечным множеством случайных величин — моментов перепадов уровня t_k, а характеристики случайного процесса определяются статистическими свойствами этих случайных величин.

Итак, полное описание случайного процесса дает его ансамбль реализаций. Однако для решения практических задач часто достаточно более простых характеристик, выражающихся в виде числовых параметров и детерминированных функций. Об этом пойдет речь в следующих параграфах данной главы.

3.2. ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Пусть X(t) — случайный процесс, заданный ансамблем реализаций {x₁(t), X₂(t), ..., x_k(t), ...}. Выбрав произвольный момент времени t₁, зафиксируем значения, принимаемые всеми реализациями:{x₁(t₁), X₂(t₁), ..., x_k(t₁),…} (см. рис. 3.1). Совокупность этих значений образует одномерное сечение случайного процесса и представляет собой случайную величину X(t₁). Напомним кратко основные характеристики случайных величин, отметив при этом, что для одномерных сечений случайных процессов они в общем случае зависят от выбранного момента времени t₁.

Функция распределения вероятности F(x,t₁) равна вероятности того, что в момент времени t­₁ значение случайного процесса не превосходит х:

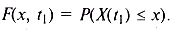
F(x, t₁) является неубывающей функцией, значения которой лежат в диапазоне 0 F(x, t₁) 1. Для предельных значений х выполняются следующие соотношения: F( 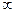, t₁) = 0 и F( 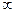, t₁) = 1.

Вероятность попадания значения случайного процесса в интервал (а, b] равна разности значений функции распределения на концах этого интервала:

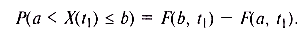
Одномерная плотность вероятности р(х,t₁) представляет собой производную от функции распределения:

Произведение р(х, t₁) dx представляет собой вероятность попадания значения случайного процесса X(t₁) в бесконечно малый интервал шириной dx в окрестности х.

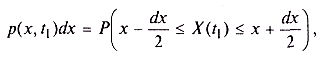
откуда следует, что плотность вероятности является неотрицательной функцией: р(х, t₁) > 0. Чтобы рассчитать вероятность попадания значения X(t₁) в произвольный интервал [а, b], необходимо вычислить следующий интеграл:

Так как случайная величина обязательно принимает какое-нибудь значение, должно выполняться условие нормировки:

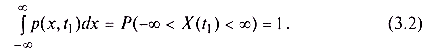
Зная плотность вероятности, можно рассчитать и функцию распределения:

Математическое ожидание и дисперсия. Знание одномерной плотности вероятности р(х, t₁) позволяет произвести статистическое усреднение как самой величины X(t₁), так и любой функции от нее. Под статистическим усреднением подразумевается

усреднение по множеству (по ансамблю реализаций) в каком-либо «сечении» процесса, т. е. в фиксированный момент времени.

Для практических приложений наибольшее значение имеют следующие параметры случайного процесса:

• математическое ожидание, которое служит теоретической оценкой среднего взвешенного значения случайного процесса в момент времени t:

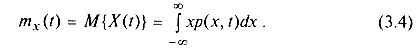
Замечание 1

Во многих практических задачах приходится вычислять математическое ожидание некоторой функции f от случайной величины х, имеющей плотность, вероятности р_x(х). Такое вычисление выполняется по следующей несложной формуле:

Формула для математического ожидания (3.4) является частным случаем (3.5) при f(х) = х.

• дисперсия, характеризующая среднюю мощность отклонений случайного процесса от его среднего значения m_x(t), называемых флуктуациями:

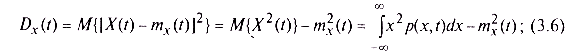
• среднее квадратическое отклонение, представляющее собой квадратный корень из дисперсии и служащее амплитудной мерой разброса значений случайного процесса в момент времени t относительно математического ожидания:

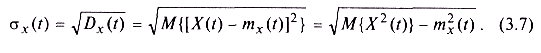
Замечание 2

Дисперсия случайной величины X часто обозначается

как .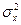

Приведем еще два параметра, связанные с одномерной плотностью вероятности и встречающиеся в некоторых задачах:

• мода представляет собой наивероятнейшее значение случайного процесса в момент времени t, т. е. значение, при котором t достигается максимум плотности вероятности; • медиана представляет собой такое значение случайного процесса в момент времени t, отклонения от которого в любую сторону равновероятны. Математически это можно записать следующим образом:

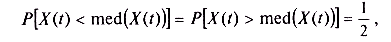
Или

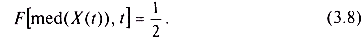
Пример. Проиллюстрируем вычисление различных параметров, связанных с одномерной плотностью вероятности случайной величины, на простом примере.

Пусть случайная величина X имеет плотность вероятности треугольного вида при 0 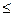х 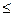1 (рис. 3.5, а). Условие нормировки (3.2) приводит к очевидному выводу: р(1) = 2. Формулу для плотности вероятности можно, таким образом, записать в виде

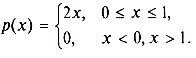
Функция распределения, согласно (3.3), равна интегралу от плотности вероятности (рис. 3.5, б):

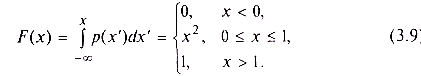
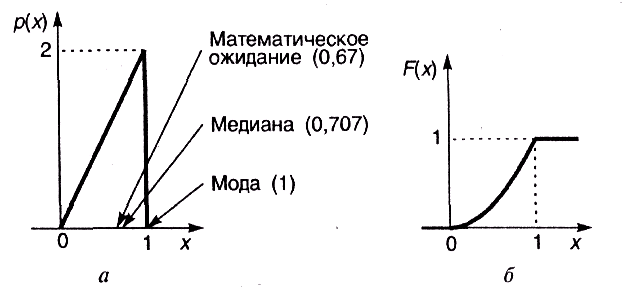
Рис. 3.5. Параметры случайной величины

Рассчитаем параметры такой случайной величины. Математическое ожидание, согласно (3.4), равно

Дисперсия, согласно (3.6), равна

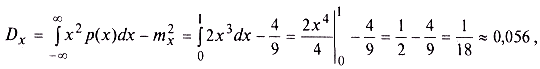
а квадратный корень из полученного числа дает среднее квадратическое отклонение (3.7):

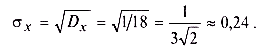
Мода рассматриваемой случайной величины, очевидно, равна 1, так как именно в этой точке плотность вероятности максимальна.

Для нахождения медианы, согласно (3.8) и (3.9), необходимо решить уравнение

отсюда получаем .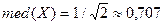

Чтобы проиллюстрировать разницу между понятиями математического ожидания, моды и медианы, соответствующие значения показаны на графике плотности вероятности (см. рис. 3.5, а).

Замечание 3

Если плотность вероятности имеет симметричный вид, то значения математического ожидания и медианы совпадают с центром симметрии.

Замечание 4

Если модель случайного процесса представляет собой описание ансамбля реализаций, подобное примерам, приведенным в § 3.1, то расчет одномерной плотности вероятности случайного процесса сводится к рассмотрению нелинейного преобразования случайных величин-параметров, определяющих вид конкретных реализаций. Нелинейным преобразованиям сигналов в радиотехнических цепях будет посвящена

гл. 7 данного учебного пособия, а речь о нелинейных преобразованиях плотностей вероятности пойдет в § 7.9.

Одномерная плотность вероятности и связанные с ней числовые характеристики позволяют получить важную информацию о свойствах случайного процесса. Однако для решения многих задач таких сведений недостаточно, так как они дают вероятностное представление о случайном процессе X(t) только в отдельные моменты и ничего не говорят о том, как он изменяется во времени.

3.3. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ

СЛУЧАЙНЫХ ПРОЦЕССОВ

Как отмечалось в § 3.2, одномерной плотности вероятности недостаточно для описания поведения случайного процесса во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в произвольные моменты времени t₁ и t₂ (см. рис. 3.1). Совокупность этих двух сечений образует двумерную случайную величину {X(t­1), X(t₂)}, которая описывается двумерной плотностью вероятности р(х­₁, х₂, t­₁, t₂). Произведение р(х₁, х₂, t₁, t₂)dx₁dx₂ представляет собой вероятность того, что реализация случайного процесса X(t) в момент времени t₁ попадает в бесконечно малый интервал шириной dx₁ в окрестности х₁, а в момент времени t₂ — в бесконечно малый интервал шириной dx₂ в окрестности х₂:

Естественным обобщением является n-мерное сечение случайного процесса, приводящее к n-мерной плотности вероятности р{х₁, х₂, ..., х_n, t₁, t₂, ..., t_n). При 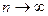такая функция является исчерпывающей вероятностной характеристикой случайного процесса.

По аналогии с одномерным случаем можно ввести многомерную функцию распределения F(x₁, х₂, ..., х_n, t₁, t₂, …, t_n), равную вероятности того, что значения случайного процесса X(t) во все моменты времени t_i не превосходят х_i,:

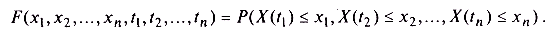
Многомерная функция распределения может быть найдена интегрированием плотности вероятности:

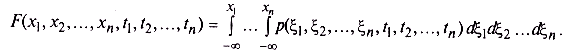
Так же, как и одномерная, многомерная плотность вероятности должна быть неотрицательна, а условие нормировки приобретает следующий вид:

Зная n-мерную плотность, всегда можно найти n-мерную плотность при m < n путем интегрирования по «лишним» координатам:

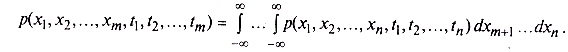
Описание свойств случайных процессов с помощью многомерных плотностей вероятности высокой размерности может быть весьма подробным, однако на этом пути часто встречаются серьезные математические трудности. К счастью, многие задачи, связанные с описанием случайных сигналов, удается решить на основе двумерной плотности вероятности.

В частности, задание двумерной плотности вероятности р(x₁, x₂, t₁, t₂) позволяет определить важную характеристику случайного процесса — его ковариационную функцию

Согласно этому определению ковариационная функция случайного процесса X(t) представляет собой статистически усредненное произведение значений случайной функции X(t) в моменты времени t₁ и t₂.

Для каждой реализации случайного процесса произведение x(t₁)x(t₂) является некоторым числом. Совокупность реализаций образует множество случайных чисел, распределение которых характеризуется двумерной плотностью вероятности р(х₁, х₂, t₁, t₂). Если эта плотность вероятности известна, операция усреднения по множеству осуществляется по формуле

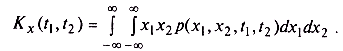
Часто при анализе случайных процессов основной интерес представляет их флуктуационная составляющая. В таких случаях применяется корреляционная функция, представляющая собой статистически усредненное произведение значений центрированной случайной функции X(t) — m_x(t) в моменты времени t₁ и t₂.

Корреляционная функция характеризует степень статистической связи тех значений случайного процесса, которые наблюдаются при t = t₁ и t = t₂. При t₁ = t₂ = t последнее выражение соответствует определению дисперсии случайного процесса X(t). Следовательно, при совмещении сечений функция корреляции равна дисперсии:

Замечание 1

Так сложилось, что в иностранной литературе используется обратная терминология — K_x{t₁, t₂) называется корреляционной, a R_x(t₁, t₂) ковариационной функцией. Во избежание недоразумений об этом следует помнить при работе с зарубежными источниками.

Пример 1. Рассчитаем корреляционную функцию гармонического сигнала со случайной равномерно распределенной начальной фазой (см. пример 1 в § 3.1).

Можно легко убедиться, что данный случайный процесс является центрированным, т. е. его математическое ожидание не зависит от времени и равно нулю:

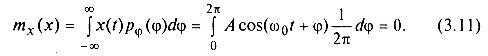
Поэтому ковариационная и корреляционная функции данного процесса совпадают и могут быть найдены следующим образом (поскольку реализации данного случайного процесса представляют собой функции, зависящие от одной случайной величины, для усреднения произведения нет нужды прибегать к двумерной плотности вероятности — достаточно воспользоваться формулой (3.5), позволяющей произвести усреднение произвольной функции от случайной величины):

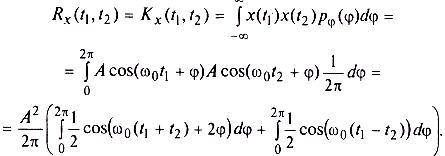
Здесь в первом слагаемом интегрирование проводится по двум периодам функции cos, поэтому данный интеграл равен нулю. Во втором слагаемом подынтегральная функция не зависит от переменной интегрирования φ, так что результат интегрирования равен произведению подынтегрального выражения и длины промежутка интегрирования, равной 2π. Окончательно получаем

Как видим, корреляционная функция данного случайного процесса гармонически зависит от расстояния между анализируемыми моментами времени. При совпадении моментов времени t₁ и t₂ получаем величину дисперсии случайного процесса:

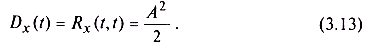
Пример 2. Рассчитаем корреляционную функцию АИМ-сигнала (см. пример 2 в § 3.1). Характеристики такого случайного процесса определяются как формой несущего импульса s_o(t), так и статистическими связями между амплитудами α_к. Часто эти амплитуды считаются статистически независимыми и имеющими идентичные вероятностные характеристики. Именно этот случай и будет рассмотрен в данном примере. Будем также считать, что эти амплитудные множители имеют нулевое математическое ожидание. При этом математическое ожидание самого случайного процесса также будет нулевым:

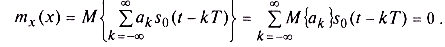
Таким образом, в данном случае ковариационная и корреляционная функции процесса также совпадают. Рассчитаем их согласно определению:

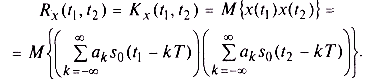
Преобразуем произведение сумм в двойную сумму и перенесем операцию статистического усреднения внутрь этой двойной суммы:

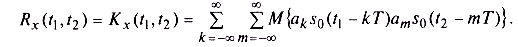
Случайными здесь являются только амплитуды а_k и а_m, поэтому и усреднение должно применяться только к ним:

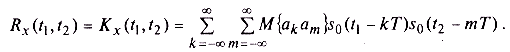
Однако согласно условиям примера эти амплитуды являются статистически независимыми и имеют нулевые средние значения. Поэтому

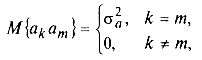
где 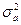— дисперсия случайных величин а_к. Таким образом,

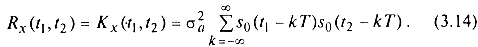
Как видим, корреляционная функция данного процесса определяется формой импульса s_o(t) и дисперсией амплитуд этих импульсов 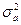. Рассчитаем дисперсию случайного процесса:

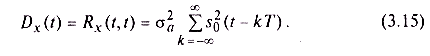
Некоррелированность и статистическая независимость. Если совместно рассматривать две случайные величины Х₁ и X₂, между ними может существовать либо не существовать статистическая связь. Отсутствие такой связи означает, что плотность вероятности одной случайной величины не зависит от того, какое значение принимает другая случайная величина. Двумерная плотность вероятности при этом представляет собой произведение одномерных плотностей:

Это условие называется условием статистической независимости.

При наличии статистической связи между случайными величинами статистические свойства каждой из них зависят от значения, принимаемого другой случайной величиной. Эта связь может быть сильной или слабой, линейной или нелинейной. Мерой линейной статистической связи между случайными величинами является коэффициент корреляции:

Можно показать, что |r₁₂| 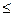1. Предельные значения ±1 достигаются, если реализации случайных величин жестко связаны линейным соотношением x₂ = аx₁ + b, где а и b — некоторые константы. Знак коэффициента корреляции при этом совпадает со знаком множителя а.

Равенство коэффициента корреляции нулю свидетельствует об отсутствии линейной статистической связи между случайными величинами (при этом говорят об их некоррелированности). Как видно из (3.16), при этом математическое ожидание произведения случайных величин равно произведению их математических ожиданий:

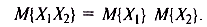
Легко показать, что из статистической независимости следует некоррелированность случайных величин. Обратное утверждение в общем случае неверно — некоррелированные случайные величины могут быть зависимыми.

Замечание 2

Классическим примером этого является пара случайных величин x₁= cos φ и x₂ =sinφ, где φ— случайная величина, равномерно распределенная на интервале О...2π. Очевидно, что х₁ и x₂ зависят друг от друга; однако их коэффициент корреляции оказывается равным нулю.

3.4. СТАЦИОНАРНЫЕ И ЭРГОДИЧЕСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Стационарные случайные процессы. Так принято называть случайные процессы, статистические характеристики которых одинаковы во всех временных сечениях.

Говорят, что случайный процесс строго стационарен (или стационарен в узком смысле), если его многомерная плотность вероятности p(x₁,x2,…,x_n ,t₁,…,t_n)

произвольной размерности n не изменяется при одновременном сдвиге всех временных сечений t₁, t₂, ..., t_n вдоль оси времени на одинаковую величину τ:

при любом τ.

Если же ограничить требования тем, чтобы от временного сдвига не зависели лишь одномерная и двумерная плотности вероятности, то такой случайный процесс будет стационарен в широком смысле. Понятно, что из стационарности в узком смысле следует

стационарность в широком смысле, но не наоборот.

Для стационарного случайного процесса математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит не от самих моментов времени, а только от интервала между ними τ = t₂ — t₁.

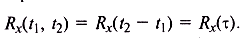
По этой причине при записи статистических параметров стационарного случайного процесса можно опускать обозначения фиксированных моментов времени: m_х, D_x, K_x(τ), R_x(τ).

Легко убедиться, что корреляционная функция стационарного случайного процесса является четной:

Кроме того, абсолютные значения этой функции при любых т не превышают ее значения при τ = 0 (напомним, что это значение равно дисперсии случайного процесса):

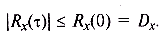
Часто удобно использовать коэффициент корреляции (его также называют нормированной корреляционной функцией)

Для коэффициента корреляции выполняются соотношения г_х(0)=1и .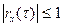

Функции R_x(τ) и г_х(τ) характеризуют связь (корреляцию) между значениями X(t), разделенными промежутком τ. Чем медленнее убывают эти функции с ростом абсолютного значения τ, тем больше промежуток, в течение которого наблюдается статистическая связь между мгновенными значениями случайного процесса, и тем медленнее, плавнее изменяются во времени его реализации.

Пример 1. Легко видеть, что гармонический случайный процесс со случайной начальной фазой (см. пример 1 в § 3.1 и вычисление характеристик этого процесса в примере 1 § 3.3) является стационарным в широком смысле. Действительно, зависящие от одномерной плотности вероятности математическое ожидание (3.11) и дисперсия (3.13) не зависят от времени, а корреляционная функция (3.12), зависящая от двумерной плотности вероятности, зависит лишь от интервала между рассматриваемыми моментами времени:

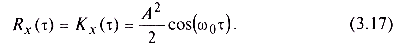
Коэффициент корреляции такого случайного процесса равен

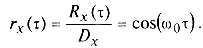
Замечание 1

Здесь следует отметить, что стационарным будет любой случайный процесс, реализации которого являются периодическими функциями, идентичными по форме и различающимися лишь «начальной фазой», т. е. положением начала отсчета времени в пределах периода. При этом принципиальной является равномерность распределения начальной фазы в пределах периода. Действительно, пусть у гармонического процесса начальная фаза равномерно распределена в пределах половины окружности — на интервале O...π. Математическое ожидание процесса в этом случае будет равно

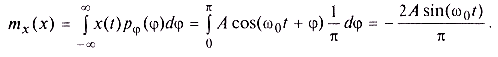
Результат вычислений показывает, что математическое ожидание процесса зависит от времени, следовательно, он не является стационарным.

Пример 2. АИМ-сигнал (см. пример 2 в § 3.1 и вычисление характеристик этого процесса в примере 2 § 3.3), очевидно, не является стационарным, поскольку его дисперсия (3.15) зависит от времени, а корреляционная функция (3.14) зависит не от расстояния между моментами времени, а от двух моментов времени по отдельности.

Эргодические случайные процессы. Дальнейшее упрощение анализа случайных процессов достигается при использовании условия эргодичности процесса. Стационарный случайный процесс называется эргодическим, если при определении любых его статистических характеристик усреднение по множеству (ансамблю) реализаций эквивалентно усреднению по времени одной, теоретически бесконечно длинной, реализации.

Обозначив усреднение по времени угловыми скобками, можно записать следующие выражения, позволяющие вычислить важнейшие статистические характеристики эргодического случайного процесса по его единственной реализации x(t) (еще раз обращаем внимание на то, что эргодический случайный процесс обязательно является и стационарным, но не наоборот):

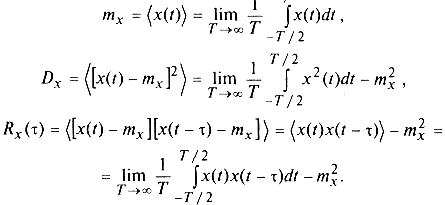
Математическое ожидание эргодического случайного процесса равно постоянной составляющей любой его реализации, а дисперсия имеет наглядный физический смысл мощности флуктуационного компонента.

Достаточным условием эргодичности случайного процесса, стационарного в широком смысле, является стремление к нулю его функции корреляции с ростом временного сдвига τ:

При экспериментальном исследовании случайных процессов доступно, как правило, наблюдение одной реализации сигнала, а не всего ансамбля. Если изучаемый процесс является эргодическим, то его реализация достаточной длины является «типичным» представителем статистического ансамбля. Согласно приведенным выше формулам по этой единственной реализации можно определить математическое ожидание, дисперсию и корреляционную функцию эргодического случайного процесса. На практике интегрирование выполняется, естественно, не в бесконечных пределах, а на конечном интервале Т, длина которого должна быть тем больше, чем выше требования к точности результатов измерения.

Пример 3. Проверим эргодичность гармонического процесса со случайной начальной фазой (стационарность такого процесса была проверена ранее). Его корреляционная функция (3.17) с ростом т не стремится к нулю, так что условие (3.18) не выполняется. Однако это лишь достаточное, но не необходимое условие, поэтому его невыполнение еще не означает неэргодичности процесса. Проверим эргодичность согласно определению, вычислив усредненные по времени параметры:

Замечание 2

Тот факт, что реализации рассматриваемого процесса являются периодическими функциями, позволяет упростить вычисления, заменив усреднение по бесконечному (в пределе) промежутку времени усреднением по одному периоду, равному в данном случае 2 π/ω₀.

Итак, параметры, вычисленные усреднением по времени, совпали с параметрами, полученными ранее путем статистического усреднения. Следовательно, гармонический случайный процесс со случайной начальной фазой является эргодическим.

Замечание 3

Здесь также следует отметить, что любой случайный процесс, реализации которого являются периодическими функциями, идентичными по форме и различающимися лишь «начальной фазой», будет не только стационарным, но и эргодическим.

Нормальный случайный процесс. Нормальный (гауссовский) закон распределения случайных величин очень удобен для анализа и часто встречается на практике, особенно он характерен для помех канала связи. Одномерная плотность вероятности стационарного нормального процесса определяется выражением

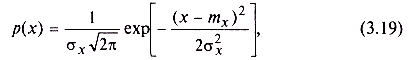
где m_х и 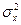— соответственно математическое ожидание и дисперсия процесса.

На рис. 3.6 приведен график плотности вероятности нормальной случайной величины, построенный согласно (3.19) при m_х = 0 и σ_x= 1.

Широкое распространение нормального закона распределения в природе объясняется тем, что при суммировании достаточно большого числа равномощных статистически независимых случайных величин, имеющих произвольные плотности распределения вероятности, плотность распределения суммы стремится к нормальной. Это положение носит название центральной предельной теоремы.

Весьма полезным для математического анализа свойством нормального распределения является то, что из некоррелированности гауссовых случайных величин следует их статистическая независимость (о разнице между этими понятиями см. § 3.3).

Замечание 4

Рис. 3.6. Плотность вероятности случайной величины с нормальным распределением

Следует обратить внимание на то, что данные распределении вероятности не дают никаких сведений о поведении случайного процесса во времени. Для описания его временных характеристик необходимо использовать корреляционную функцию или привлечь для этого спектральные характеристики случайного процесса, которые рассматриваются в § 3.5.

3.5. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Каждая отдельно взятая реализация случайного процесса представляет собой детерминированную функцию, и к ней можно применить преобразование Фурье. При этом различные реализации будут, естественно, иметь различные спектры. Нас же интересуют статистически усредненные характеристики случайных процессов. Попытаемся найти среднее значение спектральной плотности случайного процесса (горизонтальной чертой здесь и далее обозначается операция статистического усреднения по ансамблю реализаций):

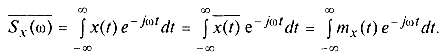
Как видно из формулы, усредненная спектральная плотность случайного процесса представляет собой спектр его детерминированной составляющей (математического ожидания). Для центрированных процессов m_x(t) = 0 и 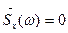. Таким образом, усредненное значение спектральной плотности не несет никакой информации о флуктуационной, т. е. собственно случайной, составляющей случайного процесса. Это говорит о том, что фазы спектральных составляющих в различных реализациях процесса случайны и независимы.

Можно, однако, рассмотреть спектральную плотность мощности случайного процесса, поскольку мощность не зависит от соотношения фаз спектральных составляющих.

Рассмотрим центрированный случайный процесс и выделим из его ансамбля какую-либо реализацию x(t), ограничив ее длительность конечным интервалом времени 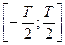. Применив затем к этой реализации прямое преобразование Фурье, найдем ее спектральную плотность 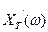. Энергию E_T рассматриваемого отрезка реализации согласно равенству Парсеваля (1.56) можно вычислить как

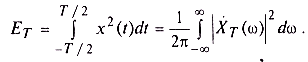
Разделив эту энергию на Т, получим среднюю мощность P_T реализации на данном временном интервале:

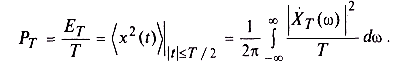
При увеличении длительности промежутка времени Т энергия отрезка реализации неограниченно возрастает, а средняя мощность стремится к некоторому пределу. Совершив предельный переход 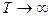, получим

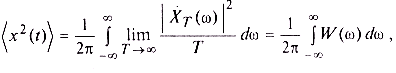
где функция

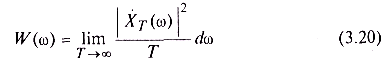
представляет собой спектральную плотность средней мощности рассматриваемой реализации.

Замечание 1

Часто говорят «спектральная плотность мощности» или «спектр мощности».

В общем случае спектральную плотность мощности W(ω) необходимо усреднить по множеству реализаций. Однако если ограничиться рассмотрением эргодических процессов, можно считать, что найденная по одной реализации (т. е. путем усреднения по времени) функция W(ω) характеризует весь процесс в целом.

Так как мы рассматриваем центрированный эргодический стационарный случайный процесс, средняя мощность любой его реализации равна дисперсии процесса. Таким образом,

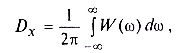
где W(ω) — вещественная функция, не содержащая информации о фазах спектральных составляющих и не позволяющая восстановить отдельные реализации случайного процесса. Кроме того, из определения спектральной плотности (3.20) очевидно, что W(ω) является неотрицательной и четной функцией частоты.

Замечание 2

Мы не приводим здесь примеров расчета спектра случайного процесса согласно приведенному определению, поскольку такого рода расчет редко необходим на практике. Как правило, вычисление спектра случайного процесса производится на основе его корреляционной функции с помощью теоремы Винера—Хинчина, речь о которой пойдет в следующем параграфе.

3.6. ТЕОРЕМА ВИНЕРА-ХИНЧИНА