Свойства нормальных делителей
Свойство 1. Подгруппа Н является нормальным делителем группы G тогда и только тогда, когда для любого xÎG и любого hÎН, xhx-1ÎН.
Доказательство. Достаточность. Пусть для всех xÎG и всех hÎН, xhx-1ÎН, где H - подгруппа группы G. Чтобы показать, что H - нормальный делитель, осталось доказать равенство xH=Нx. Пусть yÎxН, следовательно, y=xh. Умножим обе части последнего равенства на x-1 справа: yx-1=xhx-1=h1ÎН (xhx-1ÎН, по условию). Тогда yx-1=h1, умножив обе части этого равенства на х, получим yx-1x=h1x, y=h1x, то есть yÎНx. Докажите самостоятельно, что если yÎНx, то yÎхН. Таким образом, Н - нормальный делитель группы G.
Необходимость. Пусть Н - нормальный делитель группы G. Покажем, что xhx-1Î Н, для любого xÎG и для любого hÎH. Так как Н - нормальный делитель, то для любого xÎG: xH=Нx. Следовательно, xh=h1x (умножим обе части равенства на х-1): хhx-1=(h1x)x-1=h1(xx-1)=h1. Получили, что h1=хhx-1, но h1ÎН, следовательно, хhx-1 ÎН.
Свойство 2. Пусть N - нормальный делитель группы G и (а1,b1)ÎsN, (а2,b2)ÎsN , где а1,b1,а2,b2ÎG, тогда (а1а2,b1b2)ÎsN.
Доказательство. Так как (а1,b1)ÎsN то 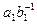 ÎN. Аналогично из того, что (а2,b2)ÎsN, следует, что
ÎN. Аналогично из того, что (а2,b2)ÎsN, следует, что 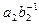 ÎN. Покажем, что (a1a2)(b1b2)-1ÎN. Действительно,
ÎN. Покажем, что (a1a2)(b1b2)-1ÎN. Действительно,
(a1a2)(b1b2)-1=a1a2 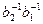 =a1a2
=a1a2 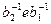 =a1a2
=a1a2 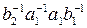 =
= 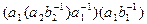 ÎN, так как
ÎN, так как 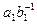 ÎN и
ÎN и 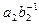 ÎN (по условию),
ÎN (по условию), 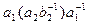 ÎN (по предыдущей теореме). Получили (a1a2)(b1b2)-1ÎN, следовательно, (а1а2,b1b2)ÎsN.
ÎN (по предыдущей теореме). Получили (a1a2)(b1b2)-1ÎN, следовательно, (а1а2,b1b2)ÎsN.
Определение. Пусть G - группа, N - нормальный делитель группы G. Фактор-группой группы G по нормальному делителю N называется множество всевозможных классов по эквивалентности sN : G/N={ 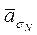 ½aÎG}.
½aÎG}.
3амечание. Для любых x,yÎG (x,y)ÎsN тогда и только тогда, когда
xy-1ÎN.
Действие в фактор-группе введено так: 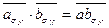 , (то есть взяв элементы а и b соответственно из классов
, (то есть взяв элементы а и b соответственно из классов 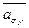 и
и 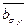 , перемножаем их, и класс, в котором окажется элемент ab, будет результатом умножения класса
, перемножаем их, и класс, в котором окажется элемент ab, будет результатом умножения класса 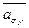 на класс
на класс 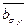 ). Элементами фактор-группы являются не отдельные элементы, а множества элементов - классы по эквивалентности s.
). Элементами фактор-группы являются не отдельные элементы, а множества элементов - классы по эквивалентности s.
Теорема. Фактор-группа является группой относительно введенного в ней алгебраического действия.
Доказательство. Пусть G - группа, N -- ее нормальный делитель.
1. Докажем, что введенное выше действие является алгебраическим. Для этого надо показать, что для каждой пары элементов из фактор-группы однозначно определено отображение в эту же фактор-группу. Каждые два элемента из факторгруппы можно перемножить, в результате получим какой-то класс, принадлежащий фактор-группе (объясните, почему?). Значит, действие всюду определено. Докажем, что оно определено однозначно. Пусть 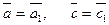 . Будут ли равны классы
. Будут ли равны классы 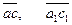 ? Да, это следует из второго свойства нормальных делителей. Таким образом, мы доказали, что определено отображение, следовательно, действие является алгебраическим.
? Да, это следует из второго свойства нормальных делителей. Таким образом, мы доказали, что определено отображение, следовательно, действие является алгебраическим.
2. Докажем, что действие ассоциативно. Возьмем произвольные элементы 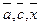 из G/N. Тогда
из G/N. Тогда 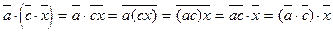 (мы воспользовались ассоциативностью в G и определением действия).
(мы воспользовались ассоциативностью в G и определением действия).
3. Найдем единицу в G/N. В группе G есть единица. При разбиении G на классы единица попадает в какой-то класс (какой именно?). Докажем, что этот класс и будет единицей в фактор-группе. Действительно, для любого элемента 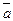 из G/N,
из G/N, 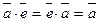 .
.
4. Покажем, что для любого элемента 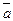 из G/N:
из G/N: 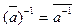 . Действительно,
. Действительно, 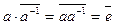 . Следовательно, фактор-группа является группой относительно введенного выше действия.
. Следовательно, фактор-группа является группой относительно введенного выше действия.
Упражнения
1. Доказать, что множество H={x½x=3q, qÎZ}, есть нормальный делитель группы Z относительно сложения. Построить фактор-группу Z/H.
2. G - циклическая группа 6-го порядка. G=[а]={е, а, а2, а3, а4, а5}.
а) найти все подгруппы группы G;
б) показать, что каждая подгруппа является нормальным делителем группы G;
в) построить фактор-группу группы G по всем нормальным делителям;
г) проверить, являются ли построенные фактор-группы циклическими группами.
3. Найти все подгруппы циклической группы 4-го порядка и фактор-группы по ним.
ГОМОМОРФИЗМЫ ГРУПП
Определение. Пусть А - множество с алгебраическим действием “·“, В - множество с алгебраическим действием “*“. Отображение j множества А во множество В называется гомоморфизмом, если для любых a1 ,a2, принадлежащих множеству А, выполняется j(а1·а2)=j(а1)*j(а2).
Пример. Рассмотрим два множества: (Â+, × ) - множество положительных вещественных чисел с введенным в нем действием умножения; (Â,+) - множество всех вещественных чисел с введенным в нем действием сложения. Примером гомоморфизма между этими множествами может служить логарифмическая функция: j: Â+®Â, где "аÎÂ+(j(а)=lga). Действительно, lg(ab)=lga + lgb.
Определение. Гомоморфизм j: (А,×) ® (В,*) называется изоморфизмом, если j является биекцией.
Определение. Пусть j: А®В. Образом множества А при отображении j называется множество Jmj={yÎB½$xÎA(j(x)=y)}.
Предложение. Пусть даны множества (А,*), (В,´), j - гомоморфизм из А в В, (А,*) - группа. Тогда образ множества А при гомоморфизме j образует группу относительно действия “´”.
План доказательства: Нам нужно показать, что Jmy - группа относительно действия “´”. Для этого докажем, что
1) “´” - алгебраическое действие на Jmj;
2) выполняется свойство ассоциативности;
3) существует единица и для каждого элемента существует обратный. Доказательство.
1. Пусть y1, y2 ÎJmj. По определению образа, у1=j(х1), y2=j(x2) для некоторых x1, x2ÎA. Покажем, что y1´y2ÎJmj: y1´y2=j(х1)´j(x2)=j(х1*x2). Так как А - группа и x1, x2ÎA, то х1*x2ÎA. Таким образом, получили, что ($xÎA)(j(x)=y1´y2, а это значит, что y1´y2 ÎJmj. Следовательно, “´” - алгебраическое действие.
2. Возьмем произвольные y1, y2, y3Î Jmj. Покажем, что (y1´y2)´y3=y1´(y2´y3). Имеем
(y1´y2)´y3=(j(х1)´j(x2))´j(х3)=j(х1*x2)´j(х3)=j((х1*x2)*х3)=j(х1*(х2*х3))=j(х1)´j(х2*х3)=j(х1)´(j(х2)´j(х3))= y1´(y2´y3). То есть действие ассоциативно.
3. Пусть е единица в A, j(e)ÎJmj. Покажем, что j(е) - единица множества Jmj. Возьмем yÎJmj, тогда ($хÎA)(j(х)=y). j(e)´y = j(e)´j(x) = j(e*x) = j(x) = y, y´j(e) = j(x)´j(e) = j(x*e) = j(x) = y. Следовательно, в Jmj есть единица. Найдем обратный элемент для произвольного yÎJmj. Пусть y = j(х). Рассмотрим j(x-1): y´j(x-1) = j(x)´j(x-1) = j(x*x-1) = j(e).
Но j(е) - единица в образе, следовательно, j(х-1) - обратный элемент для j(х)=y.
Определение. Пусть j - гомоморфизм из группы G в группу G’. Ядром гомоморфизма j называется множество Kerj={xÎG½j(x)=e’}, где е’ единица группы G’.
Предложение. Пусть j - гомоморфизм, j:G®G’, G - группа, тогда Kerj является нормальным делителем группы G.
1. Докажем, что Kеrj - подгруппа группы G. Пусть x1, x2ÎKerj, тогда j(x1)=е’, j(x2)=е’. Необходимо доказать, что j(x1x2)=е’. Действительно, j(x1x2)= j(x1)´ j(x2) =е’´ е’=e’. Значит, x1x2ÎKerj.
Осталось показать, что для произвольного хÎKerj и x-1ÎKerj. (Докажите самостоятельно.)
2. По первому свойству нормальных делителей, нужно проверить, что для произвольных хÎG и aÎKerj имеет место xax-1ÎKerj. Рассмотрим j(xax-1)= j(x)´j(а)´j(x-1)=j(x)´e’´j(x-1)=j(x)´j(x-1)=j(xx-1)=j(e)=e’. Значит, xax-1ÎKerj.
Таким образом, мы доказали, что Kerj - нормальный делитель группы G
Предложение. Пусть j:G®G’. Гомоморфизм j является изоморфизмом тогда и только тогда, когда Kerj={e}, Jmj=G’.
Доказательство. Необходимость. Пусть j - изоморфизм, докажем, что Kerj={e}, Jmj=G’. Так как j - биекция, следовательно, и сюръекция, то Jmj=G’. Для доказательства того, что Kerj={e}, необходимо показать, что еÎ Kerj={e} и KerjÌ{e}. Так как j - сюръекция, то элемент е’ имеет прообраз, обозначим его х. Он, по определению, принадлежит Kerj. Так как ядро - подгруппа, то х-1ÎKerj и xx-1 ÎKerj, но xx-1=е, следовательно, еÎKerj. Докажем теперь обратное включение. Пусть x¹e: xÎKerj. Тогда j(x)=e’ и j(e)=e’. Следовательно, j(x)=j(е), но j - инъекция, тогда x=е. Таким образом, получили Kеrj={е}, Jmj=G’.
Достаточность. Пусть Kerj={e}, Jmj=G. Докажем, что j - биекция. Из того, что Jmj=G’, следует, что j - сюръекция. Предположим, что j не является инъекцией. То есть х1¹х2, а j(х1)=j(х2). Домножим обе части этого равенства на j(х2-1), получим:
j(x2-1)´j(х1)=j(х2-1)´j(x2), j(х2-1х1)=е’, значит, x2-1x1ÎKerj, то есть x2-1x1=е, следовательно, x2=x1. Получили противоречие, следовательно, предположение неверно, то есть j - инъекция. Следовательно, j - биекция.
Схолия(теорема о гомоморфизмах групп). Пусть имеется гомоморфизм j:G®G’, Kerj - ядро, Jmj=j(G), тогда фактор-группа по ядру этого гомоморфизма изоморфна образу: G/Kеrj@Jmj.
План доказательства:
1. Установим бинарное отношение y между множествами G/Kеrj и Jmj.
2. Докажем, что y - функция, отображение, сюръекция, инъекция (то есть y - биекция).
3. Покажем, что y - гомоморфизм, то есть сохраняет алгебраическую операцию. Таким образом, мы докажем, что y - изоморфизм.
Доказательство
1. Положит y( 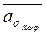 )=j(a), где
)=j(a), где 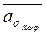 - класс смежности группы G по подгруппе Kerj, одним из элементов которого является aÎG. Это отношение y является бинарным отношением между фактор-группой G/Kеrj и Jmj, так как
- класс смежности группы G по подгруппе Kerj, одним из элементов которого является aÎG. Это отношение y является бинарным отношением между фактор-группой G/Kеrj и Jmj, так как 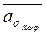 ÎG/Kеrj, а j(a)ÎJmj.
ÎG/Kеrj, а j(a)ÎJmj.
2. Покажем, что найденное бинарное отношение является биекцией. а) будет ли y - функцией: пусть 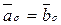 (для простоты записи вместо sKerj будем писать s). Тогда, по определению функции, нужно показать, что y(
(для простоты записи вместо sKerj будем писать s). Тогда, по определению функции, нужно показать, что y( 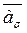 )=y(
)=y( 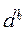 ). Так как классы
). Так как классы 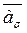 и
и 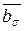 равны, то (а,b)Îs, тогда, по определению, s имеем ab-1ÎKerj, то есть j(ab-1)=
равны, то (а,b)Îs, тогда, по определению, s имеем ab-1ÎKerj, то есть j(ab-1)= 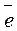 и j(a)j(b-1)=
и j(a)j(b-1)= 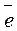 . Умножим последнее равенство на j(b), получим j(a)j(b-1)j(b)=
. Умножим последнее равенство на j(b), получим j(a)j(b-1)j(b)= 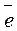 j(b), откуда j(a)=j(b). Но, по определению y: j(а)=y(
j(b), откуда j(a)=j(b). Но, по определению y: j(а)=y( 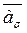 ), j(b)=y(
), j(b)=y( 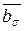 ). Следовательно, y(
). Следовательно, y( 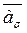 )=y(
)=y( 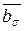 ), а это означает, что y - функция;
), а это означает, что y - функция;
б) чтобы проверить, будет ли y отображением, нужно показать, что y определено для всякого элемента из фактор-группы G/Kеrj. Пусть 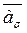 ÎG/Kеrj,
ÎG/Kеrj, 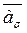 состоит из тех и только тех элементов группы G, которые находятся в отношении s. Но s - эквивалентность, следовательно, s рефлексивно. Следовательно, аÎ
состоит из тех и только тех элементов группы G, которые находятся в отношении s. Но s - эквивалентность, следовательно, s рефлексивно. Следовательно, аÎ 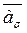 . Так как j - гомоморфизм G (он всюду определен), то определено j(а). Значит, определено и y(
. Так как j - гомоморфизм G (он всюду определен), то определено j(а). Значит, определено и y( 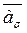 )=j(а). Доказали, что y - отображение;
)=j(а). Доказали, что y - отображение;
в) покажем, что y - инъекция. Предположим противное 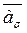 ¹
¹ 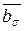 , но y(
, но y( 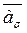 )=y(
)=y( 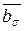 ). Так как y(
). Так как y( 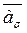 )=y(
)=y( 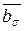 ), то j(а)=j(b). Тогда
), то j(а)=j(b). Тогда
j(a)j(b-1)=j(b)j(b-1), то есть j(ab-1)=j(bb-1)= 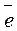 , то есть ab-1ÎKerj и (a,b)Îs, следовательно,
, то есть ab-1ÎKerj и (a,b)Îs, следовательно, 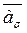 =
= 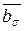 , что противоречит предположению
, что противоречит предположению 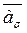 ¹
¹ 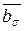 . Поэтому наше предположение неверно и y - инъекция;
. Поэтому наше предположение неверно и y - инъекция;
г) покажем, что y - сюръекция. Для этого возьмем произвольный элемент из Jmj и найдем для него прообраз. Пусть yÎJmj. Тогда существует xÎG, такой, что j(x)=y. По определению y: y( 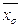 )=j(x)=y. Следовательно, y - сюръекция.
)=j(x)=y. Следовательно, y - сюръекция.
3. Покажем, что y ( 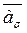
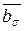 )=y(
)=y( 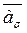 )y(
)y( 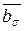 ). Действительно,
). Действительно,
y( 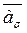
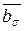 )=y(
)=y( 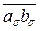 )=j(ab)=j(a)j(b)=y(
)=j(ab)=j(a)j(b)=y( 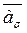 )y(
)y( 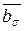 ).
).
Итак, доказали, что G/Kerj@Jmj.
Упражнение
1. Дано: G - группа, N - нормальный делитель группы G, j(а)= 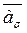 для всякого aÎG. Доказать, что j является гомоморфизмом группы G в G/N. Найти Kerj и Jmj.
для всякого aÎG. Доказать, что j является гомоморфизмом группы G в G/N. Найти Kerj и Jmj.
2. Доказать, что j: j(а)=|а| является гомоморфизмом группы Â\{0} в себя. Найти Kerj и Jmj, фактор-группу G/Kеrj, построить изоморфизм G/Kеrj®Jmj.
3. Доказать, что любая циклическая группа n-го порядка изоморфна группе корней n-ой степени из единицы относительно операции умножения.
4. Доказать, что всякая бесконечная циклическая группа изоморфна группе целых чисел относительно операции сложения.
5. G - группа несобственных квадратных матриц относительно умножения. j: j(А)=detA для всякой АÎG. Доказать, что j - гомоморфизм группы G в группу Â\{0} относительно умножения. Найти Kerj, Jmj, G/Kеr, построить изоморфизм G/Kеrj®Jmj.
6. Найти циклическую группу, порожденную матрицей 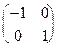 . Какой группе чисел она изоморфна?
. Какой группе чисел она изоморфна?
7. G - группа всех квадратных матриц второго порядка относительно операции сложения, j: (G,+)®(Â,+):
j 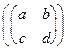 =a.
=a.
Доказать, что j - гомоморфизм. Найти Kerj, Jmj, G/Kеr, построить изоморфизм G/Kеrj®Jmj.
Дата добавления: 2020-10-25; просмотров: 225;