Разложение группы по подгруппе

Определение. Пусть Н - подгруппа группы G. Рассмотрим бинарное отношение 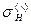на множестве G, такое, что два элемента х и y из G находятся в отношении 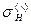тогда и только тогда, когда xy^-1ÎН.

Предложение. Отношение 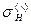- эквивалентность.

Доказательство. Необходимо показать, что 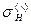обладает свойствами рефлексивности, симметричности и транзитивности. Докажем транзитивность (доказательство двух других свойств проведите самостоятельно). Пусть (x,y)Î 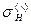и (y,z)Î 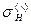, следовательно, xy^-1ÎН и yz^-1ÎН.

Так как H - подгруппа, то, перемножив элементы xy^-1 и yz^-1, получим, что xy^-1yz^-1=xz^-1ÎН, значит, (x,z)Î .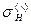

Так как 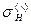- отношение эквивалентности, то оно разбивает множество Н на классы эквивалентности. Рассмотрим, как выглядят эти классы. Введем обозначение: пусть aÎG, Н - подгруппа G, Нa={x½x=ha, hÎН}.

Предложение. Пусть G - группа, Н - подгруппа G, aÎG, 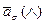- класс по эквивалентности 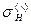, то есть это множество таких элементов, с которыми а находится в отношении 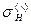. Тогда 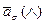=На.

Доказательство. Необходимо доказать равенство двух множеств.

1. Возьмем элемент x из 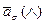и покажем, что xÎHa. Имеем xÎ 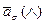, значит, (x,а)Î 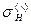, то есть xа^-1ÎН, следовательно, xа^-1=hÎН. Умножим обе части последнего равенства на а (объясните, почему можно это сделать). Получим xа^-1a =hаÎНа, то есть x=hаÎНa, значит 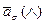ÌНа.

2. Теперь возьмем произвольный элемент xÎНa и покажем, что xÎ 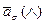. Пусть xÎНa. Это значит x=hа, следовательно, xа^-1=hÎН, то есть (x,а)Î 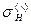, а это значит, что xÎ 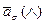. То есть На Ì .

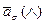Определение. Пусть G - группа, Н - подгруппа группы G, аÎG. Множество На называется левым классом смежности группы G по подгруппе Н. (Аналогично множество аН называется правым классом смежности группы G по подгруппе Н.) Сама подгруппа Н - тоже левый (правый) класс смежности, так как Н=Не=еН.

Лемма. Все левые классы смежности по подгруппе равномощны.

Доказательство. Даны два класса На и Нb. Для доказательства равномощности нужно показать, что между этими двумя классами существует биекция. Найдем отношение j между На и Нb и докажем, что оно удовлетворяет четырем свойствам биекции (то есть является отображением, функцией, сюръекцией и инъекцией). Отношение j определим следующим образом: (x,y)Îj тогда и только тогда, когда существует элемент hÎН такой, что x=ha и y=hb.

1. Докажем, что j - функция. (По определению функции, из того, что (x,y₁)Îj и (x,y₂)Îj следует, что y₁=y₂.) Рассмотрим отношение j: (x,y₁)Îj, следовательно, x=hа и y₁=hb, (x,y₂)Îj, следовательно, x=h’a и y₂=h’b, следовательно, ha=h’a, значит, h=h’ и, следовательно, y₁=y₂.

2. Докажем, что j - отображение. (По определению отображения, необходимо доказать, что D(j)=Hа.) Пусть xÎD(j), значит, существует yÎHb, что (x,y)Îj, то есть x=hа и y=hb, следовательно, xÎНа. Пусть xÎНа, следовательно, х=hа. Рассмотрим y=hb. Тогда (x,y)Îj, то есть существует yÎНb, а значит xÎD(j). Таким образом, равенство двух множеств дoказанo, а следовательно, j - отображение.

3. Докажем, что j - инъекция. (По определению инъекции, из того, что (x₁,y)Îj и (x₂,y)Îj следует, что x₁=x₂.)

Рассмотрим отношение j: (x₁,y)Îj, следовательно, x₁=ha и y=hb; (x₂,y)Îj, следовательно, x₂=h’a и y=h’b, тогда hb=h’b, значит h=h’, и поэтому x₁ =x₂.

4. Докажем, что j - сюръекция. (По определению сюръекции, необходимо доказать, что Е(j)=Нb.) Пусть yÎЕ(j), это значит, что существует xÎНа, такой что (x,y)Îj, то есть x=ha и y=hbÎНb.

Итак, в 1 - 4 доказано, что j - биекция. Следовательно, любые два класса смежности равномощны.

Теорема (Лагранжа). Пусть G - группа, Н - подгруппа группы G. Пусть G имеет мощность m, Н - мощность n, тогда m делится на n.

Доказательство. Рассмотрим разбиение группы G, соответствующее эквивалентности s. Классами по этой эквивалентности будут левые классы смежности, среди которых будет и Н. По лемме, эти классы равномощны. Значит, m=kn, kÎÀ. Следовательно, m делится на n.

Упражнения. Пользуясь определением, найти s_H:

1) G - группа целых чисел по сложению, H={x½x=3q, qÎZ};

2) G - группа вещественных чисел Â\{0} по умножению, Н={-1,1};

3) G - группа вещественных чисел Â\{0} по yмножению, H={x½x=5q, qÎZ}.