Углы между двумя прямыми, между прямой
И плоскостью
1.Пусть каждая из прямых 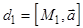 и
и 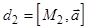 задана точкой и направляющим вектором, при этом
задана точкой и направляющим вектором, при этом
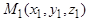 ,
, 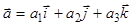
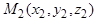 ,
, 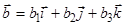 .
.
относительно системы координат 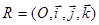 .
.
Пусть прямые 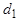 и
и 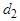 заданные в пространстве, не параллельны. Возьмем произвольную точку
заданные в пространстве, не параллельны. Возьмем произвольную точку 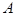 пространства и проведем через нее прямые
пространства и проведем через нее прямые 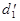 и
и 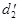 соответственно параллельные прямым
соответственно параллельные прямым 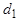 и
и 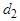 . Прямые
. Прямые 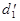 и
и 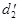 образуют четыре угла с вершиной
образуют четыре угла с вершиной 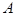 . Каждый из этих углов называется углом между прямыми
. Каждый из этих углов называется углом между прямыми 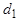 и
и 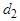 . Если известен один из четырех указанных углов, то легко определяются остальные три угла. Один из этих углов в точности угол между направляющими векторами этих прямых.
. Если известен один из четырех указанных углов, то легко определяются остальные три угла. Один из этих углов в точности угол между направляющими векторами этих прямых.
Таким образом, угол 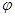 между прямыми
между прямыми 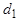 и
и 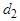 вычисляется по формуле:
вычисляется по формуле:
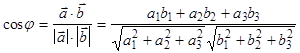
Отсюда получаем условие перпендикулярности двух прямых: ( 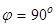 ) :
) : 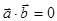 .
.
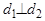
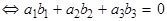
Напомним, что две взаимно перпендикулярные прямые в пространстве могут быть как скрещивающимися, так и пересекающимися.
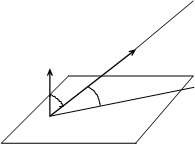
2.Если прямая 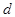 не параллельна плоскости
не параллельна плоскости  , то углом между прямой
, то углом между прямой 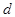 и плоскостью
и плоскостью  называется острый угол между этой прямой
называется острый угол между этой прямой 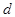 и её ортогональной проекцией
и её ортогональной проекцией 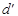 на плоскость
на плоскость  .
.
Если же прямая 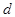 перпендикулярна плоскости
перпендикулярна плоскости  то угол между прямой и плоскостью считается равным
то угол между прямой и плоскостью считается равным 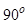 .
.
Пусть уравнения 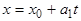 ,
, 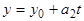 ,
, 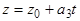 и
и 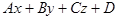 =0 определяют прямую и неперпендикулярную к ней плоскость относительно прямоугольной системы координат
=0 определяют прямую и неперпендикулярную к ней плоскость относительно прямоугольной системы координат 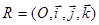 .
.
Обозначим через 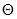 острый угол между прямой
острый угол между прямой  и её ортогональной проекцией
и её ортогональной проекцией 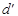 на плоскость
на плоскость  ,
, 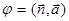 , где
, где 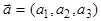 - направляющий вектор прямой
- направляющий вектор прямой 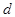 ,
,
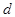
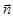
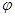 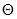 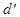

| 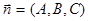 — вектор нормали плоскости — вектор нормали плоскости  .
Если угол .
Если угол 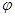 острый , то острый , то 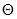 = = 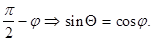 Если угол Если угол 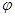 тупой, то тупой, то 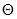 = = 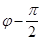 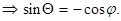
|
Таким образом,
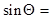
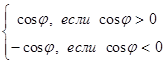
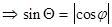 .
.
Поэтому 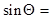
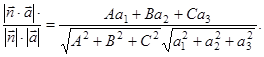
Нетрудно убедиться в том, что эта формула остается верной и в случае перпендикулярности прямой и плоскости ( когда 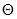 =
= 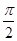 , а векторы
, а векторы 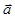 и
и 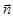 коллинераны ) .
коллинераны ) .
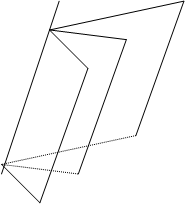
Пучок плоскостей
1.Пучкомплоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую 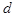 ; прямая
; прямая 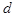 называется осью этого пучка. Пучок плоскостей с осью
называется осью этого пучка. Пучок плоскостей с осью 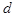 будем обозначать
будем обозначать 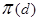 .
.
Пучок плоскостей вполне определяется заданием оси 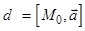 . Через любую точку
. Через любую точку 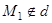 проходит единственная плоскость
проходит единственная плоскость 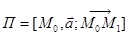 пучка
пучка 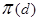 .
.
Ось пучка плоскостей 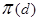 может быть задана как линия пересечения двух плоскостей пучка. Пусть известны уравнения двух различных плоскостей
может быть задана как линия пересечения двух плоскостей пучка. Пусть известны уравнения двух различных плоскостей 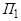 и
и 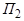 пучка
пучка 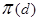
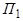 :
: 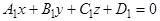 ,
, 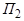 :
: 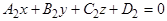
в аффинной системе координат 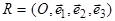 , то есть
, то есть
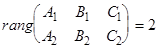 (1)
(1)
и координаты 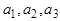 направляющего вектора
направляющего вектора 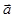 прямой
прямой 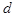 удовлетворяют условию (§13 п.4):
удовлетворяют условию (§13 п.4):
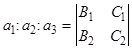 :
: 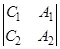 :
: 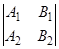 (2)
(2)
Если же 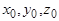 - координаты некоторой точки
- координаты некоторой точки 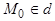
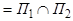 , то
, то 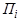 :
: 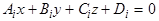 (
( 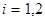 ) (3)
) (3)
Плоскость  , определяемая уравнением
, определяемая уравнением
 :
: 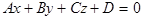 (4)
(4)
принадлежит пучку 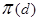 тогда и только тогда, когда
тогда и только тогда, когда
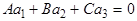 , (5)
, (5)
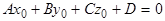 . (6)
. (6)
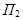

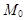 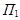
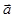
| (2),(5) 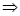 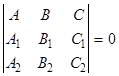 .
Отсюда, принимая во внимание (1) получаем .
Отсюда, принимая во внимание (1) получаем
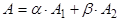 , , 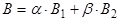 , (7) , (7)
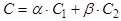 , где , где 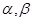 не равны нулю одновременно не равны нулю одновременно
|
Из уравнения (6) найдем 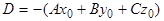 и внесем в уравнение (4), которое принимает вид:
и внесем в уравнение (4), которое принимает вид:
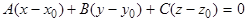
или в силу (7): 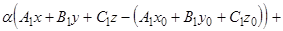
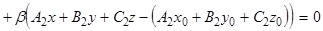
Используя равенства (3), получаем
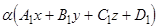
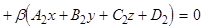 (8)
(8)
Итак, произвольная плоскость  пучка
пучка  определяется уравнением (8), и всякое уравнение вида (8) при
определяется уравнением (8), и всякое уравнение вида (8) при 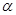 и
и 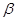 , не равных нулю одновременно, определяет плоскость пучка
, не равных нулю одновременно, определяет плоскость пучка 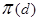 . Следовательно, уравнение (8) есть уравнение пучка
. Следовательно, уравнение (8) есть уравнение пучка 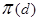 . Плоскость
. Плоскость 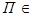
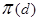 однозначно определяется заданием отношения
однозначно определяется заданием отношения 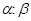 в уравнении (8).
в уравнении (8).
2.Отношение 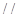 параллельности на множестве
параллельности на множестве  всех плоскостей является, очевидно, отношением эквивалентности.
всех плоскостей является, очевидно, отношением эквивалентности.
Элементы фактор-множества 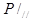 называются пучкамипараллельныхплоскостей. Следовательно, пучок параллельных плоскостей - это множество всех плоскостей, параллельных данной плоскости ( представителю этого пучка).
называются пучкамипараллельныхплоскостей. Следовательно, пучок параллельных плоскостей - это множество всех плоскостей, параллельных данной плоскости ( представителю этого пучка).
Пучок параллельных плоскостей вполне определяется заданием одной из его плоскостей
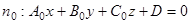 .
.
Уравнение 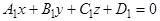 (9)
(9)
определяет произвольную плоскость этого пучка тогда и только тогда, когда 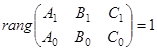
(§11) и следовательно, уравнение (9) можно представить в виде
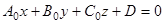 (10)
(10)
Каждому значению 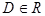 соответствует определенная плоскость рассматриваемого пучка параллельных плоскостей. Через любую точку
соответствует определенная плоскость рассматриваемого пучка параллельных плоскостей. Через любую точку 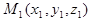 проходит единственная плоскость этого пучка; она определяется уравнением (10) при
проходит единственная плоскость этого пучка; она определяется уравнением (10) при
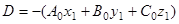
Дата добавления: 2020-10-25; просмотров: 229;










