ОБЪЕДИНЕНИЕ МНОЖЕСТВ

Объединением множеств А и В называется множество D, состоящее из тех и только тех элементов, которые принадлежат множеству А или множеству В. Символическая запись объединения множеств D=AÈB. Трудность этого определения в связке “или”, ошибка допускается в трактовке этой связки только в разделительном смысле, здесь же эта связка имеет смысл: “хотя бы в одном из…”

Примеры

1) A - множество учащихся 10-х классов школы, В - множество учащихся старших классов той же школы. Тогда AÈB - множество учащихся старших классов.

2) А - множество положительных целых чисел, В - множество, состоящее из нуля и отрицательных целых чисел, тогда AÈB - множество всех целых чисел (AÈB=Z).

3) A={1, 2, 3, 4}, À - множество всех натуральных чисел. Тогда АÈВ=À. Можно доказать, что если АÌВ, то AÈB = В.

Рассмотрим некоторые формулы:

1) АÇB=ВÇА; AÈB=BÈA;

2) АÇ(BÇC)=(АÇВ)ÇС; AÈ(BÈC)=(AÈB)ÈC;

3) АÇ(ВÈС)=(АÇВ)È(АÇС); (АÈВ)ÇС=(АÇC)È(ВÇС); AÈ(BÇC)=(AÈB)Ç(AÈC).

Для доказательства теоретико-множественных формул используются:

1) определение равенства множеств;

2) определение тех операций, которые входят в формулу;

3) если АÌB и ВÌА, то А=В (достаточное условие равенства множеств).

Докажем одну из приведенных формул: (АÈВ)ÇС=(АÇC)È(ВÇС).

Воспользуемся достаточным условием равенства множеств. Покажем, что (АÈВ)ÇС Ì (АÇC)È(ВÇС) и (АÇC)È(ВÇС) Ì (АÈВ)ÇС

1. Пусть а - произвольный элемент из (АÈВ)ÇС, тогда, по определению пересечения, aÎAÈB и аÎС, откуда, по определению объединения или аÎА и аÎС, или аÎВ и аÎС. Следовательно, аÎАÇС или аÎВÇС, и значит, аÎ(АÇC)È(ВÇС). Таким образом, мы показали, что

(АÈВ)ÇС Ì (АÇC)È(ВÇС);

2. Пусть b - произвольный элемент из (АÇC)È(ВÇС). По определению объединения, bÎ(АÇC) или bÎ(ВÇС). Тогда bÎA и bÎC или bÎB и bÎC. Отсюда bÎAÈB и bÎC, то есть bÎ(AÈB)ÇC, а значит, показано, что

(АÇC)È(ВÇС) Ì (АÈВ)ÇС.

Мы проверили достаточное условие равенства множеств. Поэтому

(АÇC)È(ВÇС) = (АÈВ)ÇС.

РАЗНОСТЬ МНОЖЕСТВ

Разностью множеств А и В называется множество D, состоящее из тех и только тех элементов, которые принадлежат множеству А и не принадлежат множеству В. Символическая запись D=A\B. Если ВÌА, то А\В называют дополнением множества В до А.

Примеры

1) Пусть А - множество всех учащихся вашей школы, в - множество девочек, учащихся в вашей школе, тогда А\В - множество мальчиков, которые учатся в вашей школе.

2) Пусть А - множество всех учащихся вашей школы, а В - множество всех учащихся соседней школы. Тогда А\В = А.

3) А=(1,2,3), В=(5,2), А\В=(1,3).

Выше было приведено интуитивное изложение элементов теории множеств. Однако теория множеств может быть построена как аксиоматическая теория. Основными понятиями аксиоматической теории множеств служат два понятия: элемент и множество, основное отношение одно: "элемент принадлежит множеству". Аксиоматики разработаны, например, Цермело и Френкелем. Приведем для примера две аксиомы.

1. Аксиома пустого множества. Существует множество, не содержащее ни одного элемента.

2. Аксиома объединения. Пусть А - множество и В - множество, тогда AÈB - множество. В дальнейшем мы будем основываться на интуитивной теории множеств.

Рассмотрим интересную задачу.

Задача о кружках. Это есть перефразировка задачи об ультрафильтрах в конечном варианте. Как научный результат, решена сравнительно недавно. С другой стороны, она была предложена на олимпиаде студентов педвузов в г. Петрозаводске в 1978 году. Ее решил студент ЛГПИ имени А. И. Герцена Тепляков Владислав. Приводим текст задачи и его решение.

В некоторой школе было n хороших учеников (Обозначим это множество М). Они занимались в 2^n-1 различных кружках. Известно, что любые 3 кружка имеют общего ученика. Доказать, что существует единственный ученик, который занимается во всех кружках.

Решение. Предварительно докажем три леммы.

Лемма 1. Пусть М содержит n элементов. Тогда множество его подмножеств Р(М) содержит 2ⁿ элементов.

Доказательство проведем методом математической индукции по n. При n=1 утверждение очевидно.

Пусть верно утверждение для фиксированного числа элементов n=k. Докажем тогда справедливость этого утверждения для n=k+1. Итак, множество М содержит k+1 элементов. Тогда множество Р(М) содержит и те элементы, которые были, то есть подмножества множества из k элементов, и новые, которые получаются из предыдущих присоединением (k+1)-го элемента. Старых подмножеств по индуктивному предположению было 2^k, тогда P(M) будет иметь 2^k+1 элементов. Лемма доказана.

Лемма 2. Пусть XÎP(M), тогда или X - кружок, или М\Х - кружок. Рассмотрим произвольное подмножество YÎP(M) и сопоставим ему в пару M\Y. Затем возьмем подмножество ZÎP(M), отличное от Y и M\Y, поставим ему в пару M\Z и т.д. Таких пар будет 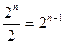, то есть столько, сколько по условию кружков. Очевидно, что в каждой паре подмножество или его дополнение есть кружок. Если бы в какой-нибудь паре не было кружка, то так как количество кружков и пар подмножеств одинаково, в некоторой паре должно быть 2 кружка, но это невозможно, так как элементы пары не пересекаются, а кружки должны пересекаться по три, а значит и по два. Возьмем произвольное подмножество ХÎP(М), тогда Х попадает в некоторую пару, а в паре есть кружок. Значит, либо х - кружок, либо М\Х - кружок.

Лемма 3. Пересечение кружков есть кружок. Пусть X и Y - кружки, а ХÇУ не является кружком. Тогда мы имеем три кружка: X, Y и М\(ХÇУ), по лемме 2, и они, по условию, должны иметь непустое пересечение. Пусть аÎ (ХÇY)Ç(М\(XÇY)), тогда аÎХÇY и аÏXÇY (по определению пересечения и дополнения). А это невозможно. Значит, пересечение кружков есть кружок.

теорема. Существует единственный элемент, принадлежащий всем кружкам.

Существование. Пусть XÇYÇZÇ...ÇT - пересечение всех кружков, тогда оно по лемме 3 - кружок, то есть это пересечение не пусто.

Единственность. Пусть два различных элемента а и b принадлежат всем кружкам. Тогда рассмотрим множество М\{а}. По лемме 2, или {а} кружок, или М\{а} кружок. Но {а} не содержит b, а М\{а} не содержит а, таким образом получили противоречие. Задача решена.