Определение многочлена

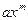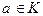Пусть K - некоторое коммутативное кольцо с единицей без делителей нуля, и пусть x - переменная. Одночленом от x с коэффициентом из K называется выражение , где , m – целое неотрицательное число. Число а называется коэффициентом одночлена, а m – степенью. Считается, что 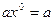, так что элементы кольца K являются одночленами нулевой степени. Выражение 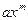рассматривается как формальная запись. Два одночлена, отличающиеся только коэффициентами, называются подобными. Для одночленов естественным образом определяются действие приведения подобных членов 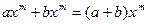и действия умножения 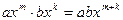. Формальное выражение, состоящее из нескольких одночленов, соединенных знаком +, называется многочленом, или многочленом от одной переменной x, заданным над кольцом K. Далее будем рассматривать только многочлены с коэффициентами из области целостности K (кольцо без делителей нуля называют областью целостности). Это всегда будет подразумеваться, даже если не будет оговорено специально.

Предполагается, что порядок следования одночленов безразличен, подобные одночлены можно соединять, а также вставлять и выбрасывать одночлены с нулевыми коэффициентами. Без нарушения общности принято считать многочлен записанным в канонической форме 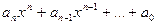(т.е. в порядке убывания степеней) или в порядке возрастания степеней .

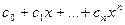Определение. Два многочлена считаются равными, если равны все коэффициенты при одинаковых степенях переменной, т.е. 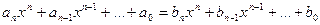в том и только в том случае, если .

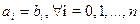Суммой двух многочленов называется многочлен, коэффициенты которого равны суммам соответствующих коэффициентов при одинаковых степенях переменной (если х^к входит только в одно слагаемое, то во втором считаем коэффициент при этой степени равным 0). Таким образом,

f(x)=a_nxⁿ+a_n-1x^n-1+…+a₁x+a₀, g(x)=b_nxⁿ+b_n-1x^n-1+…+b₁x+b₀,

f(x)+ g(x) = c_nxⁿ+c_n-1x^n-1+…+c₁x+c₀, где c_i=a_i+b_i "i=1¸n.

Например, f(x)=x³+2x²-3x+4, g(x)=3x²-6x+8, суммой f(x) и g(x) будет многочлен f(x)+ g(x)= x³+5x²-9x+12.

Произведением двух многочленов f(x) и g(x) называется многочлен h(x), коэффициенты которого вычисляются по формуле 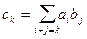. (1)

Замечание. Чтобы найти произведение двух многочленов, достаточно все члены первого сомножителя умножить на все члены второго, результаты сложить и привести подобные члены.

Пусть 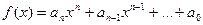, причем 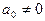. Одночлен 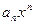называется высшим (старшим) членом многочлена f(x), и показатель n называется степенью f(x) и обозначается deg f. Нулевой многочлен не имеет высшего члена в смысле данного определения, и считается, что он равен нулю. Коэффициент а₀ называется свободным членом. Многочлен, старший коэффициент которого равен единице, называется нормированным.

Обозначим множество многочленов, заданных над областью целостности S символом S[x].

Теорема 2. Множество многочленов, заданных над областью целостности образует область целостности относительно операций сложения и умножения.

Доказательство

Из соотношения

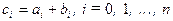(2)

легко видеть, что операция суммирования (сложения) многочленов обладает такими же свойствами, что и операция сложения элементов кольца S , т.е. ассоциативна, коммутативна; многочлен, все коэффициенты которого - нули, называется ноль-многочленом и является нейтральным элементом относительно сложения многочленов. Для каждого многочлена существует ему противоположный, противоположным к многочлену 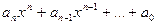является многочлен 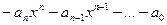. Итак, множество многочленов с операцией сложения образует коммутативную группу.

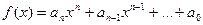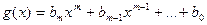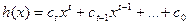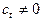Умножение многочленов ассоциативно. Это доказывается следующим образом: пусть и , , , - произвольные многочлены, тогда коэффициентом при 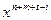, 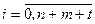в произведении 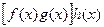будет служить элемент 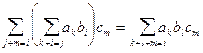, а в произведении 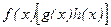- равное ему число .

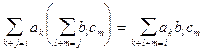Умножение многочленов дистрибутивно относительно сложения, это вытекает из равенства 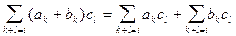, так как левая часть этого равенства является коэффициентом при 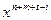в многочлене 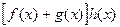, а правая часть - коэффициентом при той же степени переменной 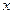в многочлене .

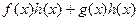Многочлен, все одночлены которого имеют 0 степень, называется многочленом нулевой степени. Очевидно, что любой элемент кольца S – многочлен 0 степени.

Нетрудно видеть, что многочлен 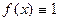(где 1 - единица кольца S) играет роль единицы при умножении многочленов. Таким образом, множество многочленов от переменной x с коэффициентами из кольца составляет кольцо по отношению к выше определенным операциям сложения и умножения многочленов (относительно сложения - это коммутативная группа; умножение ассоциативно и дистрибутивно относительно сложения; существует единичный многочлен). это кольцо коммутативно. Оно называется кольцом многочленов от переменной x над кольцом S и обозначается S [x].

При сложении многочленов 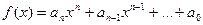и 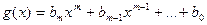по формуле (2) мы видим, что формула для суммы не содержит членов, степень которых выше, чем 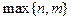, а формула (1) для произведения - членов, степень которых выше, чем n + m. Отсюда следует, что

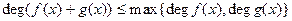, (3)

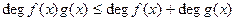. (4)

При умножении многочленов 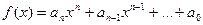степени n и 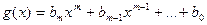степени m старший член, как следует из формулы (2), равен 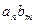(это коэффициент при 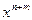). Так как в кольце нет делителей нуля, то 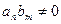, и значит, 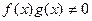. Из нашего рассуждения следует также, что

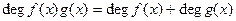. (5)

Эта формула является уточнением неравенства (4) для случая, когда в кольце S нет делителей нуля. Формула (5) также справедлива и тогда, когда один из многочленов f(x), g(x) или они оба равны нулю. Итак, произведение двух ненулевых многочленов - ненулевой многочлен.

Данное нами алгебраическое определение многочлена не содержит никакого упоминания о функциях. Тем не менее, с каждым многочленом над областью целостности S можно естественным образом связать функцию, которая определена на S и принимает значения в S.

Пусть 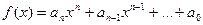- многочлен с коэффициентами из S. Для любого 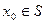положим

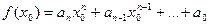, (6)

где выражение в правой части понимается как результат операций в кольце S. Получаемый при этом элемент 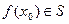называется значением многочлена f(x) при х=x₀. Таким образом, каждому элементу x₀ кольца S сопоставляется элемент f(x₀) того же кольца, и тем самым определяется функция на S со значениями в S.

Покажем, что сложение и умножение многочленов согласуются с обычными операциями, производимыми над функциями, когда складываются или, соответственно, перемножаются значения функций в каждой точке.

Рассмотрим два многочлена: 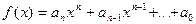, 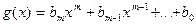. Пусть h(x) = f(x) + g(x) - их сумма. Докажем, что h(x₀)=f(x₀) + g(x₀) для любого 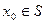. В соответствии с формулой (2)

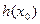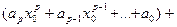
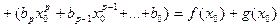= , где 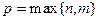, что и требовалось доказать.

Пусть теперь 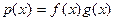- произведение многочленов f(x) и g(x). Докажем, что 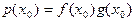для любого 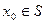. Перемножим равенства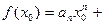 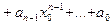, 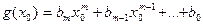. Пользуясь свойствами операций в кольце S (в частности, коммутативностью и ассоциативностью умножения), получим: 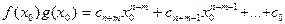, где 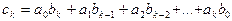. Сравнение полученного результата с формулой (2) позволяет сделать вывод, что .

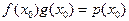Таким образом, функция, определяемая суммой (соответственно произведением) двух многочленов, есть сумма (соответственно произведение) функций, определяемых этими многочленами.

Вообще говоря, соответствие между многочленами и определяемыми ими функциями не является взаимно однозначным. Однако, если кольцо S бесконечно, то различным многочленам из кольца S[x] всегда соответствуют различные функции. Если два многочлена равны в алгебраическом смысле, то они равны и как функции, то есть они равны и в функциональном смысле. обратное утверждение в общем случае неверно. Из функционального равенства двух многочленов следует их алгебраическое равенство только в том случае, когда многочлены заданы над полем нулевой характеристики.