Свойства рядов. Необходимый признак сходимости

Теорема 1.Если у сходящегося ряда отбросить конечное число его членов, то полученный ряд также будет сходящимся. Справедливо и обратное: если сходится ряд, полученный путём отбрасывания конечного числа его членов, то и сам ряд тоже сходится.

Таким образом, сходимость ряда не меняется при отбрасывании любого конечного числа его членов.

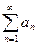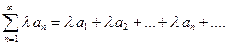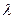Теорема 2. Пусть ряд сходится и его сумма равна S, тогда ряд , где - произвольное число, тоже сходится и его сумма равна 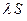. Таким образом, если все члены ряда умножить на одно и тоже отличное от нуля число, то сходимость этого ряда не изменится.

Теорема 3. Пусть ряды 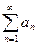и 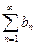сходятся, и их суммы соответственно равны S₁ и S₂. Тогда ряд 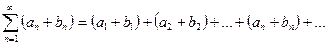так же сходится, причём его сумма равна S₁ + S₂.

Необходимый признак сходимости:

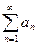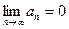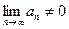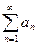Теорема Если ряд сходится, то . Таким образом, если , ряд расходится.

Доказательство:

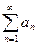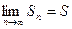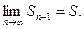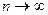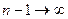Пусть ряд сходится, т.е. имеет место равенство , но тогда имеет место так же равенство Так как при и , то 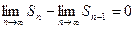, т.е. 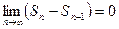. Так как 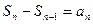, то 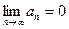, что и требовалось доказать.

Пример. Исследовать на сходимость с помощью необходимого признака:

1) 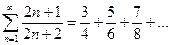, 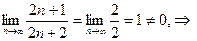ряд расходящийся.

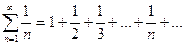
2) 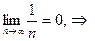ряд 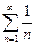возможно является сходящимся.

Вернёмся к ряду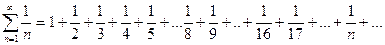

Составим рад, члены которого равны или заведомо больше, чем члены рассматриваемого ряда: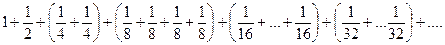

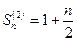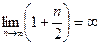, , из чего следует, что составленный нами ряд расходится. Так как 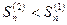, т.е. любая частичная сумма данного ряда меньше частичной суммы гармонического ряда, то и 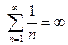, т.е. гармонический ряд – это расходящийся ряд. Следовательно, необходимый признак не является достаточным.